18.2.6 正方形的判定教学课件(共34张PPT)
文档属性
| 名称 | 18.2.6 正方形的判定教学课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 13:55:57 | ||
图片预览






文档简介
(共34张PPT)
人教版八下数学
精品同步教学课件
18.2 特殊的平行四边形
18.2.6 正方形的判定
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
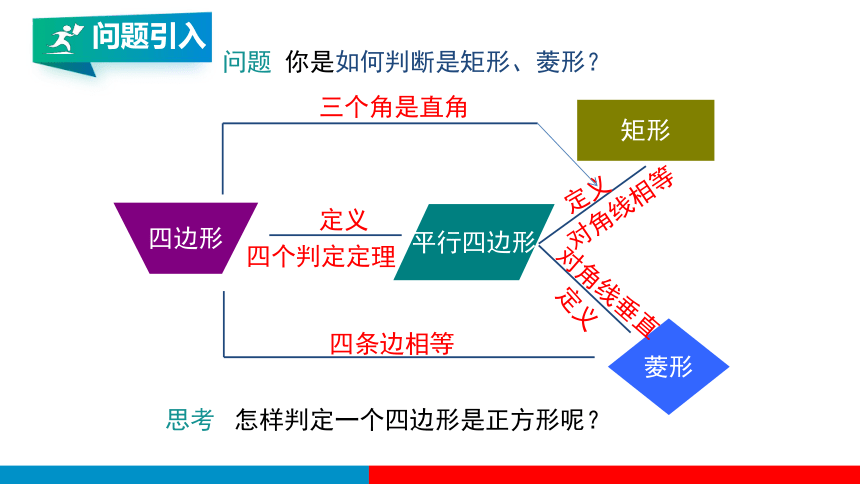
问题 你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
思考 怎样判定一个四边形是正方形呢?
问题引入
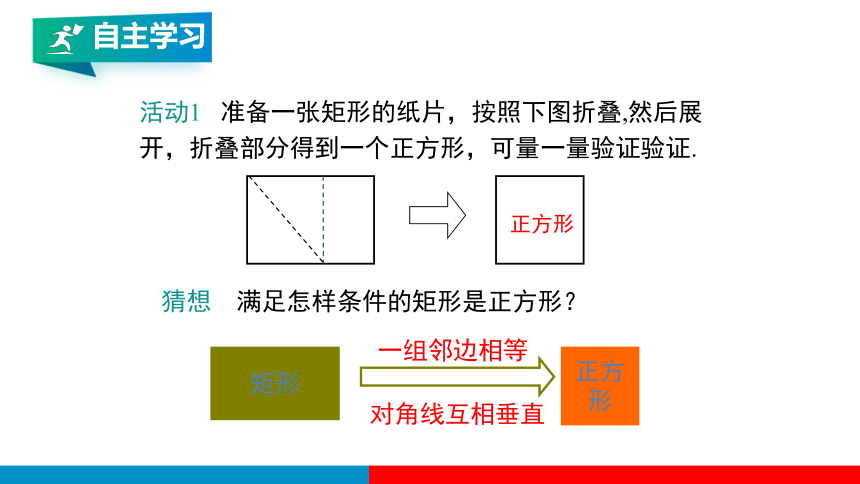
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
自主学习
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线互相垂直的矩形是正方形.
自主学习
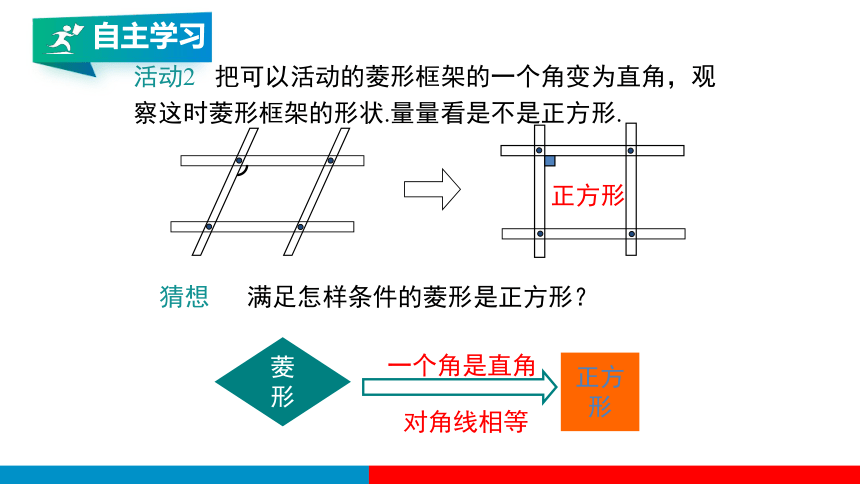
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
自主学习
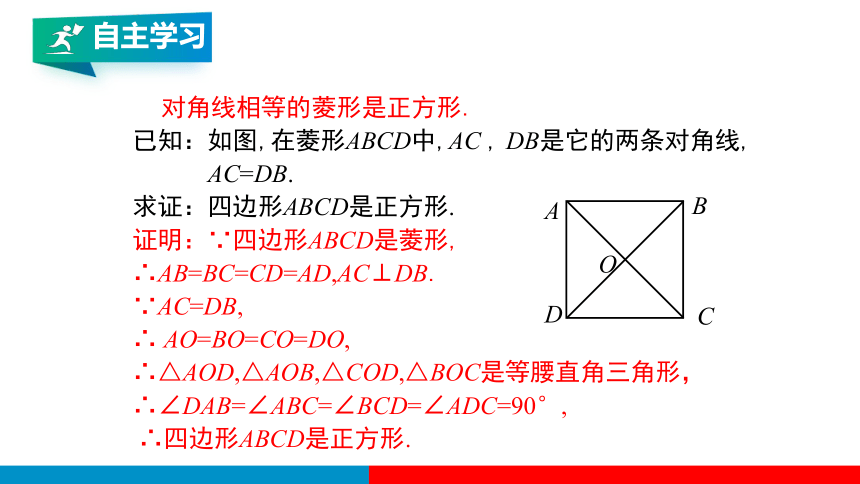
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线相等的菱形是正方形.
自主学习
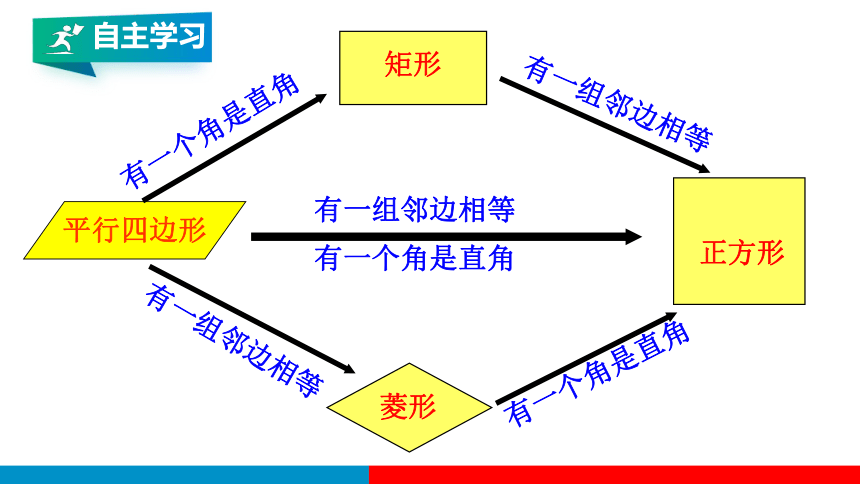
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
自主学习
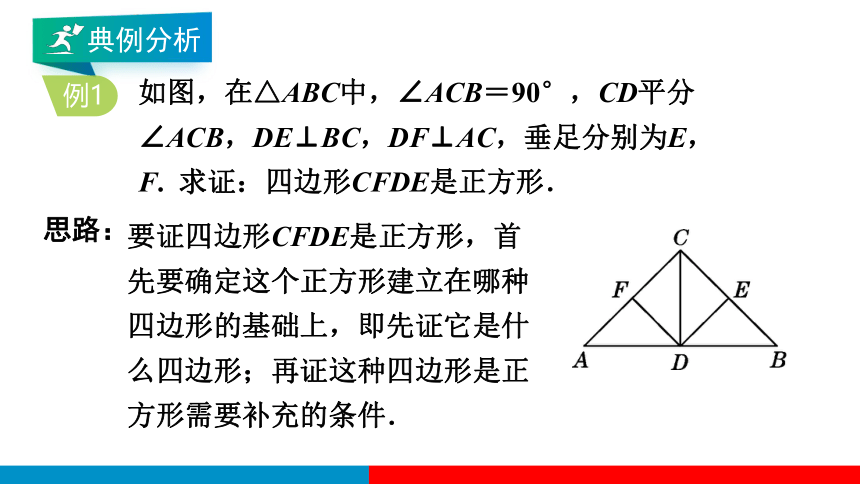
例1
思路:
如图,在△ABC中,∠ACB=90°,CD平分
∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,
F. 求证:四边形CFDE是正方形.
要证四边形CFDE是正方形,首先要确定这个正方形建立在哪种四边形的基础上,即先证它是什么四边形;再证这种四边形是正方形需要补充的条件.
典例分析
证法一:
∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE , ∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴ CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
证法二:∵∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.
典例分析
归 纳
证明条件中不含对角线的四边形是正方形的四种
方法:方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直
角”;方法3:证:“矩形+一组邻边相等”;方法4:
证:“菱形+一个直角”.
例2 在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
分析:由已知可证△AEN≌△BFE≌
△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
典例分析
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
典例分析
例 3
如图,已知在 ABCD中,对角线AC,BD交于点O,
E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD是正方形.
要证 ABCD是正方形,有三种途径可走:即在平行四
边形、菱形、矩形的基础上,找各需补充的对角线的
条件进行证明;若要证明 ABCD是菱形,由于题中条
件与对角线相关,则需证AC⊥BD.
思路:
(1)∵四边形ABCD是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.
证明:
典例分析
归 纳
证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
1.
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形
(1)是;(2)是;(3)是;(4)是.原因略.
解:
课堂练习
2.
如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件___________________________,使四边形ABCD是正方形.
∠BAD=90°(答案不唯一)
课堂练习
3.
下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正
方形
D
课堂练习
4.
在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,AD,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形;
②如果EF⊥AD,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
B
课堂练习
5.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(1) 求证: ADB= CDB;
(2) 若 ADC=90 ,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵BD平分∠ABC.
∴∠1=∠2.
又∵AB = BC,
∴△ABD≌△CBD (SAS).
∴∠ADB=∠CDB.
1
2
课堂练习
C
A
B
D
P
M
N
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形NPMD是矩形.
∵∠ADB=∠CDB,
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
课堂练习
6.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由;
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
∴当AD平分∠BAC时,四边形AEDF为菱形.
课堂练习
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
解:由四边形AEDF为正方形,
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
课堂练习
7. 如图,正方形ABCD中,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),
问四边形AFBE是什么特殊四边形?说明理由.
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB ,∠DAE=∠BAF ,AE=AF ,
∴△ADE≌△ABF(SAS),∴BF=DE.
(2)解:当点E运动到AC的中点时,四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE= AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴四边形AFBE是平行四边形,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
正方形及其性质
5种识别方法
三个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
正方形
(1) 如下图(1),四边形OBCD是矩形,O,B,D三点
的坐标分别是(0,0),(b,0),(0,d). 求点C的坐
标.
1.
解:(1) ∵四边形OBCD是矩形,
∴∠CDO=∠CBO=90°,
CD=OB=b,CB=DO=d.
∴点C的坐标为(b,d).
备选习题
如下图(2),四边形ABCD是菱形,C,D两点的坐标分别是(c,0),(0,d),点A,B在坐标轴上.求A,B两点的坐标.
(2)
(2) ∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,
OB=OD.
∴A(-c,0),B(0,-d).
备选习题
如下图(3),四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,d). 求B,C两点的坐标.
(3)
(3) ∵四边形OBCD是正方形,
∴∠CDO=∠CBO=90°,
OB=BC=CD=DO=d.
∴B(d,0),C(d,d).
备选习题
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN. 试判断四边形EFMN是什么图形,并证明你的结论.
2.
解:四边形EFMN是正方形.
证明如下:∵四边形ABCD是正方形,
∴AB=BC=CD=DA.
又∵AE=BF=CM=DN,
∴BE=CF=DM=AN.
备选习题
由勾股定理可得,EF=FM=MN=EN.
∴四边形EFMN是菱形.
易证△NAE≌△EBF,
∴∠ANE=∠BEF.
∵∠ANE+∠AEN=90°,
∴∠BEF+∠AEN=90°.
∴∠NEF=90°.
∴四边形EFMN是正方形.
备选习题
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
18.2 特殊的平行四边形
18.2.6 正方形的判定
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
问题 你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
思考 怎样判定一个四边形是正方形呢?
问题引入
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
自主学习
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线互相垂直的矩形是正方形.
自主学习
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
自主学习
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线相等的菱形是正方形.
自主学习
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
自主学习
例1
思路:
如图,在△ABC中,∠ACB=90°,CD平分
∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,
F. 求证:四边形CFDE是正方形.
要证四边形CFDE是正方形,首先要确定这个正方形建立在哪种四边形的基础上,即先证它是什么四边形;再证这种四边形是正方形需要补充的条件.
典例分析
证法一:
∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE , ∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴ CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
证法二:∵∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.
典例分析
归 纳
证明条件中不含对角线的四边形是正方形的四种
方法:方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直
角”;方法3:证:“矩形+一组邻边相等”;方法4:
证:“菱形+一个直角”.
例2 在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
分析:由已知可证△AEN≌△BFE≌
△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
典例分析
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
典例分析
例 3
如图,已知在 ABCD中,对角线AC,BD交于点O,
E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD是正方形.
要证 ABCD是正方形,有三种途径可走:即在平行四
边形、菱形、矩形的基础上,找各需补充的对角线的
条件进行证明;若要证明 ABCD是菱形,由于题中条
件与对角线相关,则需证AC⊥BD.
思路:
(1)∵四边形ABCD是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.
证明:
典例分析
归 纳
证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
1.
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形
(1)是;(2)是;(3)是;(4)是.原因略.
解:
课堂练习
2.
如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件___________________________,使四边形ABCD是正方形.
∠BAD=90°(答案不唯一)
课堂练习
3.
下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正
方形
D
课堂练习
4.
在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,AD,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形;
②如果EF⊥AD,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
B
课堂练习
5.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(1) 求证: ADB= CDB;
(2) 若 ADC=90 ,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵BD平分∠ABC.
∴∠1=∠2.
又∵AB = BC,
∴△ABD≌△CBD (SAS).
∴∠ADB=∠CDB.
1
2
课堂练习
C
A
B
D
P
M
N
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形NPMD是矩形.
∵∠ADB=∠CDB,
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
课堂练习
6.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由;
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
∴当AD平分∠BAC时,四边形AEDF为菱形.
课堂练习
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
解:由四边形AEDF为正方形,
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
课堂练习
7. 如图,正方形ABCD中,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),
问四边形AFBE是什么特殊四边形?说明理由.
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB ,∠DAE=∠BAF ,AE=AF ,
∴△ADE≌△ABF(SAS),∴BF=DE.
(2)解:当点E运动到AC的中点时,四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE= AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴四边形AFBE是平行四边形,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
正方形及其性质
5种识别方法
三个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
正方形
(1) 如下图(1),四边形OBCD是矩形,O,B,D三点
的坐标分别是(0,0),(b,0),(0,d). 求点C的坐
标.
1.
解:(1) ∵四边形OBCD是矩形,
∴∠CDO=∠CBO=90°,
CD=OB=b,CB=DO=d.
∴点C的坐标为(b,d).
备选习题
如下图(2),四边形ABCD是菱形,C,D两点的坐标分别是(c,0),(0,d),点A,B在坐标轴上.求A,B两点的坐标.
(2)
(2) ∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,
OB=OD.
∴A(-c,0),B(0,-d).
备选习题
如下图(3),四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,d). 求B,C两点的坐标.
(3)
(3) ∵四边形OBCD是正方形,
∴∠CDO=∠CBO=90°,
OB=BC=CD=DO=d.
∴B(d,0),C(d,d).
备选习题
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN. 试判断四边形EFMN是什么图形,并证明你的结论.
2.
解:四边形EFMN是正方形.
证明如下:∵四边形ABCD是正方形,
∴AB=BC=CD=DA.
又∵AE=BF=CM=DN,
∴BE=CF=DM=AN.
备选习题
由勾股定理可得,EF=FM=MN=EN.
∴四边形EFMN是菱形.
易证△NAE≌△EBF,
∴∠ANE=∠BEF.
∵∠ANE+∠AEN=90°,
∴∠BEF+∠AEN=90°.
∴∠NEF=90°.
∴四边形EFMN是正方形.
备选习题
https://www.21cnjy.com/help/help_extract.php
