2021—2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质与判定同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质与判定同步达标测试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 404.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 12:11:45 | ||
图片预览

文档简介
2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》同步达标测试题(附答案)
一.选择题(共10小题,满分30分)
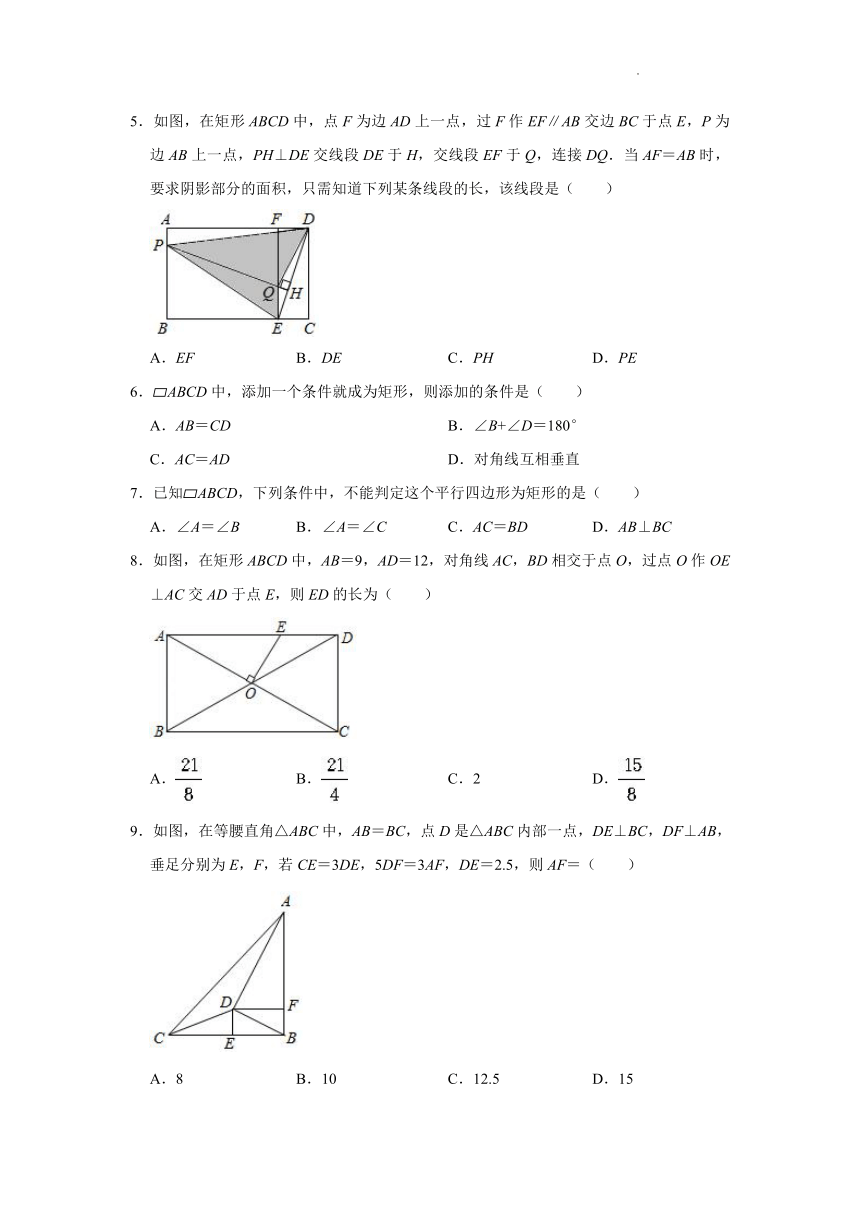
1.如图,矩形ABCD中,对角线AC,BD相交于点O,若∠OAD=40°,则∠COD=( )
A.20° B.40° C.80° D.100°
2.如图,在矩形ABCD中,对角线AC与BD相交于点O,EO⊥AC于点O,交BC于点E,若△ABE的周长为5,AB=2,则AD的长为( )
A.2 B.2.5 C.3 D.4
3.矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,连接AG,取AG的中点H,连接EH.若AB=CF=4,BC=CE=2,则EH=( )
A. B.2 C. D.
4.如图,矩形ABCD中,AE平分∠BAD交BC于点E,连接DE,若CD=3,DE=5,则AD的长是( )
A.6 B.7 C.8 D.10
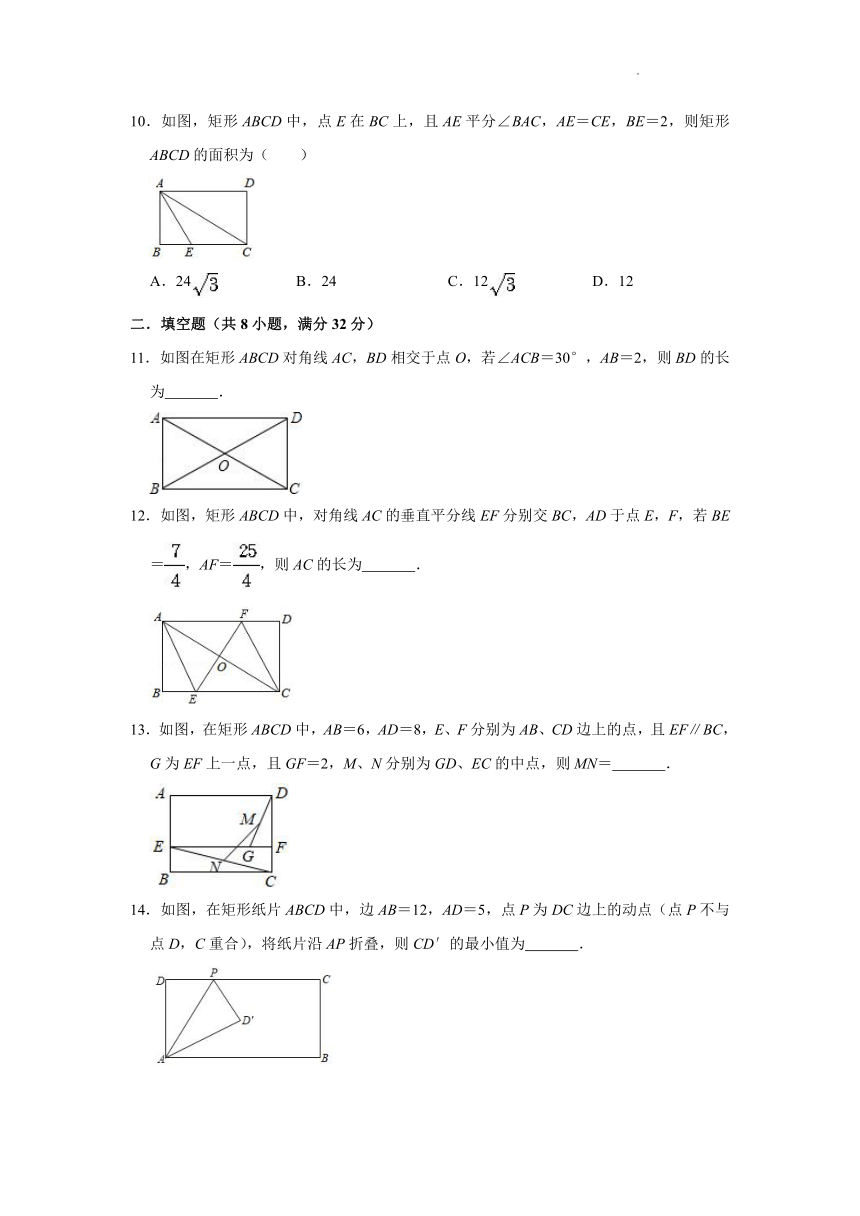
5.如图,在矩形ABCD中,点F为边AD上一点,过F作EF∥AB交边BC于点E,P为边AB上一点,PH⊥DE交线段DE于H,交线段EF于Q,连接DQ.当AF=AB时,要求阴影部分的面积,只需知道下列某条线段的长,该线段是( )
A.EF B.DE C.PH D.PE
6. ABCD中,添加一个条件就成为矩形,则添加的条件是( )
A.AB=CD B.∠B+∠D=180°
C.AC=AD D.对角线互相垂直
7.已知 ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
8.如图,在矩形ABCD中,AB=9,AD=12,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E,则ED的长为( )
A. B. C.2 D.
9.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
10.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
二.填空题(共8小题,满分32分)
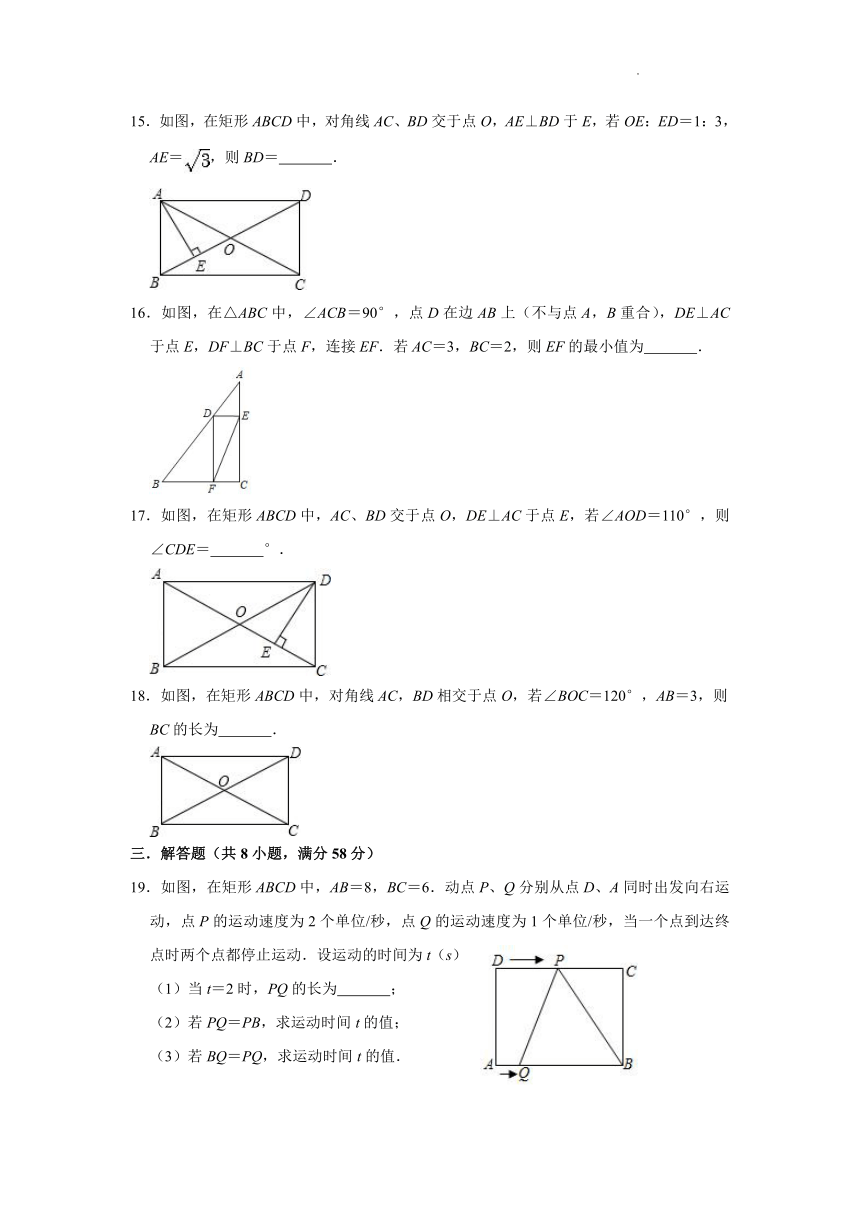
11.如图在矩形ABCD对角线AC,BD相交于点O,若∠ACB=30°,AB=2,则BD的长为 .
12.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=,AF=,则AC的长为 .
13.如图,在矩形ABCD中,AB=6,AD=8,E、F分别为AB、CD边上的点,且EF∥BC,G为EF上一点,且GF=2,M、N分别为GD、EC的中点,则MN= .
14.如图,在矩形纸片ABCD中,边AB=12,AD=5,点P为DC边上的动点(点P不与点D,C重合),将纸片沿AP折叠,则CD′的最小值为 .
15.如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若OE:ED=1:3,AE=,则BD= .
16.如图,在△ABC中,∠ACB=90°,点D在边AB上(不与点A,B重合),DE⊥AC于点E,DF⊥BC于点F,连接EF.若AC=3,BC=2,则EF的最小值为 .
17.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE= °.
18.如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠BOC=120°,AB=3,则BC的长为 .
三.解答题(共8小题,满分58分)
19.如图,在矩形ABCD中,AB=8,BC=6.动点P、Q分别从点D、A同时出发向右运动,点P的运动速度为2个单位/秒,点Q的运动速度为1个单位/秒,当一个点到达终点时两个点都停止运动.设运动的时间为t(s)
(1)当t=2时,PQ的长为 ;
(2)若PQ=PB,求运动时间t的值;
(3)若BQ=PQ,求运动时间t的值.
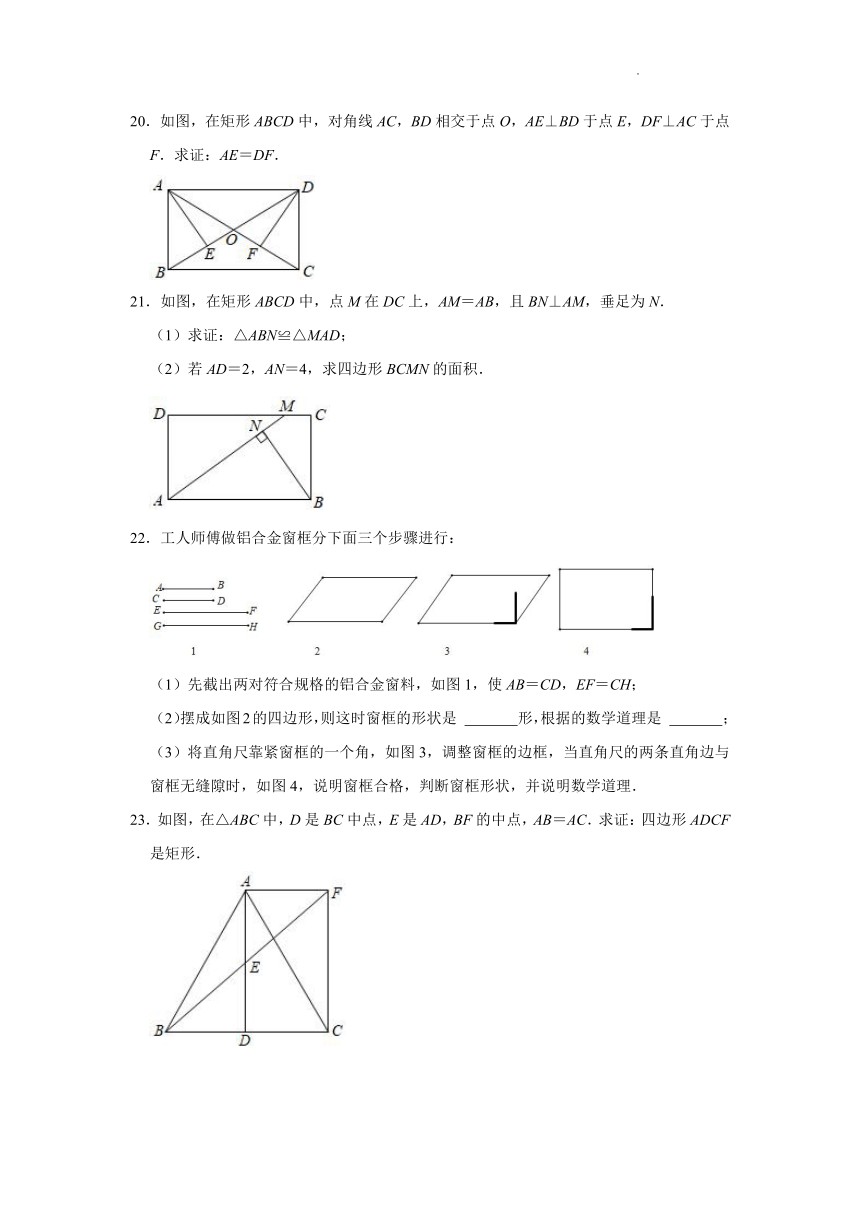
20.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F.求证:AE=DF.
21.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD;
(2)若AD=2,AN=4,求四边形BCMN的面积.
22.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图1,使AB=CD,EF=CH;
(2)摆成如图2的四边形,则这时窗框的形状是 形,根据的数学道理是 ;
(3)将直角尺靠紧窗框的一个角,如图3,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图4,说明窗框合格,判断窗框形状,并说明数学道理.
23.如图,在△ABC中,D是BC中点,E是AD,BF的中点,AB=AC.求证:四边形ADCF是矩形.
24.如图,在 ABCD中,延长AB到点E,使BE=AB,DE交BC于点O,连接EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=40°,当∠BOD等于多少度时四边形BECD是矩形,并说明理由.
25.如图,矩形ABCD中,AB=2,BC=3,点E射线BC上一动点,△ABE关于AE的轴对称图形为△FAE.
(1)当点F在对角线AC上时,求FC的长;
(2)当△FCE是直角三角形时,求BE的长.
26.已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:∠1=∠2;
(2)求证:△ADC≌△ECD;
(3)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴OD=OB=OA=OC,
∵∠OAD=40°,
∴∠ODA=∠OAD=40°,
∴∠COD=∠ODA+∠OAD=40°+40°=80°,
故选:C.
2.解:∵四边形ABCD是矩形,
∴AO=CO,BC=AD,
∵EO⊥AC,
∴AE=EC,
∵△ABE的周长为5,
∴AB+AE+BE=5,
∴2+BC=5,
∴BC=3=AD,
故选:C.
3.解:连接DH,并延长交EG于N,
∵AD∥EG,
∴∠DAH=∠AGN,
∵点H是AG的中点,
∴AH=HG,
在△ADH和△GNH中,
,
∴△ADH≌△GNH(ASA),
∴DH=HN,NG=AD=2,
∵AB=CD=EG=4,BC=CE=2,
∴DE=EN=2,
又∵∠DEN=90°,
∴DN=DE=2,
∵DE=EN,DH=HN,∠DEN=90°,
∴EH=DN=,
故选:A.
4.解:∵四边形ABCD是矩形,
∴∠C=90°,AB=CD,AD∥BC,AD=BC,
∵ED=5,CD=3,
∴EC2=DE2﹣CD2=25﹣9=16,
∴CE=4,
∵AD∥BC,
∴∠AEB=∠DAE;
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=CD=3,
∴BC=BE+EC=7,
∴AD=7,
故选:B.
5.解:过点P作PM⊥EF于点M,如图:
∵四边形ABCD为矩形,
∴AB∥DC,AD∥BC,∠C=90°,
∵EF∥AB,
∴EF∥DC,
∴∠EDC=∠DEF,
∵PH⊥DE,PM⊥EF,
∴∠PMQ=∠EHQ=90°,
又∵∠PQM=∠EQH,
∴∠QPM=∠DEF=∠EDC,
在△PMQ和△DCE中,
,
∴△PMQ≌△DCE(ASA),
∴PQ=DE,
∴阴影部分的面积=S△PDE﹣S△QED=×DE×PH﹣DE×QH=DE2,
∴故选:B.
6.解:A、当AB=CD,不能判定 ABCD为矩形,故该选项不符合题意;
B、∵ ABCD中∠B=∠D,∠B+∠D=180°,
∴∠B=∠D=90°,
∴ ABCD是矩形;故该选项正确,符合题意;
C、∵AC=AD,不能得出 ABCD是矩形,故该选项不符合题意;
D、对角线互相垂直的平行四边形是菱形,故该选项不符合题意.
故选:B.
7.解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD为矩形,故选项A不符合题意;
B、∠A=∠C不能判定 ABCD为矩形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD是矩形,故选项C不符合题意;
D、∵AB⊥BC,
∴∠B=90°,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
8.解:连接EC,如图,
∵四边形ABCD是矩形,
∴AO=OC.
∵EO⊥AC,
∴OE为线段AC的垂直平分线.
∴EC=AE.
设DE=x,则AE=12﹣x.
∴EC=12﹣x,
在Rt△ECD中,
∵EC2=DE2+DC2,
∴(12﹣x)2=x2+92.
解得:x=.
∴DE=.
故选:A.
9.解:∵DE⊥BC,DF⊥AB,
∴∠DEB=∠DFB=90°,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ABC=90°,
∴四边形DEBF为矩形,
∴BF=DE=2.5,DF=EB,
设DF=3x,则EB=3x,
∵5DF=3AF,
∴AF=5x,AB=5x+2.5,
∵DE=2.5,
∴CE=3DE=7.5,
∴CB=7.5+3x,
∵AB=CB,
∴5x+2.5=7.5+3x,
解得x=2.5,
∴AF=5x=12.5,
故选:C.
10.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
二.填空题(共8小题,满分32分)
11.解:在矩形ABCD中,∠ABC=90°,
∵∠ACB=30°,AB=2,
∴AC=2AB=2×2=4,
∵四边形ABCD是矩形,
∴BD=AC=4.
故答案为:4.
12.解:∵EF是AC的垂直平分线,
∴AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE=,
∵EF是AC的垂直平分线,
∴AE=CE=,
又∵BE=,
∴BC=BE+EC=+=8,
在Rt△ABE中,
AB====6,
在Rt△ABC中,
AC===10.
故答案为:10.
13.解:如图,取DF的中点H,CF的中点Q,连接MH,NQ,过点M作MK⊥NQ于K,
∵EF∥BC,AB∥CD,
∴四边形BCFE是平行四边形,
又∵∠BCD=90°,
∴四边形BCFE是矩形,
∴EF=BC=AD=8,
∵M、N分别为GD、EC的中点,H是DF的中点,Q是CF的中点,
∴NQ=EF=4,MH=GF=1,MH∥EF,NQ∥EF,HQ=CD=3,
∴MH∥NQ,
∵KM⊥NQ,∠NQD=90°,
∴MK∥HQ,
∴四边形MHQK是平行四边形,
∴MK=3,KQ=MH=1,
∴NK=3,
∴MN=MK=3,
方法二,连接BF,连接FM并延长交AD于H,连接BH,
∵EF∥BC,AB∥CD,
∴四边形BCFE是平行四边形,
又∵∠BCD=90°,
∴四边形BCFE是矩形,
∴BN=FN,
∵AD∥EF,
∴∠ADM=∠DGF,∠DHM=∠GFM,
又∵DM=MG,
∴△DHM≌△GFM(AAS),
∴DH=GF=2,HM=FM,
∴BH=2MN,
∵AB=6,AH=AD﹣HD=6,
∴BH=6,
∴NM=3,
故答案为3.
14.解:连接AC,当点D'在AC上时,CD'有最小值,
∵四边形ABCD是矩形,AB=12,AD=5,
∴∠D=∠B=90°,AD=BC,
∴AC=,
由折叠性质得:AD=AD'=5,∠AD'P=∠D=90°,
∴CD'的最小值=AC﹣AD'=13﹣5=8,
故答案为:8.
15.解:∵四边形ABCD是矩形,
∴BD=2OA=2OD,
∵OE:ED=1:3,
∴设OE=x,ED=3x,
则OD=2x,
∵AE⊥BD,AE=,
在Rt△OEA中,根据勾股定理,得
x2+()2=(2x)2,
解得x=1,
∴BD=4.
故答案为:4.
16.解:连接CD,如图所示:
∵∠ACB=90°,AC=3,BC=2,
∴AB===,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
此时,S△ABC=BC AC=AB CD,
即 ×2×3=××CD,
解得:CD=,
∴EF=,
故答案为:.
17.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故答案为:35.
18.解:∵∠BOC=120°,
∴∠AOB=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,AO=OC,BO=DO,
∴AO=BO,
∴△AOB是等边三角形,
∴AB=AO=BO,
∵AB=3,
∴AO=3,
∴AC=2AO=6,
由勾股定理得:BC===3,
故答案为:3.
三.解答题(共8小题,满分58分)
19.解:(1)如图所示:作PH⊥AB于H,
由题意得,DP=4,AQ=2,
则QH=2,又PH=AD=6,
由勾股定理得,PQ===2,
故答案为:2;
(2)当PQ=PB时,
如图,QH=BH,
则t+2t=8,
解得,t=;
(3)当PQ=BQ时,
(2t﹣t)2+62=(8﹣t)2,
解得,t=.
20.证明:∵四边形ABCD是矩形,对角线AC,BD相交于点O,
∴OA=OC=OB=OD,
∵AE⊥BD,DF⊥AC,
∴∠AEO=∠DFO=90°,
在△AOE和△DOF中,
,
∴△AOE≌△DOF(AAS),
∴AE=DF.
21.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,
∴∠BAN=∠AMD,
∵BN⊥AM,
∴∠BNA=90°,
在△ABN和△MAD中,
,
∴△ABN≌△MAD(AAS);
(2)解:∵△ABN≌△MAD,
∴BN=AD,
∵AD=2,
∴BN=2,
又∵AN=4,
在Rt△ABN中,AB===2,
∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,
∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.
22.解:(2):如图一所示:
∵AB=CD,EF=GH,
∴四边形为平行四边形.(两组对边相等的四边形为平行四边形)
(3)如图二所示
由(2)知四边形为平行四边形,
∵∠C为直角,
∴四边形为矩形.(一个角为直角的平行四边形为矩形)
故答案为:(2)平行四边,两组对边分别相等的四边形是平行四边形;
(3)矩,有一个角是直角的平行四边形是矩形.
23.解:∵D是BC的中点,E是BF的中点,
∴DE是△BCF的中位线,
∴DE∥FC,DE=FC,
∵E是AD的中点,
∴DE=AD,
∴AD=FC,
∴四边形ADCF是平行四边形,
又∵D是BC的中点,AB=AC,
∴∠ADC=90°,
∴平行四边形ADCF是矩形.
24.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形;
(2)解:若∠A=40°,当∠BOD=80°时,四边形BECD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=40°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=80°﹣40°=40°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形.
25.解:(1)如图所示:
∵AB=2,BC=3,
∴AC==,
∵△ABE关于AE的轴对称图形为△FAE,
∴AF=AB=2,
∴FC=AC﹣AF=﹣2.
(2)当△FCE是直角三角形时,
①当∠CFE是直角时,如(1)图所示:
由题意可知点F在对角线AC上,且EF⊥AC,
设BE=x,则EF=x,
∴S△ABC=×3×2=3,
S△ABE=×2×x=x,
S△ACE=××x,
∴3=x+x,
解得:x=2﹣4.
∴BE=2﹣4.
②当∠FCE是直角时,如图所示:
∵△ABE关于AE的轴对称图形为△FAE.
∴AB=AF,BE=EF,
在Rt△ADF中,AD=3,AF=2,
∴DF===,
CF=DC﹣CE=2﹣=,
设BE=x,则EF=x,CE=3﹣x,
∴在Rt△ADF中,
EF2=CE2+CF2,
x2=(3﹣x)2+,
解得:x=2,
∴BE=EF=2;
③当E在BC延长线上时,此时∠CEF是直角,如图所示:
由题意得:BE=AB=EF=2.
④当E在BC延长线上,∠ECF=90°时,如图所示:
在Rt△ADF中,
DF====,
∴CF=3,
设BE=t,则EF=t,CE=t﹣3,
在Rt△ECF中,
∵CF2+CE2=EF2,
即(3)2+(t﹣3)2=t2,
解得:t=6,
∴BE=6.
26.(1)证明:∵AB=AC,
∴∠B=∠2,
又∵四边形ABDE是平行四边形,
∴AB∥DE,
∴∠B=∠1,
∴∠1=∠2;
(2)证明:∵四边形ABDE是平行四边形,
∴AB=ED,
∵AB=AC,
∴AC=ED,
在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(3)解:点D在BC的中点上时,四边形ADCE是矩形,理由如下:
∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长BC的中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
一.选择题(共10小题,满分30分)
1.如图,矩形ABCD中,对角线AC,BD相交于点O,若∠OAD=40°,则∠COD=( )
A.20° B.40° C.80° D.100°
2.如图,在矩形ABCD中,对角线AC与BD相交于点O,EO⊥AC于点O,交BC于点E,若△ABE的周长为5,AB=2,则AD的长为( )
A.2 B.2.5 C.3 D.4
3.矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,连接AG,取AG的中点H,连接EH.若AB=CF=4,BC=CE=2,则EH=( )
A. B.2 C. D.
4.如图,矩形ABCD中,AE平分∠BAD交BC于点E,连接DE,若CD=3,DE=5,则AD的长是( )
A.6 B.7 C.8 D.10
5.如图,在矩形ABCD中,点F为边AD上一点,过F作EF∥AB交边BC于点E,P为边AB上一点,PH⊥DE交线段DE于H,交线段EF于Q,连接DQ.当AF=AB时,要求阴影部分的面积,只需知道下列某条线段的长,该线段是( )
A.EF B.DE C.PH D.PE
6. ABCD中,添加一个条件就成为矩形,则添加的条件是( )
A.AB=CD B.∠B+∠D=180°
C.AC=AD D.对角线互相垂直
7.已知 ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
8.如图,在矩形ABCD中,AB=9,AD=12,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E,则ED的长为( )
A. B. C.2 D.
9.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
10.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
二.填空题(共8小题,满分32分)
11.如图在矩形ABCD对角线AC,BD相交于点O,若∠ACB=30°,AB=2,则BD的长为 .
12.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=,AF=,则AC的长为 .
13.如图,在矩形ABCD中,AB=6,AD=8,E、F分别为AB、CD边上的点,且EF∥BC,G为EF上一点,且GF=2,M、N分别为GD、EC的中点,则MN= .
14.如图,在矩形纸片ABCD中,边AB=12,AD=5,点P为DC边上的动点(点P不与点D,C重合),将纸片沿AP折叠,则CD′的最小值为 .
15.如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若OE:ED=1:3,AE=,则BD= .
16.如图,在△ABC中,∠ACB=90°,点D在边AB上(不与点A,B重合),DE⊥AC于点E,DF⊥BC于点F,连接EF.若AC=3,BC=2,则EF的最小值为 .
17.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE= °.
18.如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠BOC=120°,AB=3,则BC的长为 .
三.解答题(共8小题,满分58分)
19.如图,在矩形ABCD中,AB=8,BC=6.动点P、Q分别从点D、A同时出发向右运动,点P的运动速度为2个单位/秒,点Q的运动速度为1个单位/秒,当一个点到达终点时两个点都停止运动.设运动的时间为t(s)
(1)当t=2时,PQ的长为 ;
(2)若PQ=PB,求运动时间t的值;
(3)若BQ=PQ,求运动时间t的值.
20.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F.求证:AE=DF.
21.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD;
(2)若AD=2,AN=4,求四边形BCMN的面积.
22.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图1,使AB=CD,EF=CH;
(2)摆成如图2的四边形,则这时窗框的形状是 形,根据的数学道理是 ;
(3)将直角尺靠紧窗框的一个角,如图3,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图4,说明窗框合格,判断窗框形状,并说明数学道理.
23.如图,在△ABC中,D是BC中点,E是AD,BF的中点,AB=AC.求证:四边形ADCF是矩形.
24.如图,在 ABCD中,延长AB到点E,使BE=AB,DE交BC于点O,连接EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=40°,当∠BOD等于多少度时四边形BECD是矩形,并说明理由.
25.如图,矩形ABCD中,AB=2,BC=3,点E射线BC上一动点,△ABE关于AE的轴对称图形为△FAE.
(1)当点F在对角线AC上时,求FC的长;
(2)当△FCE是直角三角形时,求BE的长.
26.已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:∠1=∠2;
(2)求证:△ADC≌△ECD;
(3)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴OD=OB=OA=OC,
∵∠OAD=40°,
∴∠ODA=∠OAD=40°,
∴∠COD=∠ODA+∠OAD=40°+40°=80°,
故选:C.
2.解:∵四边形ABCD是矩形,
∴AO=CO,BC=AD,
∵EO⊥AC,
∴AE=EC,
∵△ABE的周长为5,
∴AB+AE+BE=5,
∴2+BC=5,
∴BC=3=AD,
故选:C.
3.解:连接DH,并延长交EG于N,
∵AD∥EG,
∴∠DAH=∠AGN,
∵点H是AG的中点,
∴AH=HG,
在△ADH和△GNH中,
,
∴△ADH≌△GNH(ASA),
∴DH=HN,NG=AD=2,
∵AB=CD=EG=4,BC=CE=2,
∴DE=EN=2,
又∵∠DEN=90°,
∴DN=DE=2,
∵DE=EN,DH=HN,∠DEN=90°,
∴EH=DN=,
故选:A.
4.解:∵四边形ABCD是矩形,
∴∠C=90°,AB=CD,AD∥BC,AD=BC,
∵ED=5,CD=3,
∴EC2=DE2﹣CD2=25﹣9=16,
∴CE=4,
∵AD∥BC,
∴∠AEB=∠DAE;
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=CD=3,
∴BC=BE+EC=7,
∴AD=7,
故选:B.
5.解:过点P作PM⊥EF于点M,如图:
∵四边形ABCD为矩形,
∴AB∥DC,AD∥BC,∠C=90°,
∵EF∥AB,
∴EF∥DC,
∴∠EDC=∠DEF,
∵PH⊥DE,PM⊥EF,
∴∠PMQ=∠EHQ=90°,
又∵∠PQM=∠EQH,
∴∠QPM=∠DEF=∠EDC,
在△PMQ和△DCE中,
,
∴△PMQ≌△DCE(ASA),
∴PQ=DE,
∴阴影部分的面积=S△PDE﹣S△QED=×DE×PH﹣DE×QH=DE2,
∴故选:B.
6.解:A、当AB=CD,不能判定 ABCD为矩形,故该选项不符合题意;
B、∵ ABCD中∠B=∠D,∠B+∠D=180°,
∴∠B=∠D=90°,
∴ ABCD是矩形;故该选项正确,符合题意;
C、∵AC=AD,不能得出 ABCD是矩形,故该选项不符合题意;
D、对角线互相垂直的平行四边形是菱形,故该选项不符合题意.
故选:B.
7.解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD为矩形,故选项A不符合题意;
B、∠A=∠C不能判定 ABCD为矩形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD是矩形,故选项C不符合题意;
D、∵AB⊥BC,
∴∠B=90°,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
8.解:连接EC,如图,
∵四边形ABCD是矩形,
∴AO=OC.
∵EO⊥AC,
∴OE为线段AC的垂直平分线.
∴EC=AE.
设DE=x,则AE=12﹣x.
∴EC=12﹣x,
在Rt△ECD中,
∵EC2=DE2+DC2,
∴(12﹣x)2=x2+92.
解得:x=.
∴DE=.
故选:A.
9.解:∵DE⊥BC,DF⊥AB,
∴∠DEB=∠DFB=90°,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ABC=90°,
∴四边形DEBF为矩形,
∴BF=DE=2.5,DF=EB,
设DF=3x,则EB=3x,
∵5DF=3AF,
∴AF=5x,AB=5x+2.5,
∵DE=2.5,
∴CE=3DE=7.5,
∴CB=7.5+3x,
∵AB=CB,
∴5x+2.5=7.5+3x,
解得x=2.5,
∴AF=5x=12.5,
故选:C.
10.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
二.填空题(共8小题,满分32分)
11.解:在矩形ABCD中,∠ABC=90°,
∵∠ACB=30°,AB=2,
∴AC=2AB=2×2=4,
∵四边形ABCD是矩形,
∴BD=AC=4.
故答案为:4.
12.解:∵EF是AC的垂直平分线,
∴AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE=,
∵EF是AC的垂直平分线,
∴AE=CE=,
又∵BE=,
∴BC=BE+EC=+=8,
在Rt△ABE中,
AB====6,
在Rt△ABC中,
AC===10.
故答案为:10.
13.解:如图,取DF的中点H,CF的中点Q,连接MH,NQ,过点M作MK⊥NQ于K,
∵EF∥BC,AB∥CD,
∴四边形BCFE是平行四边形,
又∵∠BCD=90°,
∴四边形BCFE是矩形,
∴EF=BC=AD=8,
∵M、N分别为GD、EC的中点,H是DF的中点,Q是CF的中点,
∴NQ=EF=4,MH=GF=1,MH∥EF,NQ∥EF,HQ=CD=3,
∴MH∥NQ,
∵KM⊥NQ,∠NQD=90°,
∴MK∥HQ,
∴四边形MHQK是平行四边形,
∴MK=3,KQ=MH=1,
∴NK=3,
∴MN=MK=3,
方法二,连接BF,连接FM并延长交AD于H,连接BH,
∵EF∥BC,AB∥CD,
∴四边形BCFE是平行四边形,
又∵∠BCD=90°,
∴四边形BCFE是矩形,
∴BN=FN,
∵AD∥EF,
∴∠ADM=∠DGF,∠DHM=∠GFM,
又∵DM=MG,
∴△DHM≌△GFM(AAS),
∴DH=GF=2,HM=FM,
∴BH=2MN,
∵AB=6,AH=AD﹣HD=6,
∴BH=6,
∴NM=3,
故答案为3.
14.解:连接AC,当点D'在AC上时,CD'有最小值,
∵四边形ABCD是矩形,AB=12,AD=5,
∴∠D=∠B=90°,AD=BC,
∴AC=,
由折叠性质得:AD=AD'=5,∠AD'P=∠D=90°,
∴CD'的最小值=AC﹣AD'=13﹣5=8,
故答案为:8.
15.解:∵四边形ABCD是矩形,
∴BD=2OA=2OD,
∵OE:ED=1:3,
∴设OE=x,ED=3x,
则OD=2x,
∵AE⊥BD,AE=,
在Rt△OEA中,根据勾股定理,得
x2+()2=(2x)2,
解得x=1,
∴BD=4.
故答案为:4.
16.解:连接CD,如图所示:
∵∠ACB=90°,AC=3,BC=2,
∴AB===,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
此时,S△ABC=BC AC=AB CD,
即 ×2×3=××CD,
解得:CD=,
∴EF=,
故答案为:.
17.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故答案为:35.
18.解:∵∠BOC=120°,
∴∠AOB=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,AO=OC,BO=DO,
∴AO=BO,
∴△AOB是等边三角形,
∴AB=AO=BO,
∵AB=3,
∴AO=3,
∴AC=2AO=6,
由勾股定理得:BC===3,
故答案为:3.
三.解答题(共8小题,满分58分)
19.解:(1)如图所示:作PH⊥AB于H,
由题意得,DP=4,AQ=2,
则QH=2,又PH=AD=6,
由勾股定理得,PQ===2,
故答案为:2;
(2)当PQ=PB时,
如图,QH=BH,
则t+2t=8,
解得,t=;
(3)当PQ=BQ时,
(2t﹣t)2+62=(8﹣t)2,
解得,t=.
20.证明:∵四边形ABCD是矩形,对角线AC,BD相交于点O,
∴OA=OC=OB=OD,
∵AE⊥BD,DF⊥AC,
∴∠AEO=∠DFO=90°,
在△AOE和△DOF中,
,
∴△AOE≌△DOF(AAS),
∴AE=DF.
21.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,
∴∠BAN=∠AMD,
∵BN⊥AM,
∴∠BNA=90°,
在△ABN和△MAD中,
,
∴△ABN≌△MAD(AAS);
(2)解:∵△ABN≌△MAD,
∴BN=AD,
∵AD=2,
∴BN=2,
又∵AN=4,
在Rt△ABN中,AB===2,
∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,
∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.
22.解:(2):如图一所示:
∵AB=CD,EF=GH,
∴四边形为平行四边形.(两组对边相等的四边形为平行四边形)
(3)如图二所示
由(2)知四边形为平行四边形,
∵∠C为直角,
∴四边形为矩形.(一个角为直角的平行四边形为矩形)
故答案为:(2)平行四边,两组对边分别相等的四边形是平行四边形;
(3)矩,有一个角是直角的平行四边形是矩形.
23.解:∵D是BC的中点,E是BF的中点,
∴DE是△BCF的中位线,
∴DE∥FC,DE=FC,
∵E是AD的中点,
∴DE=AD,
∴AD=FC,
∴四边形ADCF是平行四边形,
又∵D是BC的中点,AB=AC,
∴∠ADC=90°,
∴平行四边形ADCF是矩形.
24.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形;
(2)解:若∠A=40°,当∠BOD=80°时,四边形BECD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=40°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=80°﹣40°=40°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形.
25.解:(1)如图所示:
∵AB=2,BC=3,
∴AC==,
∵△ABE关于AE的轴对称图形为△FAE,
∴AF=AB=2,
∴FC=AC﹣AF=﹣2.
(2)当△FCE是直角三角形时,
①当∠CFE是直角时,如(1)图所示:
由题意可知点F在对角线AC上,且EF⊥AC,
设BE=x,则EF=x,
∴S△ABC=×3×2=3,
S△ABE=×2×x=x,
S△ACE=××x,
∴3=x+x,
解得:x=2﹣4.
∴BE=2﹣4.
②当∠FCE是直角时,如图所示:
∵△ABE关于AE的轴对称图形为△FAE.
∴AB=AF,BE=EF,
在Rt△ADF中,AD=3,AF=2,
∴DF===,
CF=DC﹣CE=2﹣=,
设BE=x,则EF=x,CE=3﹣x,
∴在Rt△ADF中,
EF2=CE2+CF2,
x2=(3﹣x)2+,
解得:x=2,
∴BE=EF=2;
③当E在BC延长线上时,此时∠CEF是直角,如图所示:
由题意得:BE=AB=EF=2.
④当E在BC延长线上,∠ECF=90°时,如图所示:
在Rt△ADF中,
DF====,
∴CF=3,
设BE=t,则EF=t,CE=t﹣3,
在Rt△ECF中,
∵CF2+CE2=EF2,
即(3)2+(t﹣3)2=t2,
解得:t=6,
∴BE=6.
26.(1)证明:∵AB=AC,
∴∠B=∠2,
又∵四边形ABDE是平行四边形,
∴AB∥DE,
∴∠B=∠1,
∴∠1=∠2;
(2)证明:∵四边形ABDE是平行四边形,
∴AB=ED,
∵AB=AC,
∴AC=ED,
在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(3)解:点D在BC的中点上时,四边形ADCE是矩形,理由如下:
∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长BC的中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
