2021—2022学年鲁教版(五四制)八年级数学下册第6章特殊平行四边形同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)八年级数学下册第6章特殊平行四边形同步达标测试题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 538.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 12:11:40 | ||
图片预览

文档简介
2021-2022学年鲁教版八年级数学下册《第6章特殊平行四边形》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
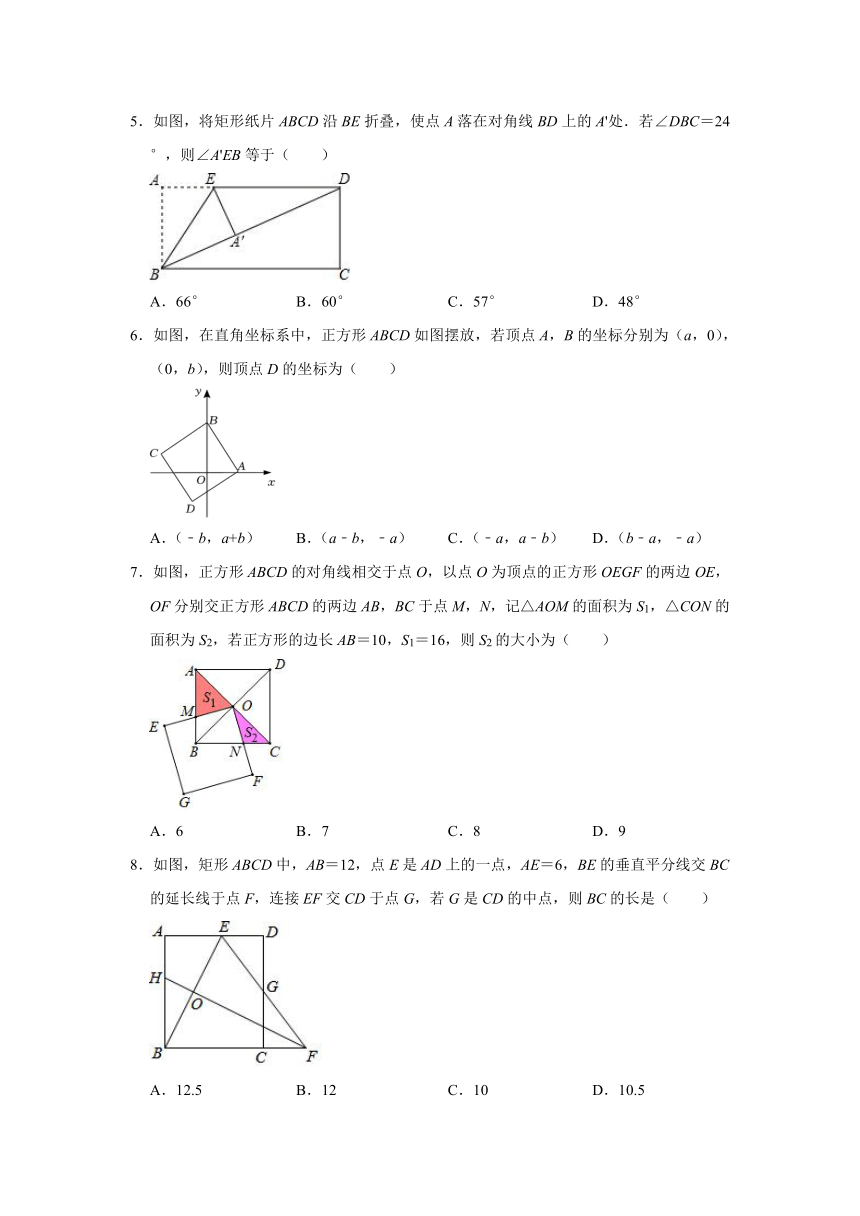
1.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ACDB是菱形的依据是( )
A.对角线互相垂直的平行四边形是菱形 B.对角线平分一组对角的四边形是菱形
C.一组邻边相等的四边形是菱形 D.四条边相等的四边形是菱形
2.如图,在菱形ABCD中,添加一个条件不能证明△ABE≌△CDF的是( )
A.∠BAE=∠FCD B.∠BEA=∠DFC C.AE=CF D.BE=DF
3.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )
A.1 B. C. D.2
4.如图,在矩形ABCD中,点E是AD上任一点,连接CE,F是CE的中点,若△BFC的面积为6,则矩形ABCD的面积为( )
A.18 B.24 C.30 D.36
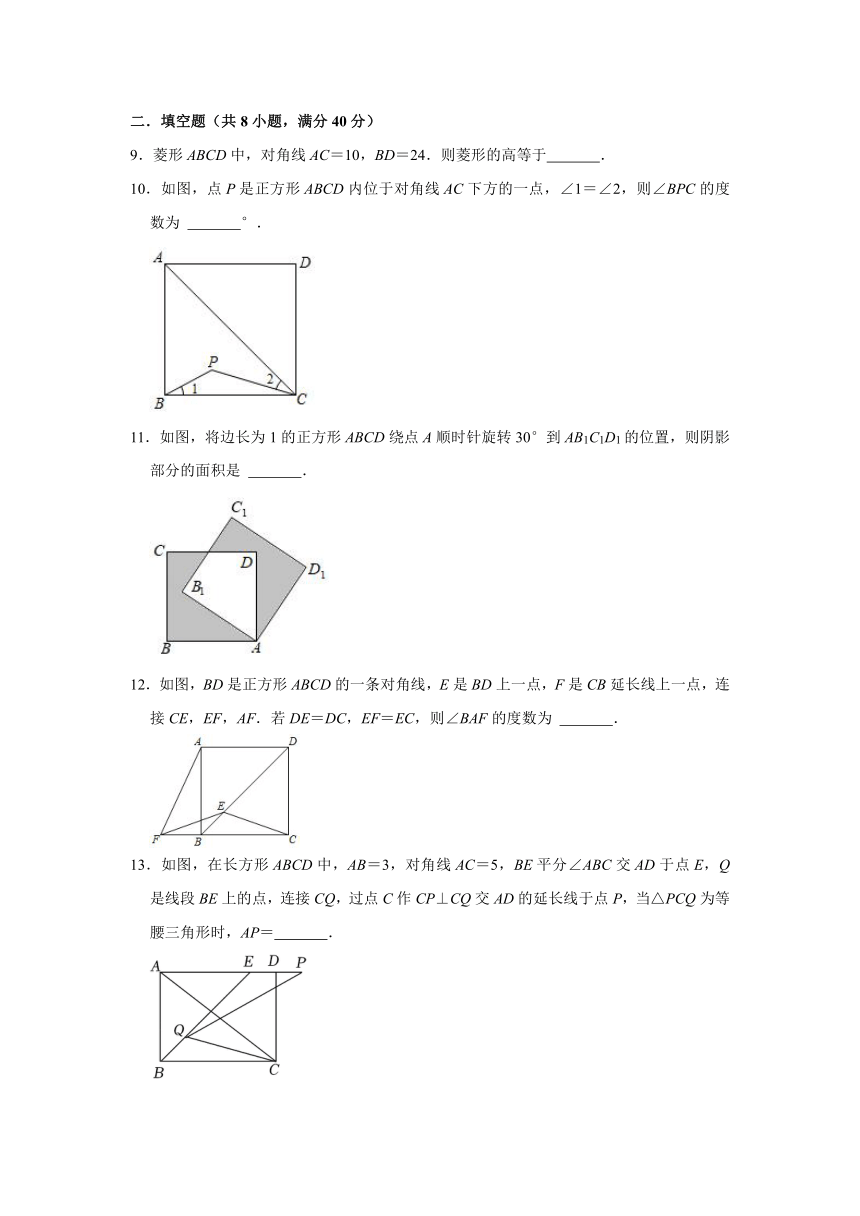
5.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
6.如图,在直角坐标系中,正方形ABCD如图摆放,若顶点A,B的坐标分别为(a,0),(0,b),则顶点D的坐标为( )
A.(﹣b,a+b) B.(a﹣b,﹣a) C.(﹣a,a﹣b) D.(b﹣a,﹣a)
7.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记△AOM的面积为S1,△CON的面积为S2,若正方形的边长AB=10,S1=16,则S2的大小为( )
A.6 B.7 C.8 D.9
8.如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G,若G是CD的中点,则BC的长是( )
A.12.5 B.12 C.10 D.10.5
二.填空题(共8小题,满分40分)
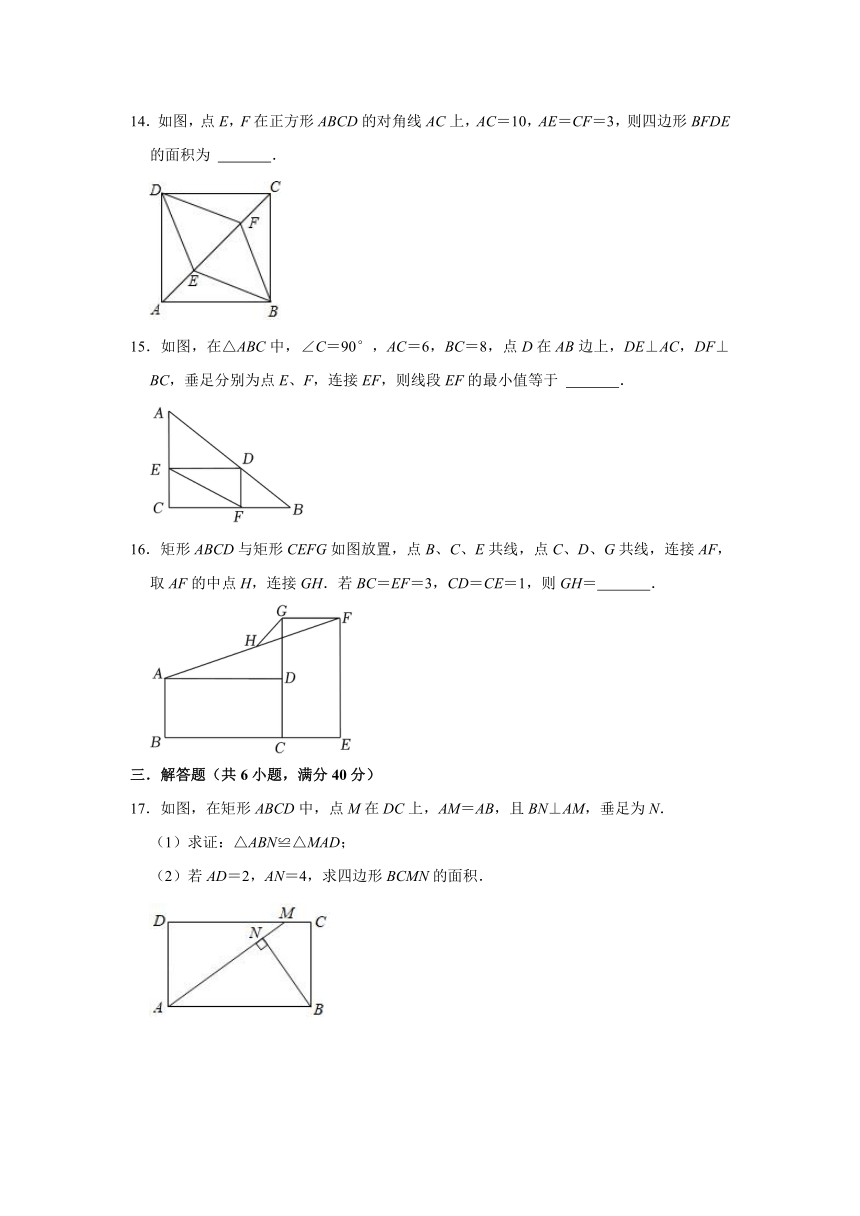
9.菱形ABCD中,对角线AC=10,BD=24.则菱形的高等于 .
10.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
11.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置,则阴影部分的面积是 .
12.如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE,EF,AF.若DE=DC,EF=EC,则∠BAF的度数为 .
13.如图,在长方形ABCD中,AB=3,对角线AC=5,BE平分∠ABC交AD于点E,Q是线段BE上的点,连接CQ,过点C作CP⊥CQ交AD的延长线于点P,当△PCQ为等腰三角形时,AP= .
14.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .
15.如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于 .
16.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH= .
三.解答题(共6小题,满分40分)
17.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD;
(2)若AD=2,AN=4,求四边形BCMN的面积.
18.如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
求证:(1)△ABE≌△DCF;
(2)四边形AEFD是平行四边形.
19.如图,点E是正方形ABCD的边BC上的动点,∠AEF=90°,且EF=AE,FH⊥BH.
(1)求证:BE=CH;
(2)连接DF,若AB=3,BE=x,用含x的代数式表示DF的长.
20.如图,在 ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=2,BF=2,CE=1,求 ABCD的面积.
21.(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF=∠BAD,此时(1)中的结论是否仍然成立?请说明理由.
22.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是 (直接写出结果不写解答过程).
参考答案
一.选择题(共8小题,满分40分)
1.解:由作图得:BA=BD,CA=CD,
∵AB=AC,
∴AB=AC=BD=CD,
∴四边形ACDB是菱形,
故选:D.
2.解:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,∠ABE=∠CDF,
A、添加∠BAE=∠FCD,利用ASA能得出△ABE≌△CDF,不符合题意;
B、添加∠BEA=∠DFC,利用AAS能得出△ABE≌△CDF,不符合题意;
C、添加AE=CF,不能得出△ABE≌△CDF,符合题意;
D、添加BE=DF,利用SAS能得出△ABE≌△CDF,不符合题意;
故选:C.
3.解:∵四边形ABCD是正方形,
∴∠FBC=∠DCE=90°,CD=BC=3,
Rt△DCE中,∠CDE=30°,
∴CE=DE,
设CE=x,则DE=2x,
根据勾股定理得:DC2+CE2=DE2,
即32+x2=(2x)2,
解得:x=±(负值舍去),
∴CE=,
∵DE⊥CF,
∴∠DOC=90°,
∴∠DCO=60°,
∴∠BCF=90°﹣60°=30°=∠CDE,
∵∠DCE=∠CBF,CD=BC,
∴△DCE≌△CBF(ASA),
∴BF=CE=.
故选:C.
4.解:连接BE,如图所示:
∵BF是△BCE的中线,
∴S△BCE=2S△BCF=12,
又∵矩形ABCD与△BCE同底等高,
∴矩形ABCD的面积=2×S△BCE=24.
故选:B.
5.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
6.解:过D作DE⊥x轴于E,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵∠AOB=∠AED=90°,
∴∠BAO+∠DAO=∠ABO+∠BAO=90°,
∴∠ABO=∠DAO,
∴△ABO≌△DAE(AAS),
∴DE=OA,AE=OB,
∵点A,B的坐标分别为(a,0),(0,b),
∴OA=a,OB=b,
∴DE=a,AE=b,
∴OE=b﹣a,
∴顶点D的坐标为(a﹣b,﹣a),
故选:B.
7.解:∵四边形ABCD和四边形OA'B'C'都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠A'OC'=90°,
∴∠A'OB=∠COC'.
在△OBM与△OCN中,
,
∴△OBM≌△OCN(ASA),
∴S1+S2=S△OAB=×10×10=25,
∴S2=25﹣16=9,
故选:D.
8.解:∵矩形ABCD中,G是CD的中点,AB=12,
∴CG=DG=×12=6,
在△DEG和△CFG中,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
设DE=x,
则BF=BC+CF=AD+CF=6+x+x=6+2x,
在Rt△DEG中,EG==,
∴EF=2,
∵FH垂直平分BE,
∴BF=EF,
∴6+2x=2,
解得x=4.5,
∴AD=AE+DE=6+4.5=10.5,
∴BC=AD=10.5.
故选:D.
二.填空题(共8小题,满分40分)
9.解:由题意得,菱形的面积=×AC BD=×10×24=120,
则AO=5,BO=12,
则AB==13,
设菱形的高为h,
则菱形的面积=BC h=13h=120,
解得h=,
故答案为.
10.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
11.解:如图,
连接AE,根据题意可知AB1=AD=1,∠B1=∠D=90°,∠BAB1=30°,
在Rt△AB1E和Rt△ADE中,
,
∴Rt△AB1E≌Rt△ADE(HL),
∵∠B1AE=∠DAE=∠B1AD=30°,
∴=,解得DE=,
∴S四边形ADEB1=2S△ADE=2××AD×DE=,
∴S阴影部分=2(S正方形ABCD﹣S四边形ADEB1)=2×(1﹣)=2﹣,
故答案为:2﹣.
12.解:如右图,连接AE,
∵BD为正方形ABCD的对角线,
∴∠BDC=45°,
∵DE=DC=AD,
∴∠DEC=∠DCE==67.5°,
∵∠DCB=90°,
∴∠BCE=90°﹣∠DCE=90°﹣67.5°=22.5°,
∵EF=EC,
∴∠FEC=180°﹣∠EFC﹣∠ECF=180°﹣22.5°﹣22.5°=135°,
∵∠BEC=180°﹣∠DEC=180°﹣67.5°=112.5°,
∴∠BEF=135°﹣112.5°=22.5°,
∵AD=DE,∠ADE=45°,
∴∠AED==67.5°,
∴∠BEF+∠AED=22.5°+67.5°=90°,
∴∠AEF=180°﹣90°=90°,
在△ADE和△EDC中,
,
∴△ADE≌△EDC(SAS),
∴AE=EC,
∴AE=EF,
即△AEF为等腰直角三角形,
∴∠AFE=45°,
∴∠AFB=∠AFE+∠BFE=45°+22.5°=67.5°,
∵∠ABF=90°,
∴∠BAF=90°﹣∠AFB=90°﹣67.5°=22.5°,
故答案为:22.5°.
13.解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠ADC=90°,AD=BC,CD=AB=3,
∵∠BCD=∠QCP=90°,
∴∠QCH=∠PCD,
∵AB=3,AC=5,
∴BC==4,
∴AD=BC=4,
过Q作QH⊥BC于H,
∴∠QHB=∠QHC=90°,
∵BE平分∠ABC交AD于点E,
∴∠QBH=45°,
∴△BQH是等腰直角三角形,
∴BH=QH,
∵CP⊥CQ,
∴∠QCP=90°,
∵△PCQ为等腰三角形,
∴CQ=CP,
∵∠CDP=∠CHQ=90°,∠QCH=∠PCD,
∴△CQH≌△CPD(AAS),
∴CH=CD=3,
∴BH=QH=1,
∴PD=QH=1,
∴AP=AD+PD=5,
故答案为:5.
14.解:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形,
∴BD=AC=10,
∵AE=CF=3,
∴EF=4,
∴四边形BFDE的面积为BD EF=×10×4=20.
故答案为:20.
15.解:如图,连接CD.
∵∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
∵S△ABC=BC AC=AB CD,
∴×8×6=×10×CD,
解得CD=4.8,
∴EF=4.8.
故答案为:4.8.
16.解:延长GH交AD于M点,如图所示:
∵四边形ABCD与四边形CEFG都是矩形,
∴CD=CE=FG=1,BC=EF=CG=3,BE∥AD∥FG,
∴DG=CG﹣CD=3﹣1=2,∠HAM=∠HFG,
∵AF的中点H,
∴AH=FH,
在△AMH和△FGH中,
,
∴△AMH≌△FGH(ASA).
∴AM=FG=1,MH=GH,
∴MD=AD﹣AM=3﹣1=2,
在Rt△MDG中,GM===2,
∴GH=GM=,
故答案为:.
三.解答题(共6小题,满分40分)
17.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,
∴∠BAN=∠AMD,
∵BN⊥AM,
∴∠BNA=90°,
在△ABN和△MAD中,
,
∴△ABN≌△MAD(AAS);
(2)解:∵△ABN≌△MAD,
∴BN=AD,
∵AD=2,
∴BN=2,
又∵AN=4,
在Rt△ABN中,AB===2,
∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,
∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.
18.证明:(1)∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°,AD=BC,AD∥BC,
∴∠ABE=∠DCF=90°,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
(2)∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF=AD,
又∵AD∥BC,
∴四边形AEFD是平行四边形.
19.(1)证明:∵正方形ABCD,
∴∠B=90°,AB=BC,
∵FH⊥BH,
∴∠H=90°=∠B,∠EFH=90°﹣∠FEH,
∵∠AEF=90°,
∴∠AEB=90°﹣∠FEH,
∴∠AEB=∠F,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(AAS),
∴EH=AB=BC,BE=FH,
∴EH﹣EC=BC﹣EC,即CH=BE;
(2)过F作FP⊥CD于P,如图,
∵∠H=∠DCH=∠FPC=90°,
∴四边形PCHF是矩形,
由(1)知:BE=FH=CH,
∴四边形PCHF是正方形,
∴PF=CP=CH=BE=x,
∵DC=AB=3,
∴DP=DC﹣CP=3﹣x,
Rt△DPF中,DF=,
∴DF==.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)解:作FG⊥BC于G,
∵四边形ABEF是菱形,若AE=2,BF=2,
∴AE⊥BF,OE=AE=1,OB=BF=,
∴BE==2,
∵S菱形ABEF= AE BF=BE FG,
∴GF=,
∴S平行四边形ABCD=BC FG=(BE+EC) GF=(2+1)×=3.
21.解:(1)如图1,
EF=BE+DF,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABM=90°,
又∵BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵∠EAF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=∠MAE=45°=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF,
(2)如图2,
EF=BE+DF,仍然成立,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠4=180°,
∴∠D=∠4,
又∵AB=AD,BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵,
∴∠1+∠3=∠EAF,
∴∠MAE=∠2+∠3=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF.
22.解:(1)∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFE=DFE,∠AEF=BEF,
∴∠AEF+∠AFE=(∠DFE+∠BEF)=270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=3,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2;
(3)解:如图2所示:
把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,
由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=5,
∴GQ=3,
设MR=HR=a,则GR=5﹣a,QR=a+2,
在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,
解得:a=,即HR=;
故答案为:.
一.选择题(共8小题,满分40分)
1.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ACDB是菱形的依据是( )
A.对角线互相垂直的平行四边形是菱形 B.对角线平分一组对角的四边形是菱形
C.一组邻边相等的四边形是菱形 D.四条边相等的四边形是菱形
2.如图,在菱形ABCD中,添加一个条件不能证明△ABE≌△CDF的是( )
A.∠BAE=∠FCD B.∠BEA=∠DFC C.AE=CF D.BE=DF
3.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )
A.1 B. C. D.2
4.如图,在矩形ABCD中,点E是AD上任一点,连接CE,F是CE的中点,若△BFC的面积为6,则矩形ABCD的面积为( )
A.18 B.24 C.30 D.36
5.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
6.如图,在直角坐标系中,正方形ABCD如图摆放,若顶点A,B的坐标分别为(a,0),(0,b),则顶点D的坐标为( )
A.(﹣b,a+b) B.(a﹣b,﹣a) C.(﹣a,a﹣b) D.(b﹣a,﹣a)
7.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记△AOM的面积为S1,△CON的面积为S2,若正方形的边长AB=10,S1=16,则S2的大小为( )
A.6 B.7 C.8 D.9
8.如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G,若G是CD的中点,则BC的长是( )
A.12.5 B.12 C.10 D.10.5
二.填空题(共8小题,满分40分)
9.菱形ABCD中,对角线AC=10,BD=24.则菱形的高等于 .
10.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
11.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置,则阴影部分的面积是 .
12.如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE,EF,AF.若DE=DC,EF=EC,则∠BAF的度数为 .
13.如图,在长方形ABCD中,AB=3,对角线AC=5,BE平分∠ABC交AD于点E,Q是线段BE上的点,连接CQ,过点C作CP⊥CQ交AD的延长线于点P,当△PCQ为等腰三角形时,AP= .
14.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .
15.如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于 .
16.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH= .
三.解答题(共6小题,满分40分)
17.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD;
(2)若AD=2,AN=4,求四边形BCMN的面积.
18.如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
求证:(1)△ABE≌△DCF;
(2)四边形AEFD是平行四边形.
19.如图,点E是正方形ABCD的边BC上的动点,∠AEF=90°,且EF=AE,FH⊥BH.
(1)求证:BE=CH;
(2)连接DF,若AB=3,BE=x,用含x的代数式表示DF的长.
20.如图,在 ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=2,BF=2,CE=1,求 ABCD的面积.
21.(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF=∠BAD,此时(1)中的结论是否仍然成立?请说明理由.
22.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是 (直接写出结果不写解答过程).
参考答案
一.选择题(共8小题,满分40分)
1.解:由作图得:BA=BD,CA=CD,
∵AB=AC,
∴AB=AC=BD=CD,
∴四边形ACDB是菱形,
故选:D.
2.解:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,∠ABE=∠CDF,
A、添加∠BAE=∠FCD,利用ASA能得出△ABE≌△CDF,不符合题意;
B、添加∠BEA=∠DFC,利用AAS能得出△ABE≌△CDF,不符合题意;
C、添加AE=CF,不能得出△ABE≌△CDF,符合题意;
D、添加BE=DF,利用SAS能得出△ABE≌△CDF,不符合题意;
故选:C.
3.解:∵四边形ABCD是正方形,
∴∠FBC=∠DCE=90°,CD=BC=3,
Rt△DCE中,∠CDE=30°,
∴CE=DE,
设CE=x,则DE=2x,
根据勾股定理得:DC2+CE2=DE2,
即32+x2=(2x)2,
解得:x=±(负值舍去),
∴CE=,
∵DE⊥CF,
∴∠DOC=90°,
∴∠DCO=60°,
∴∠BCF=90°﹣60°=30°=∠CDE,
∵∠DCE=∠CBF,CD=BC,
∴△DCE≌△CBF(ASA),
∴BF=CE=.
故选:C.
4.解:连接BE,如图所示:
∵BF是△BCE的中线,
∴S△BCE=2S△BCF=12,
又∵矩形ABCD与△BCE同底等高,
∴矩形ABCD的面积=2×S△BCE=24.
故选:B.
5.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
6.解:过D作DE⊥x轴于E,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵∠AOB=∠AED=90°,
∴∠BAO+∠DAO=∠ABO+∠BAO=90°,
∴∠ABO=∠DAO,
∴△ABO≌△DAE(AAS),
∴DE=OA,AE=OB,
∵点A,B的坐标分别为(a,0),(0,b),
∴OA=a,OB=b,
∴DE=a,AE=b,
∴OE=b﹣a,
∴顶点D的坐标为(a﹣b,﹣a),
故选:B.
7.解:∵四边形ABCD和四边形OA'B'C'都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠A'OC'=90°,
∴∠A'OB=∠COC'.
在△OBM与△OCN中,
,
∴△OBM≌△OCN(ASA),
∴S1+S2=S△OAB=×10×10=25,
∴S2=25﹣16=9,
故选:D.
8.解:∵矩形ABCD中,G是CD的中点,AB=12,
∴CG=DG=×12=6,
在△DEG和△CFG中,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
设DE=x,
则BF=BC+CF=AD+CF=6+x+x=6+2x,
在Rt△DEG中,EG==,
∴EF=2,
∵FH垂直平分BE,
∴BF=EF,
∴6+2x=2,
解得x=4.5,
∴AD=AE+DE=6+4.5=10.5,
∴BC=AD=10.5.
故选:D.
二.填空题(共8小题,满分40分)
9.解:由题意得,菱形的面积=×AC BD=×10×24=120,
则AO=5,BO=12,
则AB==13,
设菱形的高为h,
则菱形的面积=BC h=13h=120,
解得h=,
故答案为.
10.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
11.解:如图,
连接AE,根据题意可知AB1=AD=1,∠B1=∠D=90°,∠BAB1=30°,
在Rt△AB1E和Rt△ADE中,
,
∴Rt△AB1E≌Rt△ADE(HL),
∵∠B1AE=∠DAE=∠B1AD=30°,
∴=,解得DE=,
∴S四边形ADEB1=2S△ADE=2××AD×DE=,
∴S阴影部分=2(S正方形ABCD﹣S四边形ADEB1)=2×(1﹣)=2﹣,
故答案为:2﹣.
12.解:如右图,连接AE,
∵BD为正方形ABCD的对角线,
∴∠BDC=45°,
∵DE=DC=AD,
∴∠DEC=∠DCE==67.5°,
∵∠DCB=90°,
∴∠BCE=90°﹣∠DCE=90°﹣67.5°=22.5°,
∵EF=EC,
∴∠FEC=180°﹣∠EFC﹣∠ECF=180°﹣22.5°﹣22.5°=135°,
∵∠BEC=180°﹣∠DEC=180°﹣67.5°=112.5°,
∴∠BEF=135°﹣112.5°=22.5°,
∵AD=DE,∠ADE=45°,
∴∠AED==67.5°,
∴∠BEF+∠AED=22.5°+67.5°=90°,
∴∠AEF=180°﹣90°=90°,
在△ADE和△EDC中,
,
∴△ADE≌△EDC(SAS),
∴AE=EC,
∴AE=EF,
即△AEF为等腰直角三角形,
∴∠AFE=45°,
∴∠AFB=∠AFE+∠BFE=45°+22.5°=67.5°,
∵∠ABF=90°,
∴∠BAF=90°﹣∠AFB=90°﹣67.5°=22.5°,
故答案为:22.5°.
13.解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠ADC=90°,AD=BC,CD=AB=3,
∵∠BCD=∠QCP=90°,
∴∠QCH=∠PCD,
∵AB=3,AC=5,
∴BC==4,
∴AD=BC=4,
过Q作QH⊥BC于H,
∴∠QHB=∠QHC=90°,
∵BE平分∠ABC交AD于点E,
∴∠QBH=45°,
∴△BQH是等腰直角三角形,
∴BH=QH,
∵CP⊥CQ,
∴∠QCP=90°,
∵△PCQ为等腰三角形,
∴CQ=CP,
∵∠CDP=∠CHQ=90°,∠QCH=∠PCD,
∴△CQH≌△CPD(AAS),
∴CH=CD=3,
∴BH=QH=1,
∴PD=QH=1,
∴AP=AD+PD=5,
故答案为:5.
14.解:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形,
∴BD=AC=10,
∵AE=CF=3,
∴EF=4,
∴四边形BFDE的面积为BD EF=×10×4=20.
故答案为:20.
15.解:如图,连接CD.
∵∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
∵S△ABC=BC AC=AB CD,
∴×8×6=×10×CD,
解得CD=4.8,
∴EF=4.8.
故答案为:4.8.
16.解:延长GH交AD于M点,如图所示:
∵四边形ABCD与四边形CEFG都是矩形,
∴CD=CE=FG=1,BC=EF=CG=3,BE∥AD∥FG,
∴DG=CG﹣CD=3﹣1=2,∠HAM=∠HFG,
∵AF的中点H,
∴AH=FH,
在△AMH和△FGH中,
,
∴△AMH≌△FGH(ASA).
∴AM=FG=1,MH=GH,
∴MD=AD﹣AM=3﹣1=2,
在Rt△MDG中,GM===2,
∴GH=GM=,
故答案为:.
三.解答题(共6小题,满分40分)
17.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,
∴∠BAN=∠AMD,
∵BN⊥AM,
∴∠BNA=90°,
在△ABN和△MAD中,
,
∴△ABN≌△MAD(AAS);
(2)解:∵△ABN≌△MAD,
∴BN=AD,
∵AD=2,
∴BN=2,
又∵AN=4,
在Rt△ABN中,AB===2,
∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,
∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.
18.证明:(1)∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°,AD=BC,AD∥BC,
∴∠ABE=∠DCF=90°,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
(2)∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF=AD,
又∵AD∥BC,
∴四边形AEFD是平行四边形.
19.(1)证明:∵正方形ABCD,
∴∠B=90°,AB=BC,
∵FH⊥BH,
∴∠H=90°=∠B,∠EFH=90°﹣∠FEH,
∵∠AEF=90°,
∴∠AEB=90°﹣∠FEH,
∴∠AEB=∠F,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(AAS),
∴EH=AB=BC,BE=FH,
∴EH﹣EC=BC﹣EC,即CH=BE;
(2)过F作FP⊥CD于P,如图,
∵∠H=∠DCH=∠FPC=90°,
∴四边形PCHF是矩形,
由(1)知:BE=FH=CH,
∴四边形PCHF是正方形,
∴PF=CP=CH=BE=x,
∵DC=AB=3,
∴DP=DC﹣CP=3﹣x,
Rt△DPF中,DF=,
∴DF==.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)解:作FG⊥BC于G,
∵四边形ABEF是菱形,若AE=2,BF=2,
∴AE⊥BF,OE=AE=1,OB=BF=,
∴BE==2,
∵S菱形ABEF= AE BF=BE FG,
∴GF=,
∴S平行四边形ABCD=BC FG=(BE+EC) GF=(2+1)×=3.
21.解:(1)如图1,
EF=BE+DF,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABM=90°,
又∵BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵∠EAF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=∠MAE=45°=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF,
(2)如图2,
EF=BE+DF,仍然成立,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠4=180°,
∴∠D=∠4,
又∵AB=AD,BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵,
∴∠1+∠3=∠EAF,
∴∠MAE=∠2+∠3=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF.
22.解:(1)∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFE=DFE,∠AEF=BEF,
∴∠AEF+∠AFE=(∠DFE+∠BEF)=270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=3,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2;
(3)解:如图2所示:
把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,
由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=5,
∴GQ=3,
设MR=HR=a,则GR=5﹣a,QR=a+2,
在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,
解得:a=,即HR=;
故答案为:.
