北京版九年级下册 体会代数综合问题的形成过程 教案
文档属性
| 名称 | 北京版九年级下册 体会代数综合问题的形成过程 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 227.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 00:00:00 | ||
图片预览

文档简介
体会代数综合问题的形成过程
教学目标:
知识技能:
1.会求带字母的二次函数的对称轴,顶点坐标,与y轴的交点;
2.在只给带有字母系数的二次函数的解析式的情况下,有哪些思考方向 。
(二)数学思考:
在只给带有字母系数的二次函数的解析式的情况下,能做什么?
如果想进一步形成数学问题,该如何添加条件?
二次函数与坐标轴、直线、双曲线都有哪些联系?
(三)问题解决:
1. .巩固二次函数的对称轴、顶点、与坐标轴的交点的求解方法.
2.通过解析一些代数综合问题,体会综合问题的形成过程;
3.在解决综合问题时,体会知识之间的内在联系.
(四)情感态度价值观:
鼓励尝试自己设计代数综合问题,激发学生尝试补充条件建立综合问题的兴趣,增强解决代数综合问题的信心和勇于探索知识之间内在联系的思维品质。
教学重点
体会代数综合问题的形成过程解决,感知知识之间的内在联系.
三、教学难点
在给了带有字母系数的二次函数的解析式的情况下,再添加什么条件可以进一步形成数学问题是很开放和有思维深度的,也是学生课下研究的一个方向.
四、教学过程
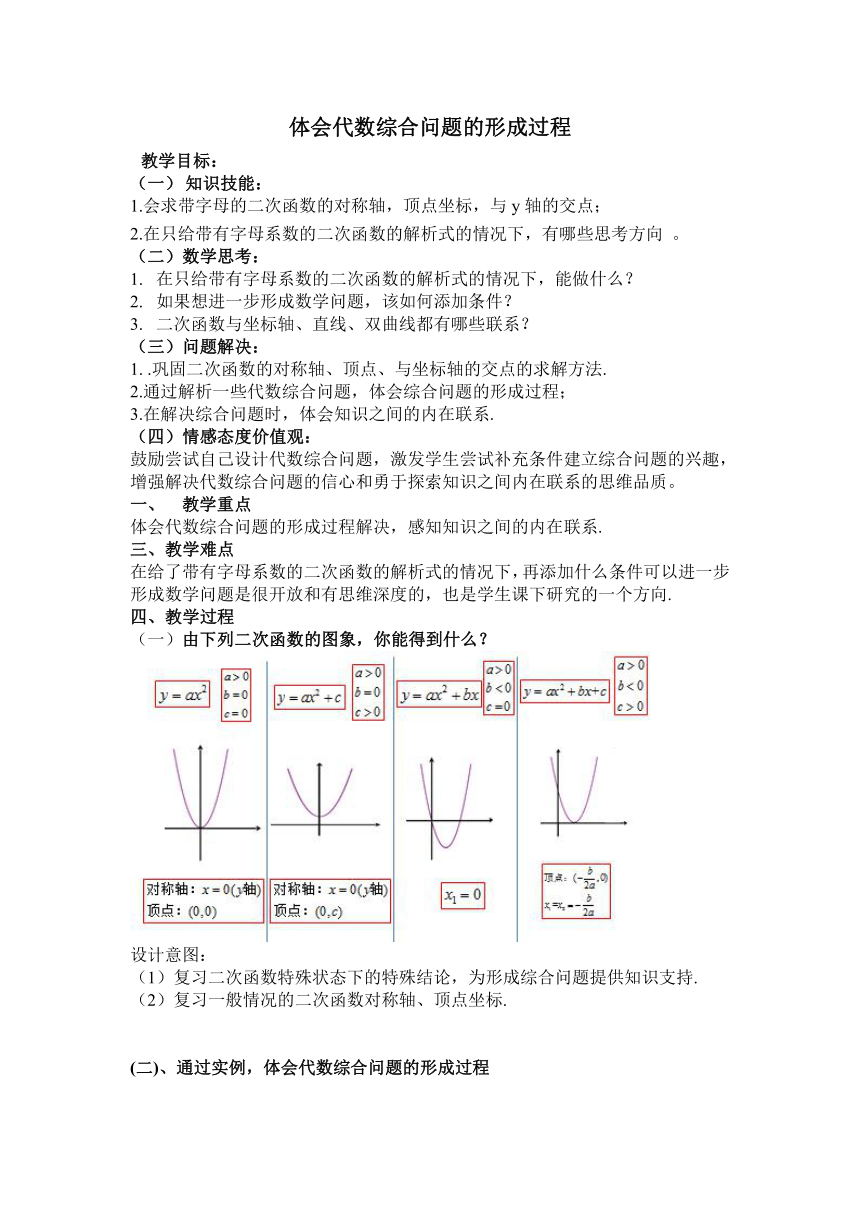
(一)由下列二次函数的图象,你能得到什么?
设计意图:
(1)复习二次函数特殊状态下的特殊结论,为形成综合问题提供知识支持.
(2)复习一般情况的二次函数对称轴、顶点坐标.
(二)、通过实例,体会代数综合问题的形成过程
问题:
教师活动 学生活动
教师提问: (1) 解析式告诉我们什么? 预设学生思考回答: (1)能得到抛物线与y轴的交点(0, 2) (2)能得到抛物线的对称轴:直线 ; (3)可以表示抛物线的顶点坐标:
教师活动 学生活动
教师提问: (1) 你可以尝试再添加什么条件,从而形成数学问题? 学生活动尝试给出条件形成问题
有了这样或那样的思考,我们看看2013年北京中考27题是如何进一步设计数学问题的?
它先做了一个铺垫,找到直线AB的对称直线l,结合抛物线的对称性给出第三问:
教师分析引导学生思考,体会问题形成的过程:
我们首先发现直线AB与直线l和抛物线一样都关于直线x=2对称,我们画出直线l,看看再介入条件“若该抛物线在 这一段位于直线l的上方”我们应该思考什么呢?结合对称性我们发现:“若该抛物线在 这一段位于直线l的上方,那么该抛物线在 这一段也位于直线l的上方”,那么介入下一个条件“并且在 这一段位于直线AB的下方”就更加明确,实际上“若该抛物线在 这一段位于直线AB的下方,那么该抛物线在 这一段也位于直线AB的下方”,那么抛物线明显必过点(-1,4)或点(3,4),
因此将点(-1,4)代入抛物线的解析式,从而求得。
通过刚才我们逐步的介入条件,我们体会了编制这样综合问题的老师是如何依据题目自身的条件,合理有序的介入条件,形成数学的综合问题的.
问题:
教师活动 学生活动
教师提问: (1) 解析式告诉我们什么? 预设学生思考回答: (1)能得到抛物线与y轴的交点(0, m-1) (2)能得到抛物线的对称轴:直线 ; (3)可以表示抛物线的顶点坐标:
教师活动 学生活动
教师提问: (1) 你可以尝试再添加什么条件,从而形成数学问题? 学生活动尝试给出条件形成问题
有了这样或那样的思考,我们看看2016年北京中考27题是如何进一步设计数学问题的?
教师分析引导学生思考,体会问题形成的过程:
本题也是先做了一个铺垫,给出“整点”的概念,在m=1条件下求线段AB上的整点个数; 紧接着限制了一个由特殊点形成的区域,再限制整点的个数,求m的取值范围?我们会发现抛物线的对称轴始终是直线 ,且顶点 始终不变,当m>0时,越大开口m越小,当整点个数为6个时,抛物线必过点(-1,0)或点(3,0), 当整点个数为8个时,抛物线必过点(-2,0)或点(4,0),选择将(-1,0)代入抛物线的 ,选择将(-2,0)代入抛物线的 ,所以, .
小结:通过刚才我们逐步的介入条件,我们体会了编制这样综合问题的老师是如何依据题目自身的条件,合理有序的介入条件,形成数学的综合问题的.同学们也可以不断地这样去解决这样的综合问题,走到出题人的背后,看看出题人是如何不断的介入条件形成问题的,也可以自己尝试变换条件,看看能形成什么样的综合问题,这样会对同学们解决问题的能力有很好的提升.
教学目标:
知识技能:
1.会求带字母的二次函数的对称轴,顶点坐标,与y轴的交点;
2.在只给带有字母系数的二次函数的解析式的情况下,有哪些思考方向 。
(二)数学思考:
在只给带有字母系数的二次函数的解析式的情况下,能做什么?
如果想进一步形成数学问题,该如何添加条件?
二次函数与坐标轴、直线、双曲线都有哪些联系?
(三)问题解决:
1. .巩固二次函数的对称轴、顶点、与坐标轴的交点的求解方法.
2.通过解析一些代数综合问题,体会综合问题的形成过程;
3.在解决综合问题时,体会知识之间的内在联系.
(四)情感态度价值观:
鼓励尝试自己设计代数综合问题,激发学生尝试补充条件建立综合问题的兴趣,增强解决代数综合问题的信心和勇于探索知识之间内在联系的思维品质。
教学重点
体会代数综合问题的形成过程解决,感知知识之间的内在联系.
三、教学难点
在给了带有字母系数的二次函数的解析式的情况下,再添加什么条件可以进一步形成数学问题是很开放和有思维深度的,也是学生课下研究的一个方向.
四、教学过程
(一)由下列二次函数的图象,你能得到什么?
设计意图:
(1)复习二次函数特殊状态下的特殊结论,为形成综合问题提供知识支持.
(2)复习一般情况的二次函数对称轴、顶点坐标.
(二)、通过实例,体会代数综合问题的形成过程
问题:
教师活动 学生活动
教师提问: (1) 解析式告诉我们什么? 预设学生思考回答: (1)能得到抛物线与y轴的交点(0, 2) (2)能得到抛物线的对称轴:直线 ; (3)可以表示抛物线的顶点坐标:
教师活动 学生活动
教师提问: (1) 你可以尝试再添加什么条件,从而形成数学问题? 学生活动尝试给出条件形成问题
有了这样或那样的思考,我们看看2013年北京中考27题是如何进一步设计数学问题的?
它先做了一个铺垫,找到直线AB的对称直线l,结合抛物线的对称性给出第三问:
教师分析引导学生思考,体会问题形成的过程:
我们首先发现直线AB与直线l和抛物线一样都关于直线x=2对称,我们画出直线l,看看再介入条件“若该抛物线在 这一段位于直线l的上方”我们应该思考什么呢?结合对称性我们发现:“若该抛物线在 这一段位于直线l的上方,那么该抛物线在 这一段也位于直线l的上方”,那么介入下一个条件“并且在 这一段位于直线AB的下方”就更加明确,实际上“若该抛物线在 这一段位于直线AB的下方,那么该抛物线在 这一段也位于直线AB的下方”,那么抛物线明显必过点(-1,4)或点(3,4),
因此将点(-1,4)代入抛物线的解析式,从而求得。
通过刚才我们逐步的介入条件,我们体会了编制这样综合问题的老师是如何依据题目自身的条件,合理有序的介入条件,形成数学的综合问题的.
问题:
教师活动 学生活动
教师提问: (1) 解析式告诉我们什么? 预设学生思考回答: (1)能得到抛物线与y轴的交点(0, m-1) (2)能得到抛物线的对称轴:直线 ; (3)可以表示抛物线的顶点坐标:
教师活动 学生活动
教师提问: (1) 你可以尝试再添加什么条件,从而形成数学问题? 学生活动尝试给出条件形成问题
有了这样或那样的思考,我们看看2016年北京中考27题是如何进一步设计数学问题的?
教师分析引导学生思考,体会问题形成的过程:
本题也是先做了一个铺垫,给出“整点”的概念,在m=1条件下求线段AB上的整点个数; 紧接着限制了一个由特殊点形成的区域,再限制整点的个数,求m的取值范围?我们会发现抛物线的对称轴始终是直线 ,且顶点 始终不变,当m>0时,越大开口m越小,当整点个数为6个时,抛物线必过点(-1,0)或点(3,0), 当整点个数为8个时,抛物线必过点(-2,0)或点(4,0),选择将(-1,0)代入抛物线的 ,选择将(-2,0)代入抛物线的 ,所以, .
小结:通过刚才我们逐步的介入条件,我们体会了编制这样综合问题的老师是如何依据题目自身的条件,合理有序的介入条件,形成数学的综合问题的.同学们也可以不断地这样去解决这样的综合问题,走到出题人的背后,看看出题人是如何不断的介入条件形成问题的,也可以自己尝试变换条件,看看能形成什么样的综合问题,这样会对同学们解决问题的能力有很好的提升.
