§1.2.1 独立性检验的基本思想及其初步应用一
文档属性
| 名称 | §1.2.1 独立性检验的基本思想及其初步应用一 |

|
|
| 格式 | zip | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-19 18:47:06 | ||
图片预览

文档简介
§1.2.1 独立性检验的基本思想及其初步应用一
【学习目标】
1.通过探究“吸烟是否与患肺癌有关系”引出独立性检验的问题,并借助样本数据的列联表、柱形图和条形图展示在吸烟者中患肺癌的比例比不吸烟者中患肺癌的比例高,让学生亲身体验独立性检验的必要性;
2.会根据列联表求统计量.
预 习 案
【自学引导】
一、课前准备
(预习教材P12~ P14,找出疑惑之处)
复习1:回归分析的方法、步骤,刻画模型拟合效果的方法(相关指数、残差分析)、步骤.
二、新课导学
※ 学习探究
新知1:
1.分类变量: .
2. 列联表:
.
试试:你能列举出几个分类变量吗?
探究任务:吸烟与患肺癌的关系
1.由列联表可粗略的看出:
(1)不吸烟者有 患肺癌;
(2)不吸烟者有 患肺癌.
因此,直观上课的结论: .
2.用三维柱柱图和二维条形图直观反映:
(1)根据列联表的数据,作出三维柱形图:
由上图可以直观地看出, 吸烟与患肺癌 .
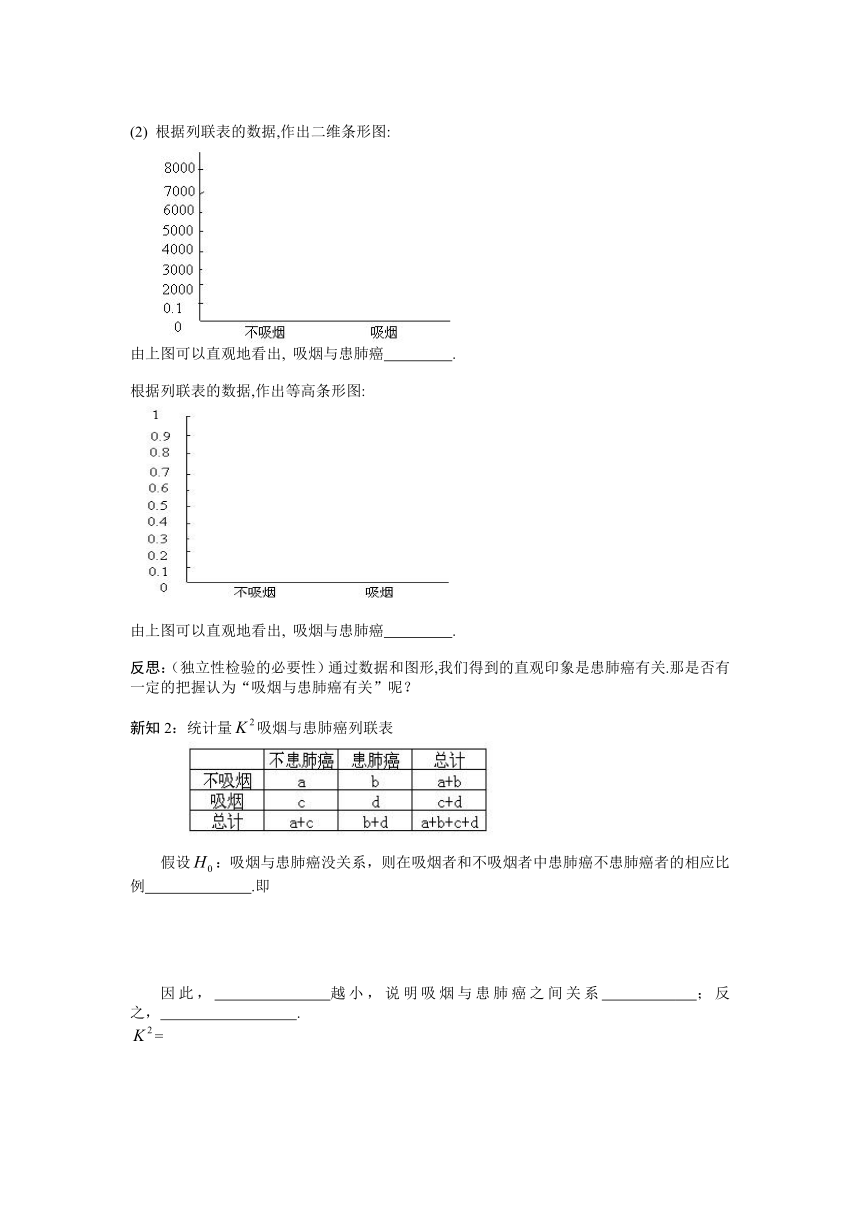
(2) 根据列联表的数据,作出二维条形图:
由上图可以直观地看出, 吸烟与患肺癌 .
根据列联表的数据,作出等高条形图:
由上图可以直观地看出, 吸烟与患肺癌 .
反思:(独立性检验的必要性)通过数据和图形,我们得到的直观印象是患肺癌有关.那是否有一定的把握认为“吸烟与患肺癌有关”呢?
新知2:统计量吸烟与患肺癌列联表
假设:吸烟与患肺癌没关系,则在吸烟者和不吸烟者中患肺癌不患肺癌者的相应比例 .即
因此, 越小,说明吸烟与患肺癌之间关系 ;反之, .
=
探 究 案
※ 典型例题
例1 吸烟与患肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸 烟
2099
49
2148
总 计
9874
91
9965
不健康
健 康
总计
不优秀
41
626
667
优 秀
37
296
333
总 计
78
922
1000
求.
※ 动手试试
练1. 性别与喜欢数学课程列联表:
喜欢数学
不喜欢数学
总 计
男
37
85
122
女
35
143
178
总 计
72
228
300
求.
练习案
※ 当堂检测(时量:5分钟 满分:10分)计分:
1. 分类变量: .
2. 列联表: .
3. 统计量: .
※ 知识拓展
1. 分类变量的取值一定是离散的,而且不同的取值仅表示个体所属的类别,如性别变量,只取男、女两个值,商品的等级变量只取一级、二级、三级,等等. 分类变量的取值有时可用数字来表示,但这时的数字除了分类以外没有其他的含义. 如用“0”表示“男”,用“1”表示“女”.
2. 独立性检验的步骤(略)及原理(与反证法类似):
反证法
假设检验
要证明结论A
备择假设H
在A不成立的前提下进行推理
在H不成立的条件下,即H成立的条件下进行推理
推出矛盾,意味着结论A成立
推出有利于H成立的小概率事件(概率不超过的事件)发生,意味着H成立的可能性(可能性为(1-))很大
没有找到矛盾,不能对A下任何结论,即反证法不成功
推出有利于H成立的小概率事件不发生,接受原假设
课后作业
某市为调查全市高中生学习状况是否对生理健康有影响,随机进行调查并得到如下的列联表:
求.
【学习目标】
1.通过探究“吸烟是否与患肺癌有关系”引出独立性检验的问题,并借助样本数据的列联表、柱形图和条形图展示在吸烟者中患肺癌的比例比不吸烟者中患肺癌的比例高,让学生亲身体验独立性检验的必要性;
2.会根据列联表求统计量.
预 习 案
【自学引导】
一、课前准备
(预习教材P12~ P14,找出疑惑之处)
复习1:回归分析的方法、步骤,刻画模型拟合效果的方法(相关指数、残差分析)、步骤.
二、新课导学
※ 学习探究
新知1:
1.分类变量: .
2. 列联表:
.
试试:你能列举出几个分类变量吗?
探究任务:吸烟与患肺癌的关系
1.由列联表可粗略的看出:
(1)不吸烟者有 患肺癌;
(2)不吸烟者有 患肺癌.
因此,直观上课的结论: .
2.用三维柱柱图和二维条形图直观反映:
(1)根据列联表的数据,作出三维柱形图:
由上图可以直观地看出, 吸烟与患肺癌 .
(2) 根据列联表的数据,作出二维条形图:
由上图可以直观地看出, 吸烟与患肺癌 .
根据列联表的数据,作出等高条形图:
由上图可以直观地看出, 吸烟与患肺癌 .
反思:(独立性检验的必要性)通过数据和图形,我们得到的直观印象是患肺癌有关.那是否有一定的把握认为“吸烟与患肺癌有关”呢?
新知2:统计量吸烟与患肺癌列联表
假设:吸烟与患肺癌没关系,则在吸烟者和不吸烟者中患肺癌不患肺癌者的相应比例 .即
因此, 越小,说明吸烟与患肺癌之间关系 ;反之, .
=
探 究 案
※ 典型例题
例1 吸烟与患肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸 烟
2099
49
2148
总 计
9874
91
9965
不健康
健 康
总计
不优秀
41
626
667
优 秀
37
296
333
总 计
78
922
1000
求.
※ 动手试试
练1. 性别与喜欢数学课程列联表:
喜欢数学
不喜欢数学
总 计
男
37
85
122
女
35
143
178
总 计
72
228
300
求.
练习案
※ 当堂检测(时量:5分钟 满分:10分)计分:
1. 分类变量: .
2. 列联表: .
3. 统计量: .
※ 知识拓展
1. 分类变量的取值一定是离散的,而且不同的取值仅表示个体所属的类别,如性别变量,只取男、女两个值,商品的等级变量只取一级、二级、三级,等等. 分类变量的取值有时可用数字来表示,但这时的数字除了分类以外没有其他的含义. 如用“0”表示“男”,用“1”表示“女”.
2. 独立性检验的步骤(略)及原理(与反证法类似):
反证法
假设检验
要证明结论A
备择假设H
在A不成立的前提下进行推理
在H不成立的条件下,即H成立的条件下进行推理
推出矛盾,意味着结论A成立
推出有利于H成立的小概率事件(概率不超过的事件)发生,意味着H成立的可能性(可能性为(1-))很大
没有找到矛盾,不能对A下任何结论,即反证法不成功
推出有利于H成立的小概率事件不发生,接受原假设
课后作业
某市为调查全市高中生学习状况是否对生理健康有影响,随机进行调查并得到如下的列联表:
求.
