沪科版数学八年级上册12.2 一次函数 教案(表格式)
文档属性
| 名称 | 沪科版数学八年级上册12.2 一次函数 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 52.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 00:00:00 | ||
图片预览


文档简介
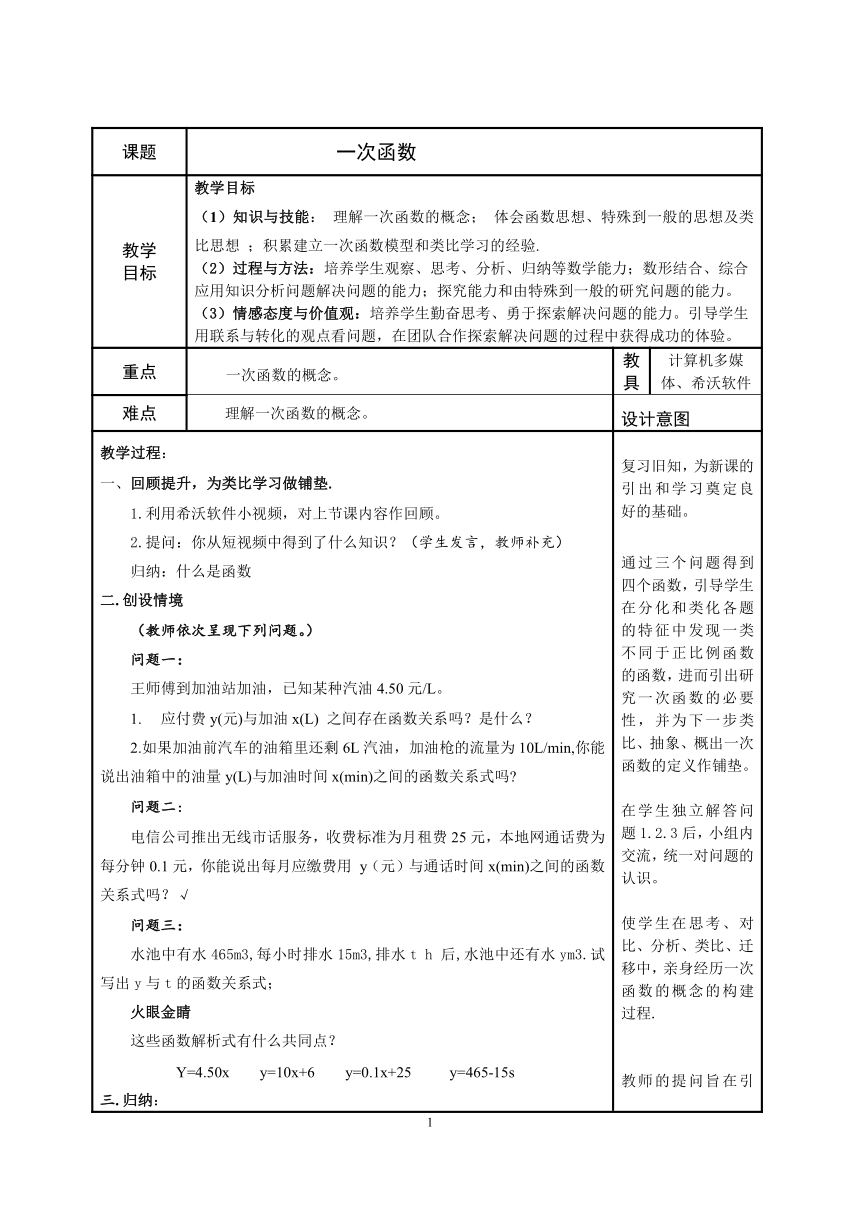
课题 一次函数
教学目标 教学目标(1)知识与技能: 理解一次函数的概念; 体会函数思想、特殊到一般的思想及类比思想 ;积累建立一次函数模型和类比学习的经验.(2)过程与方法:培养学生观察、思考、分析、归纳等数学能力;数形结合、综合应用知识分析问题解决问题的能力;探究能力和由特殊到一般的研究问题的能力。(3)情感态度与价值观:培养学生勤奋思考、勇于探索解决问题的能力。引导学生用联系与转化的观点看问题,在团队合作探索解决问题的过程中获得成功的体验。
重点 一次函数的概念。 教具 计算机多媒体、希沃软件
难点 理解一次函数的概念。 设计意图
(1)正方形面积y与边长x之间的函数关系:
(2)已知△ABC一边AB上的高为8,△ABC的面积y与△ABC的AB边x的关系.
(3)一棵树现在高5 0 厘米,每个月长高2 厘米,x 月后这棵树的高度为y 厘米。(4)圆面积S与半径r的关系。2.下列函数中哪些y是x的一次函数?并指出函数中k、b的值.y=2(x-x2)+2x2 y=(a2+1)x+5 |y|=3x y=3/x-3 y=-3x/π y=π+3.14说明:学生在独立思考基础上,小组合作完成.教师通过抽查小组最差学生的学习情况检查反馈各组学生对一次函数的概念的理解情况.五.一展身手1.设函数 y =(m-3)x3-│m│+m+2 .①当m为何值时,它是一次函数?②当m为何值时,它是正比例函数?说明:学生在独立思考基础上,小组合作完成.教师根据学生的解答过程指出,在解决实际问题时,先找到两个变量,由实际问题构建出一个一次函数模型,再用函数知识解决实际问题,这是一种函数的思想方法。2. 拖拉机开始工作时,油箱中有油36升,如果每小时耗油3升,那么油箱中余油量Y(升)与工作时间t(小时)之间的关系式是什么 工作9小时后油箱中余油量是多少 六、课堂聚焦(1)通过本节课的学习,①对自己说,你有哪些收获?②对同学说,你有哪些温馨提示?③对老师说,你有哪些困惑?说明:让学生从不同的角度、不同的侧面畅谈自己的感受,引发不同学生更深层次的思考,促进学生数学思维品质的优化。教师归纳,提升学生认识。1.一次函数的定义及注意事项。注意:(1).k、b为常数,且k≠0..x和y的次数是1.判定一个函数是否是一次函数,要从化简后来判断!数学来源于生活又反作用于生活。完成作业,在类比中拓展1.函数y=mxm-1+(m-1)是一次函数,则m值( )A.m≠0 B.m=2 C.m=2或4 D.m>22.已知,若函数y=(m-1)+3是关于x的一次函数,求m的值,并写出解析式.3.类比正比例函数的学习过程,举出一个一次函数的实例,写出它的解析式并尝试画出这个函数的图象,试探究这个函数的性质.八.师生共勉 时间是一个“常量”,但对于勤奋者来说,却是一个“变量”,我们应当在有限的时间内做出伟大的事业! 复习旧知,为新课的引出和学习奠定良好的基础。通过三个问题得到四个函数,引导学生在分化和类化各题的特征中发现一类不同于正比例函数的函数,进而引出研究一次函数的必要性,并为下一步类比、抽象、概出一次函数的定义作铺垫。在学生独立解答问题1.2.3后,小组内交流,统一对问题的认识。使学生在思考、对比、分析、类比、迁移中,亲身经历一次函数的概念的构建过程.教师的提问旨在引起学生的思维冲突,在思考中使学生理解正比例函数是特殊的一次函数.深化学生对一次函数概念的理解.遵循学生的认知规律,多角度,多层次地设置习题,在类比中应用,在应用中加深学生对一次函数概念的理解. 通过“具体——抽象——具体”的过程,使学生进一步加深对一次函数概念的认识,并在这个过程中,体会一次函数是刻画现实世界变化规律的重要数学模型,感悟函数的思想.引导在学习交流中,认识到函数是解决现实问题的重要工具,提高学习数学的自信心. 增强应用数学的意识.创设反思情境,搭建交流平台,体现人文关怀。作业1、2是为巩固对一次函数的理解,作业3是为下节课学习一次函数的图象和性质做好铺垫,同时也是类比的学习方法应用中,进一步体会“类比思想”.让学生在知识和情感上双丰收.
板书设计 一次函数 一.温故 二.创设情境 (1) 问题一 问题二 问题 三 (2)火眼金睛三、归纳四. 敲脑洞五.一展身手六、课堂聚焦七.完成作业,八.师生共勉
一、教材分析函数是近代数学最基本的概念之一,在数学发展过程中起着十分重要的作用,许多数学分支(如代数、三角、解析几何、微积分、实变函数、复变函数等)都是以函数为中心展开研究的。一次函数属于《数学课程标准》中“数与代数”领域,是最基本的、最简单的函数.一次函数的概念是本章的重点。教材在前面首先安排了函数的内容,讨论了函数的定义,接着本节学习一次函数的定义它既是对函数概念的进一步理解,又是特殊的一次函数——正比例函数到一般的一次函数的拓展,它还是今后继续学习“用函数观点看方程(组)与不等式”的基础,在本章中起着承上启下的作用.它也是将来学习二次函数,反比例函数的基础。本节教学内容还是学生进一步体会“函数思想”“类比思想”“数形结合思想”的很好素材。
二、学情分析本节课是以类比的思想方法为主线,研究什么是一次函数. 这是在学生学习了函数的定义,并初步了解了如何研究一个具体函数(从定义到图象与性质)的基础上学习的。学生原有知识与学习经验对本节课的类比学习奠定扎实的学习基础,在前后知识的类比学习中,学生可以进一步理解函数的知识,体验研究函数的基本思路,促进学生的认知结构的不断的完善,进而发展学生的类比、抽象与概括能力.而这些目标的达成必须是在充分发挥学生的主体作用,给予学生足够的活动、探究、交流、反思的时间与空间,让在学生在类比中学习、在类比中思考的前提下才能完成的。
三.教学反思在自己的教学中就此涉及到的知识点有了温习,设计讲解练习也做到循序渐进。在学生练习时利用课堂活动.时间设置,让整个课堂充满激情。教学有序。不足之处:不能放开,把课堂完全交给学生 ,学生活动的时间短,时间分配不当,在以后的教学中一定要多多注意,争取有所提高。同时,对西沃白板的熟悉程度有待提高。争取在以后的教学中多用,让教学效果更显突出。
1
教学目标 教学目标(1)知识与技能: 理解一次函数的概念; 体会函数思想、特殊到一般的思想及类比思想 ;积累建立一次函数模型和类比学习的经验.(2)过程与方法:培养学生观察、思考、分析、归纳等数学能力;数形结合、综合应用知识分析问题解决问题的能力;探究能力和由特殊到一般的研究问题的能力。(3)情感态度与价值观:培养学生勤奋思考、勇于探索解决问题的能力。引导学生用联系与转化的观点看问题,在团队合作探索解决问题的过程中获得成功的体验。
重点 一次函数的概念。 教具 计算机多媒体、希沃软件
难点 理解一次函数的概念。 设计意图
(1)正方形面积y与边长x之间的函数关系:
(2)已知△ABC一边AB上的高为8,△ABC的面积y与△ABC的AB边x的关系.
(3)一棵树现在高5 0 厘米,每个月长高2 厘米,x 月后这棵树的高度为y 厘米。(4)圆面积S与半径r的关系。2.下列函数中哪些y是x的一次函数?并指出函数中k、b的值.y=2(x-x2)+2x2 y=(a2+1)x+5 |y|=3x y=3/x-3 y=-3x/π y=π+3.14说明:学生在独立思考基础上,小组合作完成.教师通过抽查小组最差学生的学习情况检查反馈各组学生对一次函数的概念的理解情况.五.一展身手1.设函数 y =(m-3)x3-│m│+m+2 .①当m为何值时,它是一次函数?②当m为何值时,它是正比例函数?说明:学生在独立思考基础上,小组合作完成.教师根据学生的解答过程指出,在解决实际问题时,先找到两个变量,由实际问题构建出一个一次函数模型,再用函数知识解决实际问题,这是一种函数的思想方法。2. 拖拉机开始工作时,油箱中有油36升,如果每小时耗油3升,那么油箱中余油量Y(升)与工作时间t(小时)之间的关系式是什么 工作9小时后油箱中余油量是多少 六、课堂聚焦(1)通过本节课的学习,①对自己说,你有哪些收获?②对同学说,你有哪些温馨提示?③对老师说,你有哪些困惑?说明:让学生从不同的角度、不同的侧面畅谈自己的感受,引发不同学生更深层次的思考,促进学生数学思维品质的优化。教师归纳,提升学生认识。1.一次函数的定义及注意事项。注意:(1).k、b为常数,且k≠0..x和y的次数是1.判定一个函数是否是一次函数,要从化简后来判断!数学来源于生活又反作用于生活。完成作业,在类比中拓展1.函数y=mxm-1+(m-1)是一次函数,则m值( )A.m≠0 B.m=2 C.m=2或4 D.m>22.已知,若函数y=(m-1)+3是关于x的一次函数,求m的值,并写出解析式.3.类比正比例函数的学习过程,举出一个一次函数的实例,写出它的解析式并尝试画出这个函数的图象,试探究这个函数的性质.八.师生共勉 时间是一个“常量”,但对于勤奋者来说,却是一个“变量”,我们应当在有限的时间内做出伟大的事业! 复习旧知,为新课的引出和学习奠定良好的基础。通过三个问题得到四个函数,引导学生在分化和类化各题的特征中发现一类不同于正比例函数的函数,进而引出研究一次函数的必要性,并为下一步类比、抽象、概出一次函数的定义作铺垫。在学生独立解答问题1.2.3后,小组内交流,统一对问题的认识。使学生在思考、对比、分析、类比、迁移中,亲身经历一次函数的概念的构建过程.教师的提问旨在引起学生的思维冲突,在思考中使学生理解正比例函数是特殊的一次函数.深化学生对一次函数概念的理解.遵循学生的认知规律,多角度,多层次地设置习题,在类比中应用,在应用中加深学生对一次函数概念的理解. 通过“具体——抽象——具体”的过程,使学生进一步加深对一次函数概念的认识,并在这个过程中,体会一次函数是刻画现实世界变化规律的重要数学模型,感悟函数的思想.引导在学习交流中,认识到函数是解决现实问题的重要工具,提高学习数学的自信心. 增强应用数学的意识.创设反思情境,搭建交流平台,体现人文关怀。作业1、2是为巩固对一次函数的理解,作业3是为下节课学习一次函数的图象和性质做好铺垫,同时也是类比的学习方法应用中,进一步体会“类比思想”.让学生在知识和情感上双丰收.
板书设计 一次函数 一.温故 二.创设情境 (1) 问题一 问题二 问题 三 (2)火眼金睛三、归纳四. 敲脑洞五.一展身手六、课堂聚焦七.完成作业,八.师生共勉
一、教材分析函数是近代数学最基本的概念之一,在数学发展过程中起着十分重要的作用,许多数学分支(如代数、三角、解析几何、微积分、实变函数、复变函数等)都是以函数为中心展开研究的。一次函数属于《数学课程标准》中“数与代数”领域,是最基本的、最简单的函数.一次函数的概念是本章的重点。教材在前面首先安排了函数的内容,讨论了函数的定义,接着本节学习一次函数的定义它既是对函数概念的进一步理解,又是特殊的一次函数——正比例函数到一般的一次函数的拓展,它还是今后继续学习“用函数观点看方程(组)与不等式”的基础,在本章中起着承上启下的作用.它也是将来学习二次函数,反比例函数的基础。本节教学内容还是学生进一步体会“函数思想”“类比思想”“数形结合思想”的很好素材。
二、学情分析本节课是以类比的思想方法为主线,研究什么是一次函数. 这是在学生学习了函数的定义,并初步了解了如何研究一个具体函数(从定义到图象与性质)的基础上学习的。学生原有知识与学习经验对本节课的类比学习奠定扎实的学习基础,在前后知识的类比学习中,学生可以进一步理解函数的知识,体验研究函数的基本思路,促进学生的认知结构的不断的完善,进而发展学生的类比、抽象与概括能力.而这些目标的达成必须是在充分发挥学生的主体作用,给予学生足够的活动、探究、交流、反思的时间与空间,让在学生在类比中学习、在类比中思考的前提下才能完成的。
三.教学反思在自己的教学中就此涉及到的知识点有了温习,设计讲解练习也做到循序渐进。在学生练习时利用课堂活动.时间设置,让整个课堂充满激情。教学有序。不足之处:不能放开,把课堂完全交给学生 ,学生活动的时间短,时间分配不当,在以后的教学中一定要多多注意,争取有所提高。同时,对西沃白板的熟悉程度有待提高。争取在以后的教学中多用,让教学效果更显突出。
1
