苏科版七年级数学下册 11.5 用一元一次不等式解决问题 学案(表格式)
文档属性
| 名称 | 苏科版七年级数学下册 11.5 用一元一次不等式解决问题 学案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 00:00:00 | ||
图片预览

文档简介
第十一章《一元一次不等式》 导学案
课题 11.5用一元一次不等式解决问题(1)
学习目标: 1、了解利用不等式解决问题的一般步骤; 2、初步学会用一元一次不等式的模型解决实际问题。 教师复备及学生学习笔记
重难点:1.重点: 掌握用不的呢过是解题的一般步骤。 2.难点: 根据题意,列出不等式。
教学法:自主学习,讨论,讲练结合
导 学 过 程
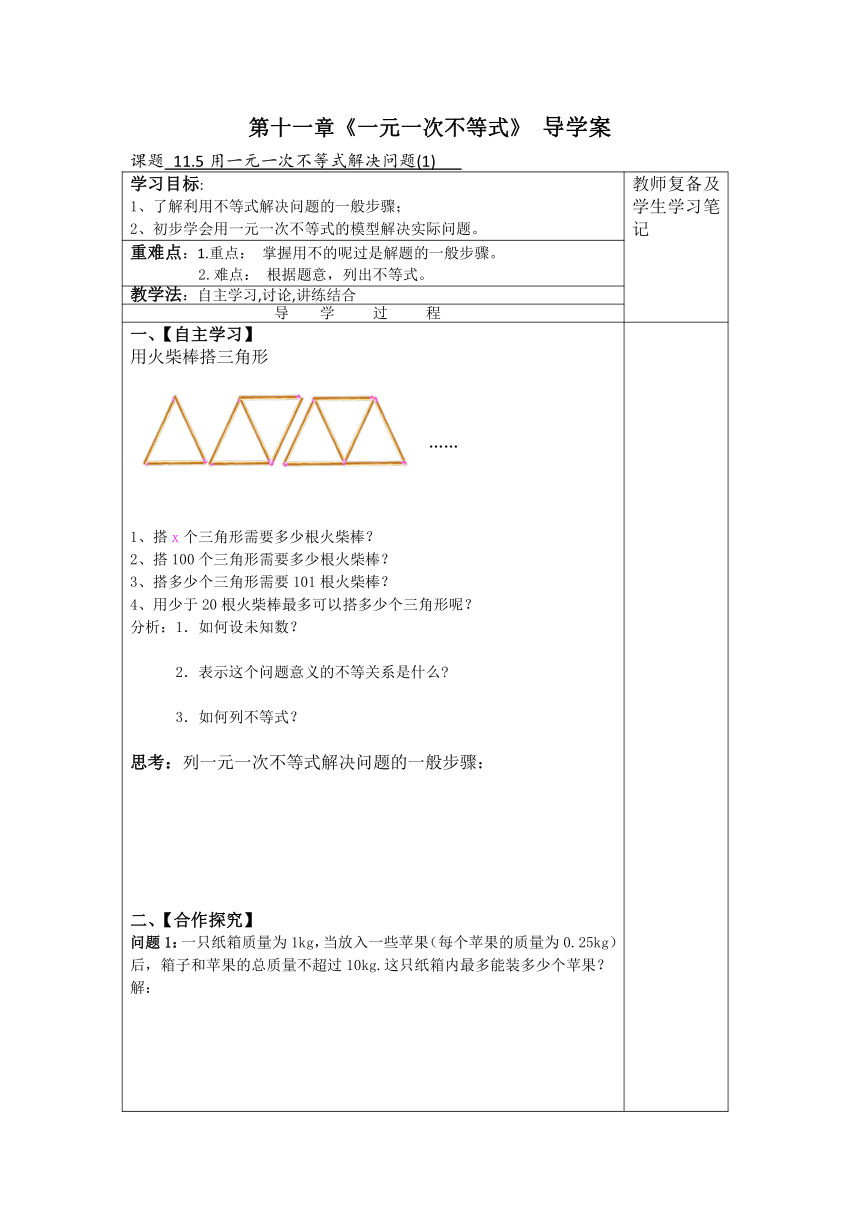
一、【自主学习】 用火柴棒搭三角形 …… 1、搭x个三角形需要多少根火柴棒? 2、搭100个三角形需要多少根火柴棒? 3、搭多少个三角形需要101根火柴棒? 4、用少于20根火柴棒最多可以搭多少个三角形呢? 分析:1.如何设未知数? 2.表示这个问题意义的不等关系是什么 3.如何列不等式? 思考:列一元一次不等式解决问题的一般步骤: 二、【合作探究】 问题1:一只纸箱质量为1kg,当放入一些苹果(每个苹果的质量为0.25kg)后,箱子和苹果的总质量不超过10kg.这只纸箱内最多能装多少个苹果? 解: 问题2:某种杜鹃花适宜生长在平均气温为17℃到20 ℃ 之间的山区。已知某山区山脚下的平均气温为20 ℃,并且每上升100m,气温下降0.6 ℃ ,求该山区适宜种植这种杜鹃花的山坡的高度 ? 三、【基础训练】 1.一个n 边形的内角和比它的外角和至少大120度,n的最小值是多少? (1)本题的不等关系是:_______________________. (2) 根据题意,得一元一次不等式:___________________. 2.某茶叶店销售一批袋装茶叶,第一个月以50元/袋的价格售出80袋,第二个月以40元/袋的价格将这批茶叶全部售出,销售收入不超过8000元。这批茶叶最多有多少袋? 本题的不等关系是:____________________. (2)设_________________,根据题意,得一元一次不等式: ___________________. 3.某工程队计划在10天内整修河堤600m。施工2天修了120m后,该工程需要比原计划提前2天完成,此后平均每天至少要整修河堤多少米? (1) 本题的不等关系是:_____________________. (2) 设______________________________,根据题意, 得一元一次不等式:______________________________. 4.某电影院暑假向学生优惠开放,每张票2元.另外,每场次还可以售出每张5元的普通票300张,如果要保持每场次票房收入不低于2000元,那么平均每场次至少应出售学生优惠票多少张? 四、【思维拓展】 暑假学校准备组织一批学生参加夏令营,联系了甲、乙两家旅行社,他们的服务质量相同,且入营费都是每人200元.经过协商,甲旅行社表示可以给每位入营队员七五折优惠;乙旅行社表示可先免去一位带队老师的费用,其余的入营队员八折优惠.请问应该选择哪家旅行社,才能使费用最少? 五、【当堂检测】 1.甲、乙两队进行足球对抗赛,比赛规则规定每队胜一场得3分,平一场得1分,负一场得0分.两队一共比赛了10场,甲队保持不败,得分超过22分.甲队至少胜了多少场? 2.解答第132页“数学实验室”中的问题。
六、【课堂小结】 1.一元一次不等式解决问题有哪些步骤? 2.用一元一次不等式解决问题的关键是什么?
七、【作业布置】:《伴你学》相应练习
八、【自主反思】:
课题 11.5用一元一次不等式解决问题(1)
学习目标: 1、了解利用不等式解决问题的一般步骤; 2、初步学会用一元一次不等式的模型解决实际问题。 教师复备及学生学习笔记
重难点:1.重点: 掌握用不的呢过是解题的一般步骤。 2.难点: 根据题意,列出不等式。
教学法:自主学习,讨论,讲练结合
导 学 过 程
一、【自主学习】 用火柴棒搭三角形 …… 1、搭x个三角形需要多少根火柴棒? 2、搭100个三角形需要多少根火柴棒? 3、搭多少个三角形需要101根火柴棒? 4、用少于20根火柴棒最多可以搭多少个三角形呢? 分析:1.如何设未知数? 2.表示这个问题意义的不等关系是什么 3.如何列不等式? 思考:列一元一次不等式解决问题的一般步骤: 二、【合作探究】 问题1:一只纸箱质量为1kg,当放入一些苹果(每个苹果的质量为0.25kg)后,箱子和苹果的总质量不超过10kg.这只纸箱内最多能装多少个苹果? 解: 问题2:某种杜鹃花适宜生长在平均气温为17℃到20 ℃ 之间的山区。已知某山区山脚下的平均气温为20 ℃,并且每上升100m,气温下降0.6 ℃ ,求该山区适宜种植这种杜鹃花的山坡的高度 ? 三、【基础训练】 1.一个n 边形的内角和比它的外角和至少大120度,n的最小值是多少? (1)本题的不等关系是:_______________________. (2) 根据题意,得一元一次不等式:___________________. 2.某茶叶店销售一批袋装茶叶,第一个月以50元/袋的价格售出80袋,第二个月以40元/袋的价格将这批茶叶全部售出,销售收入不超过8000元。这批茶叶最多有多少袋? 本题的不等关系是:____________________. (2)设_________________,根据题意,得一元一次不等式: ___________________. 3.某工程队计划在10天内整修河堤600m。施工2天修了120m后,该工程需要比原计划提前2天完成,此后平均每天至少要整修河堤多少米? (1) 本题的不等关系是:_____________________. (2) 设______________________________,根据题意, 得一元一次不等式:______________________________. 4.某电影院暑假向学生优惠开放,每张票2元.另外,每场次还可以售出每张5元的普通票300张,如果要保持每场次票房收入不低于2000元,那么平均每场次至少应出售学生优惠票多少张? 四、【思维拓展】 暑假学校准备组织一批学生参加夏令营,联系了甲、乙两家旅行社,他们的服务质量相同,且入营费都是每人200元.经过协商,甲旅行社表示可以给每位入营队员七五折优惠;乙旅行社表示可先免去一位带队老师的费用,其余的入营队员八折优惠.请问应该选择哪家旅行社,才能使费用最少? 五、【当堂检测】 1.甲、乙两队进行足球对抗赛,比赛规则规定每队胜一场得3分,平一场得1分,负一场得0分.两队一共比赛了10场,甲队保持不败,得分超过22分.甲队至少胜了多少场? 2.解答第132页“数学实验室”中的问题。
六、【课堂小结】 1.一元一次不等式解决问题有哪些步骤? 2.用一元一次不等式解决问题的关键是什么?
七、【作业布置】:《伴你学》相应练习
八、【自主反思】:
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
