人教版九年级数学上册22.3实际问题与二次函数 教学设计
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 200.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 10:39:29 | ||
图片预览

文档简介
实际问题与二次函数教学设计
教学目标
知识技能
通过探究实际问题与二次函数关系,让学生掌握利用顶点坐标解决最大值(或最小值)问题的方法.
数学思考
1.通过研究生活中实际问题,让学生体会建立数学建模的思想.
2.通过学习和探究“矩形面积”“销售利润”问题,渗透转化及分类的数学思想方法.
解决问题
通过研究生活中实际问题,体会数学知识的现实意义,进一步认识如何利用二次函数的有关知识解决实际问题.
情感态度
通过将“二次函数的最大值”的知识灵活用于实际,让学生亲自体会到学习数学的价值,从而提高学生学习数学的兴趣.
重点
探究利用二次函数的最大值(或最小值)解决实际问题的方法.
难点
如何将实际问题转化为二次函数的问题.
教师教学方法:情境法,引导法,问题法,练习法
学生学习方法:讨论法,练习法
教 学 课 程 设 计
一.知识回顾
2、图中所示的二次函数图像的解析式为:
二新课探索
问题与情境1
通过运用函数模型让学生体会数学的实际价值,学会用函数的观点认识问题,解决问题.体会应在自变量取值范围内求函数的最值。
让学生在合作学习中共同解决问题,培养学生的合作精神.
问题情景2:
单价(元) 20 x
销售量(件) 500 500+100〖20-x〗
单件利润(元) 20-5 x-5
总利润(元) (20-5)×500 (x-5)〖500+100(20-x)〗
设销售单价为x,总利润为y,则:
y=(x-5)〖500+100(20-x)〗
练习
某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个。
(1)假设销售单价提高x元,那么销售每个篮球所获得的利润是 ( )元;这种篮球每月的销售量是
( )个(用含x的代数式表示)。
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,
请你求出最大利润,此时篮球的售价应定为多少元?
课堂小结
通过本节课的学习你有何启发与收获?
1、求下列二次函数的最大值或最小值:
(2)y=2x2+8x+13
(1)y=-x2+4x;
-2
0
2
4
6
2
-4
x
y
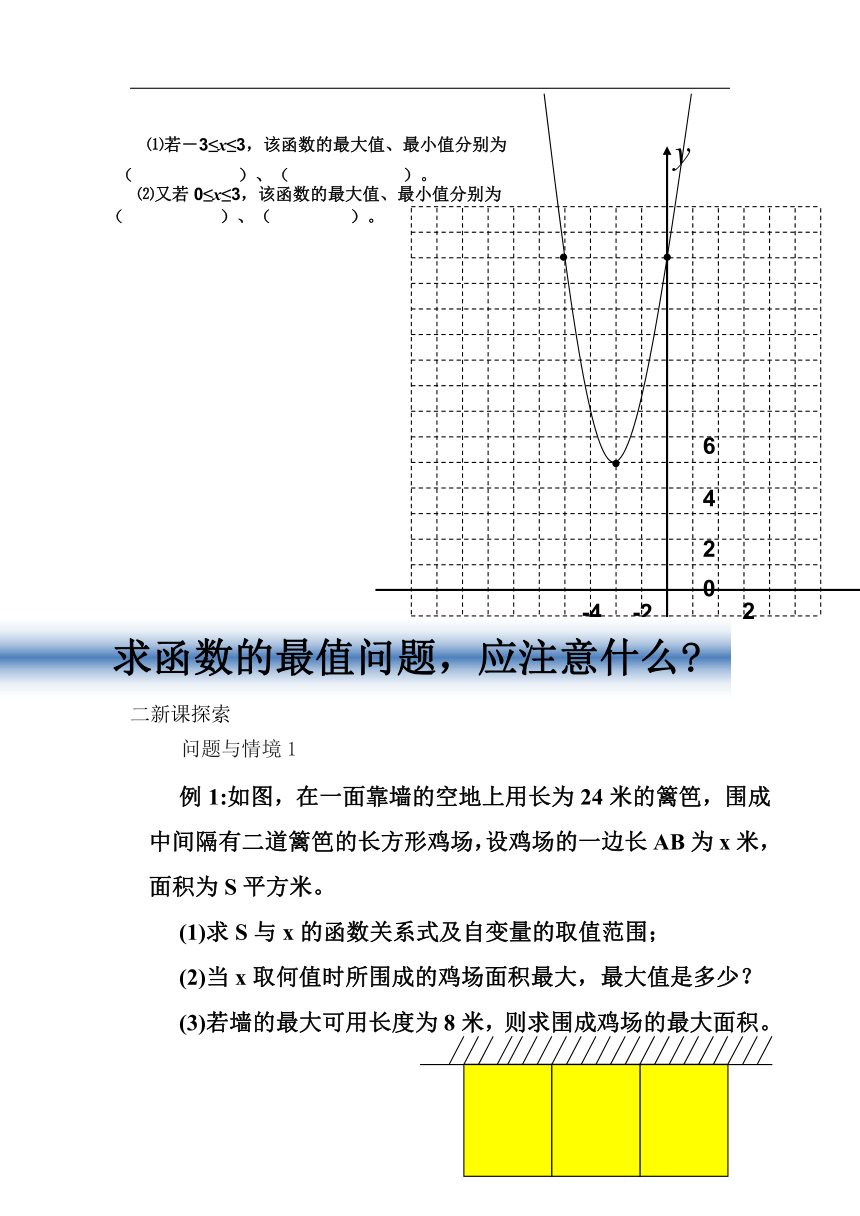
⑴若-3≤x≤3,该函数的最大值、最小值分别为( )、( )。
⑵又若0≤x≤3,该函数的最大值、最小值分别为( )、( )。
求函数的最值问题,应注意什么
例1:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形鸡场,设鸡场的一边长AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的鸡场面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成鸡场的最大面积。
A
例2.某商店经营T恤衫,已知成批购进时单价是5元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是20元时,销售量是500件;而单价每降低1元,就可以多售出100件。
请你帮助分析,销售单价是多少时,可以获利最多?
即
y= -100(x-15) +10000
所以当x=15时,y有最大值10000.
即单价为15元,获最大利润10000元。
教学目标
知识技能
通过探究实际问题与二次函数关系,让学生掌握利用顶点坐标解决最大值(或最小值)问题的方法.
数学思考
1.通过研究生活中实际问题,让学生体会建立数学建模的思想.
2.通过学习和探究“矩形面积”“销售利润”问题,渗透转化及分类的数学思想方法.
解决问题
通过研究生活中实际问题,体会数学知识的现实意义,进一步认识如何利用二次函数的有关知识解决实际问题.
情感态度
通过将“二次函数的最大值”的知识灵活用于实际,让学生亲自体会到学习数学的价值,从而提高学生学习数学的兴趣.
重点
探究利用二次函数的最大值(或最小值)解决实际问题的方法.
难点
如何将实际问题转化为二次函数的问题.
教师教学方法:情境法,引导法,问题法,练习法
学生学习方法:讨论法,练习法
教 学 课 程 设 计
一.知识回顾
2、图中所示的二次函数图像的解析式为:
二新课探索
问题与情境1
通过运用函数模型让学生体会数学的实际价值,学会用函数的观点认识问题,解决问题.体会应在自变量取值范围内求函数的最值。
让学生在合作学习中共同解决问题,培养学生的合作精神.
问题情景2:
单价(元) 20 x
销售量(件) 500 500+100〖20-x〗
单件利润(元) 20-5 x-5
总利润(元) (20-5)×500 (x-5)〖500+100(20-x)〗
设销售单价为x,总利润为y,则:
y=(x-5)〖500+100(20-x)〗
练习
某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个。
(1)假设销售单价提高x元,那么销售每个篮球所获得的利润是 ( )元;这种篮球每月的销售量是
( )个(用含x的代数式表示)。
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,
请你求出最大利润,此时篮球的售价应定为多少元?
课堂小结
通过本节课的学习你有何启发与收获?
1、求下列二次函数的最大值或最小值:
(2)y=2x2+8x+13
(1)y=-x2+4x;
-2
0
2
4
6
2
-4
x
y
⑴若-3≤x≤3,该函数的最大值、最小值分别为( )、( )。
⑵又若0≤x≤3,该函数的最大值、最小值分别为( )、( )。
求函数的最值问题,应注意什么
例1:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形鸡场,设鸡场的一边长AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的鸡场面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成鸡场的最大面积。
A
例2.某商店经营T恤衫,已知成批购进时单价是5元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是20元时,销售量是500件;而单价每降低1元,就可以多售出100件。
请你帮助分析,销售单价是多少时,可以获利最多?
即
y= -100(x-15) +10000
所以当x=15时,y有最大值10000.
即单价为15元,获最大利润10000元。
同课章节目录
