27.2.1相似三角形的判定(第二课时边边边) -
文档属性
| 名称 | 27.2.1相似三角形的判定(第二课时边边边) - |  | |
| 格式 | zip | ||
| 文件大小 | 225.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-19 21:04:48 | ||
图片预览



文档简介
课件13张PPT。 §27.2.1相似三角形的判定
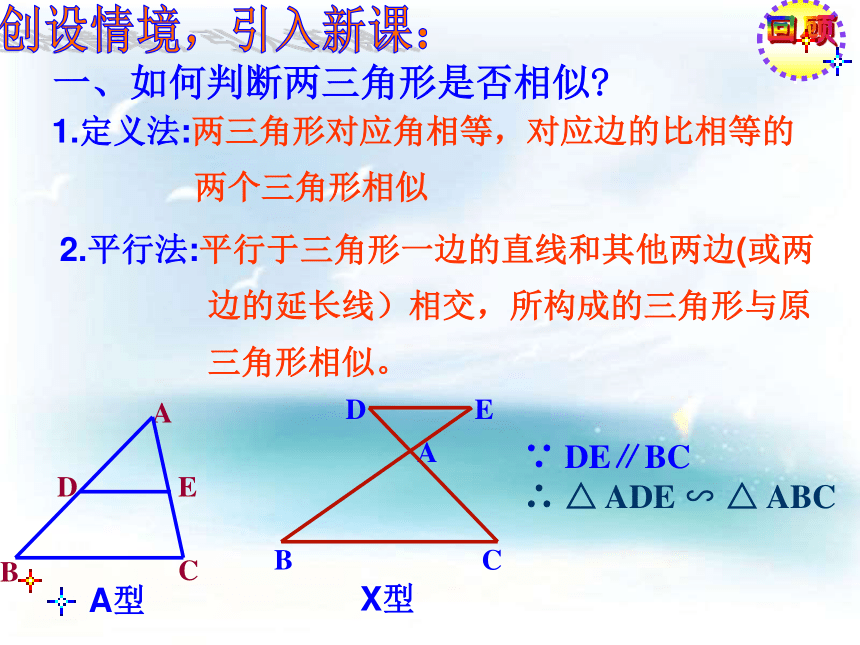
(第2课时)1.定义法:两三角形对应角相等,对应边的比相等的
两个三角形相似回顾一、如何判断两三角形是否相似? ∵ DE∥BC
∴ △ ADE ∽ △ ABC A型X型创设情境,引入新课:2.平行法:平行于三角形一边的直线和其他两边(或两
边的延长线)相交,所构成的三角形与原
三角形相似。猜想? 有没有其他简单的办法判断两个三角形相似呢? 二、 三角形全等有哪几种简单的判
定方法呢?SSS、SAS 、ASA(AAS)、HL探究1
任意画一个三角形,再利用尺规作图再画一个三角形,使它的各边长都是原来三角形各边长的k倍。
(1)这两个三角形的对应角相等吗?
(2)这两个三角形相似吗?
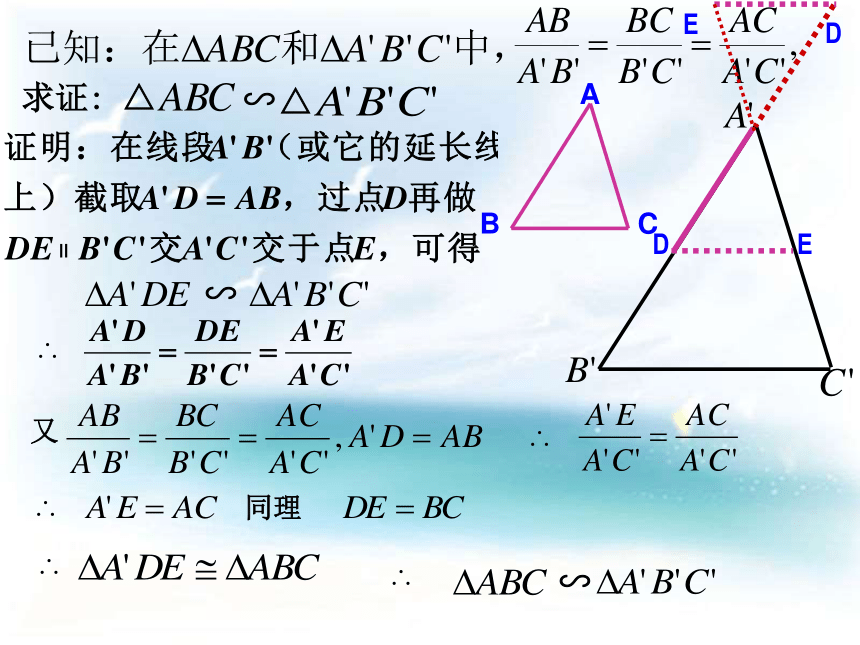
(3)由此你能得出什么样的结论?命题:
如果两个三角形的三组对应边的比相等,
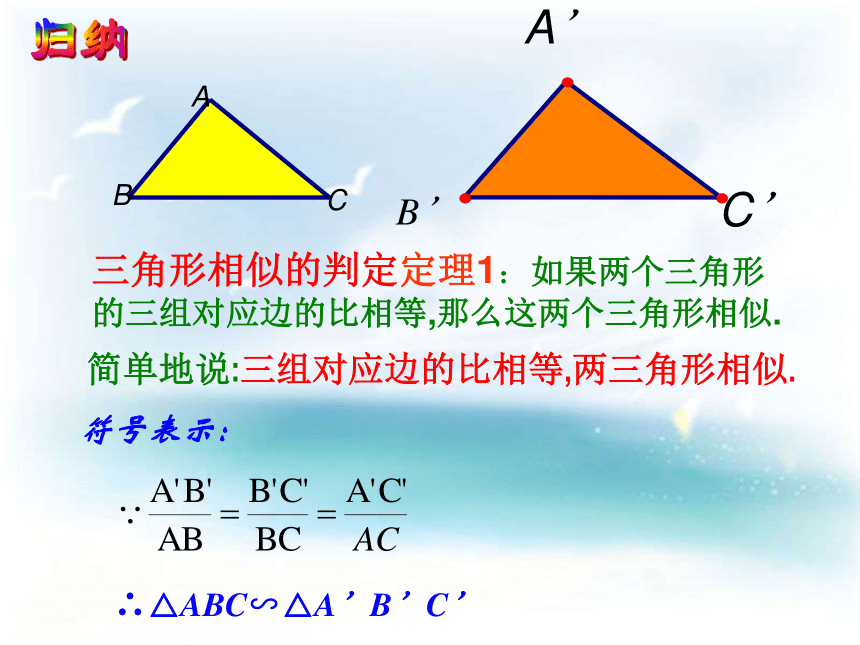
那么这两个三角形相似.DE∴又∴同理 ∴∽∴DE归纳∴△ABC∽△A’B’C’ 三角形相似的判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.简单地说:三组对应边的比相等,两三角形相似.符号表示:学以致用: 1:根据下列条件,试判定△ABC与△A′B′C′是否相似,并说明理由.
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
(2) AB=12cm, BC=15cm, AC=24cm
A’B’=40cm,B’C’=16cm,A’C’=20cm2、(1)判断图中两个三角形是否相似?
15 20 27 40
25 45∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE巩固提高:要制作两个形状相同的三角形框架,其中一 个三角形框架的三边长分别为4,6,8。另一个三角形框架的一边长为2,它的另外两条边长应当是多少?你有几种答案?提示:三种选法,分别使另一个三角形的长
为2的边与长为4,6,8的边对应。2:4=x:6=y:8
x:4=2:6=y:8
x:4=y:6=2:8挑战自我:相似三角形的判定方法:小结小结:1、定义判定法3、边边边判定法2、平行判定法比较复杂,烦琐只能在特定的图形里面使用本节课你有什么收获?学习的方法:主要的有类比、转化作业:P54页 习题27.2
第2题(1,2),第3题.
(第2课时)1.定义法:两三角形对应角相等,对应边的比相等的
两个三角形相似回顾一、如何判断两三角形是否相似? ∵ DE∥BC
∴ △ ADE ∽ △ ABC A型X型创设情境,引入新课:2.平行法:平行于三角形一边的直线和其他两边(或两
边的延长线)相交,所构成的三角形与原
三角形相似。猜想? 有没有其他简单的办法判断两个三角形相似呢? 二、 三角形全等有哪几种简单的判
定方法呢?SSS、SAS 、ASA(AAS)、HL探究1
任意画一个三角形,再利用尺规作图再画一个三角形,使它的各边长都是原来三角形各边长的k倍。
(1)这两个三角形的对应角相等吗?
(2)这两个三角形相似吗?
(3)由此你能得出什么样的结论?命题:
如果两个三角形的三组对应边的比相等,
那么这两个三角形相似.DE∴又∴同理 ∴∽∴DE归纳∴△ABC∽△A’B’C’ 三角形相似的判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.简单地说:三组对应边的比相等,两三角形相似.符号表示:学以致用: 1:根据下列条件,试判定△ABC与△A′B′C′是否相似,并说明理由.
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
(2) AB=12cm, BC=15cm, AC=24cm
A’B’=40cm,B’C’=16cm,A’C’=20cm2、(1)判断图中两个三角形是否相似?
15 20 27 40
25 45∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE巩固提高:要制作两个形状相同的三角形框架,其中一 个三角形框架的三边长分别为4,6,8。另一个三角形框架的一边长为2,它的另外两条边长应当是多少?你有几种答案?提示:三种选法,分别使另一个三角形的长
为2的边与长为4,6,8的边对应。2:4=x:6=y:8
x:4=2:6=y:8
x:4=y:6=2:8挑战自我:相似三角形的判定方法:小结小结:1、定义判定法3、边边边判定法2、平行判定法比较复杂,烦琐只能在特定的图形里面使用本节课你有什么收获?学习的方法:主要的有类比、转化作业:P54页 习题27.2
第2题(1,2),第3题.
