7.1.2平面直角坐标系(第2课时) 课件(共43张PPT)
文档属性
| 名称 | 7.1.2平面直角坐标系(第2课时) 课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 18:55:31 | ||
图片预览








文档简介
(共43张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第七章 平面直角坐标系
7.1.2 平面直角坐标系
第2课时
1.理解各象限内及坐标轴上点的坐标特征.
2.会用象限说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
学习目标
在平面内画两条_________、_________的数轴,组成平面直角坐标系.
______的数轴称为 x 轴或横轴.
______的数轴称为 y 轴或纵轴.
两坐标轴的交点为平面直角坐
标系的_____.
互相垂直
原点重合
水平
竖直
原点
x
O
y
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
回顾旧知
如图,在平面直角坐标系中,
(1) 写出 A,B,C 三点的坐标;
(2) 描出点 D(4,-1),E(-1,2),F(1,0).
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
4
B
C
D
(3,4)
(-4,0)
(-3,-2)
E
F
A
思考 原点 O 的坐标是什么?x 轴和 y 轴上的点的坐标有什么特点?
新知 直角坐标系中点的坐标的特征
合作探究
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
(0,2)
(0,-3)
(3,0)
(-3,0)
(0,0)
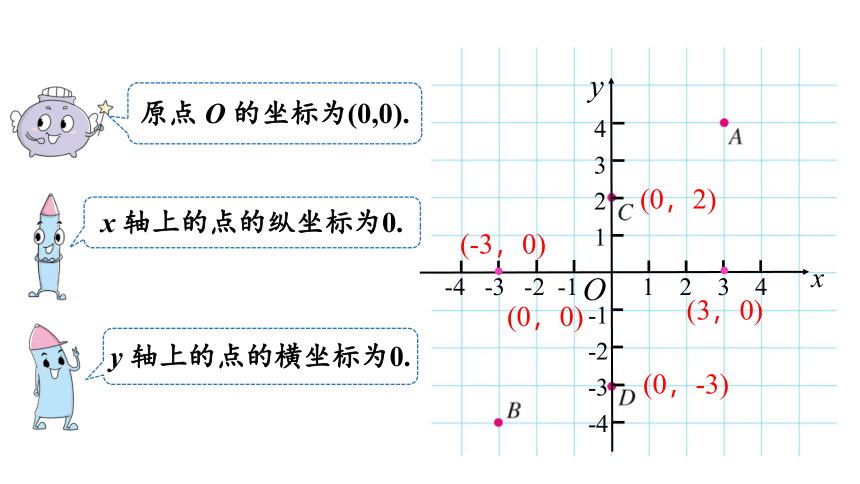
原点 O 的坐标为(0,0).
x 轴上的点的纵坐标为0.
y 轴上的点的横坐标为0.
x
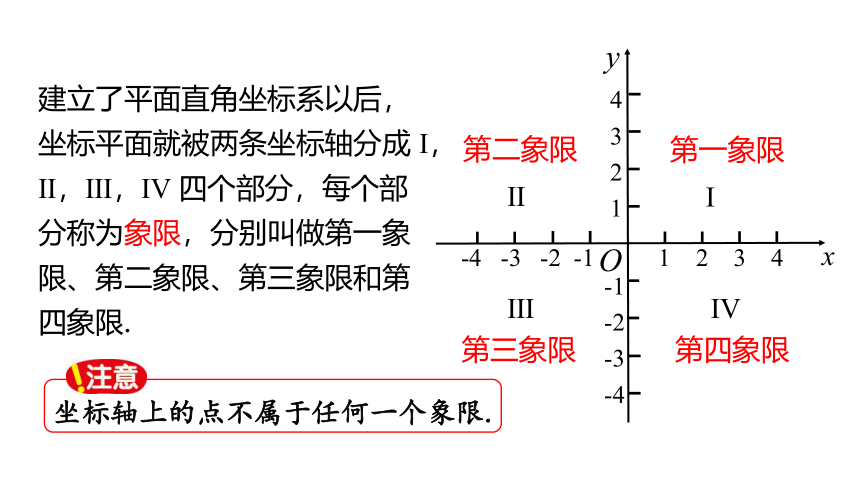
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成 Ⅰ,Ⅱ,Ⅲ,Ⅳ 四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不属于任何一个象限.
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
x
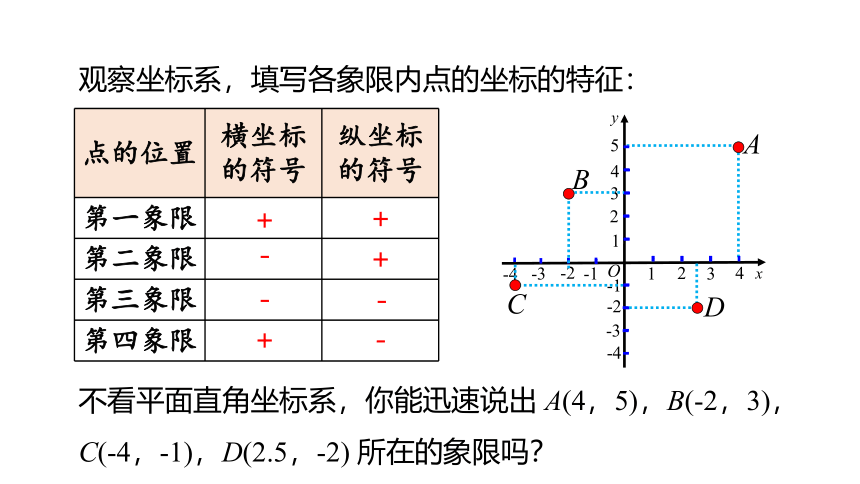
观察坐标系,填写各象限内点的坐标的特征:
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
不看平面直角坐标系,你能迅速说出 A(4,5),B(-2,3),C(-4,-1),D(2.5,-2) 所在的象限吗?
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
点的位置 横坐标的符号(或值) 纵坐标的
符号(或值)
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
0
+
+
-
-
0
0
0
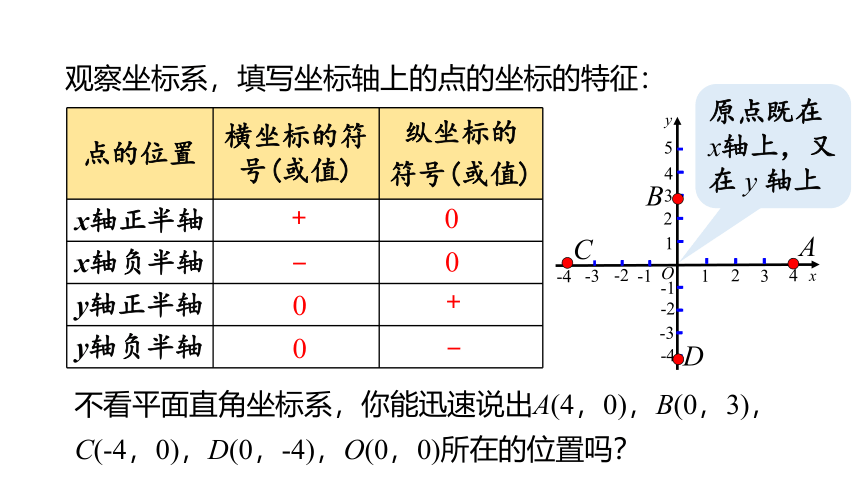
不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),C(-4,0),D(0,-4),O(0,0)所在的位置吗?
A
B
C
D
观察坐标系,填写坐标轴上的点的坐标的特征:
原点既在 x轴上,又在 y 轴上
1.第一、三象限角平分线上的点的横、纵坐标相等;第二、四象限角平分线上的点的横、纵坐标互为相反数.
2.与 x (y)轴平行的直线上的点的纵(横)坐标相同.
1. x 轴上的点的纵坐标为 0,y 轴上的点的横坐标为 0.
2.横、纵坐标的符号(或值)决定了这个点所在的象限(或坐标轴).
例 已知点 M(3a-9,a-1).
(1)若点 M 在 y 轴上,求点 M 的坐标;
解:(1)∵ 点 M 在 y 轴上,
∴ 3a-9=0,解得 a=3,
∴ a-1 =2,
∴ 点 M 的坐标为(0,2).
例 已知点 M(3a-9,a-1).
(2)若点 M 在第二、四象限的角平分线上,求点 M 的坐标;
解:(2) ∵ 点 M 在第二、四象限的角平分线上,
∴ 3a-9+a-1=0,解得 a=2.5,
∴ 3a-9= -1.5,a-1=1.5,
∴ 点 M 的坐标为( -1.5,1.5).
例 已知点 M(3a-9,a-1).
(3)若点 M 的纵坐标比横坐标大 4,求点 M 的坐标.
解:(3)由题意可知,a-1 -(3a-9) =4,解得 a=2,
∴ 3a-9=-3,a-1=l,
∴ 点 M 的坐标为( -3,1).
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
解:如图,以顶点 A 为原点,AB 所
在直线为 x 轴,AD 所在直线为 y 轴建
立平面直角坐标系.
4
4
y
x
(A)
B
C
D
O
此时,正方形四个顶点 A、B、C、D 的坐
标分别为:A(0,0),B(4,0),C(4,4), D(0,4).
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
A
B
C
D
请另建一个平面直角坐标系,看看此时正方形的四个顶点 A,B,C,D 的坐标分别是多少.
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(0,-4),B(4,-4),C(4,0),D(0,0).
解:如图,以顶点 D 为原点,DC 所
在直线为 x 轴,AD 所在直线为 y 轴建
立平面直角坐标系.
-4
4
y
x
A
B
C
(D)
O
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(-4,-4),B(0,-4),C(0,0),D(-4,0).
解:如图,以顶点 C 为原点,DC 所
在直线为 x 轴,BC 所在直线为 y 轴建
立平面直角坐标系.
-4
-4
y
x
A
B
(C)
D
O
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(-4,0),B(0,0),C(0,4),D(-4,4).
解:如图,以顶点 B 为原点,AB 所
在直线为 x 轴,BC 所在直线为 y 轴建
立平面直角坐标系.
-4
4
y
x
A
(B)
C
D
O
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
解:如图,以正方形 ABCD 的中心为原点,过中心平行于 AB 的直线为 x 轴,过中心平行于 AD 的直线为 y 轴建立平面直角坐标系.
-2
2
y
x
A
B
C
D
O
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(-2,-2),B(2,-2),C(2,2),D(-2,2).
-2
2
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
几何图形中建立适当的平面直角坐标系的技巧
1.使图形中尽量多的点在坐标轴上;
2.以某些特殊线段所在的直线为 x 轴或 y 轴;
3.若图形被一条直线分得的两部分形状、大小相同,则可以将此直线作为 x 轴或 y 轴;
4.以某已知点为原点,使它的坐标为(0,0).
如图,小手盖住的点的坐标可能为( )
A. (5,2)
B. (-6,3)
C. (-4,-6)
D. (3,-4)
第四象限
横坐标为正,
纵坐标为负
D
巩固新知
1.在平面直角坐标系中,点 A(-2,3)位于哪个象限?( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
B
课堂练习
2.在平面直角坐标系的第二象限内有一点 M,点 M 到 x 轴的距离为 3,到 y 轴的距离为 4,则点 M 的坐标是( )
A. (3,-4) B. (4,-3)
C. (-4,3) D. (-3,4)
横坐标为负,纵坐标为正
纵坐标为3
横坐标为-4
C
3.已知点 A 的坐标为(a+1,3-a),下列说法正确的是( )
A.若点 A 在 y 轴上,则 a=3
B.若点 A 在第一、三象限角平分线上,则 a=1
C.若点 A 到 x 轴的距离是 3,则 a=±6
D.若点 A 在第四象限,则 a 的值可以为 -2
a+1=0
a=-1
a+1=3-a
a=1
|3-a|=3
a=6或0
3-a>0
不在第四象限
B
象限内点的坐标符号特征
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
归纳新知
坐标轴上点的坐标符号特征
点的位置 横坐标的符号(或值) 纵坐标的
符号(或值)
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
0
+
+
-
-
0
0
0
1.下列说法正确的是( )
A.平面内,两条互相垂直的直线构成数轴
B.坐标为(3,4)与(4,3)表示同一个点
C.x轴上的点必是纵坐标为0,横坐标不为0
D.坐标原点不属于任何象限
D
课后练习
2.如图,点A(-2,1)到y轴的距离为( )
C
3.在平面直角坐标系中描出下列各组中的点,并将各组内的点用线段依次连接起来.
(1)A(-3,-3),B(0,-1),C(0,-4);
(2)A′(-4,0),B′(3,0),C′(0,5),D′(-2,3).
解:描点连线略
4.下列坐标平面内的点,在第三象限的是( )
A.(1,2) B.(-1,-2)
C.(-1,2) D.(1,-2)
5.在平面直角坐标系中,点P(0,2)在( )
A.x轴上 B.y轴上
C.第三象限 D.第四象限
B
B
6.(2020·滨州中考)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标是( )
A.(-4,5) B.(-5,4)
C.(4,-5) D.(5,-4)
D
7.(2020·金华)点P(m,2)在第二象限内,则m的值可以是___________
_____________________________(写出一个即可).
8.若点A(a+3,a-1)在x轴上,那么点A的坐标是_______________.
-1(答案不唯一)
(4,0)
9.已知:点P(2m+4,m-1),试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
解:(1)令2m+4=0,解得m=-2,所以P点的坐标为(0,-3)
(2)令m-1=0,解得m=1,所以P点的坐标为(6,0)
(3)令m-1=(2m+4)+3,解得m=-8,所以P点的坐标为(-12,-9)
10.(2020·扬州)在平面直角坐标系中,点P(x2+2,-3)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
11.(2020·黄冈)在平面直角坐标系中,若点A(a,-b)在第三象限,则点B(-ab,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
A
12.已知AB∥y轴,点A的坐标为(3,2),并且AB=5,则点B的坐标为__ _______________________.
13.在平面直角坐标系中,点P(m-3,4-2m)不可能在第____象限.
(3,7)或(3,-3)
一
14.△ABC在平面直角坐标系中的位置如图所示.
(1)A,B,C三点的坐标分别为___________________________________;
(2)在图中依次描出下列各点,并用线段按顺序把它们连接起来:(1,-4),(1,-5),(2,-5),(2,-1);
(3)图中的三角形与你所画的折线组合成一个什么图形?
(2,1),(-1,-1),(5,-1)
15.如图,如果用(0,0)表示点A,(1,0)表示点B,(1,2)表示点F.请按照这个规律表示出其它点的坐标.
∴C(2,0),D(2,1),E(2,2),G(0,2),H(0,1)
16.已知点M(3a-2,a+6),分别根据下列条件求出M点的坐标.
(1)点M在y轴上;
(2)点N的坐标为(-4,6),直线MN∥x轴;
(3)点M到x轴、y轴的距离相等.
17.如图,点A(3,1),B(3,-3),C(-1,-2).
(1)A,B两点之间的距离为____;
(2)点C到x轴的距离为____,到y轴的距离为____;
(3)求△ABC的面积;
(4)点P在x轴上,当△ABP的面积为10时,求点P的坐标.
4
2
1
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第七章 平面直角坐标系
7.1.2 平面直角坐标系
第2课时
1.理解各象限内及坐标轴上点的坐标特征.
2.会用象限说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
学习目标
在平面内画两条_________、_________的数轴,组成平面直角坐标系.
______的数轴称为 x 轴或横轴.
______的数轴称为 y 轴或纵轴.
两坐标轴的交点为平面直角坐
标系的_____.
互相垂直
原点重合
水平
竖直
原点
x
O
y
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
回顾旧知
如图,在平面直角坐标系中,
(1) 写出 A,B,C 三点的坐标;
(2) 描出点 D(4,-1),E(-1,2),F(1,0).
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
4
B
C
D
(3,4)
(-4,0)
(-3,-2)
E
F
A
思考 原点 O 的坐标是什么?x 轴和 y 轴上的点的坐标有什么特点?
新知 直角坐标系中点的坐标的特征
合作探究
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
(0,2)
(0,-3)
(3,0)
(-3,0)
(0,0)
原点 O 的坐标为(0,0).
x 轴上的点的纵坐标为0.
y 轴上的点的横坐标为0.
x
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成 Ⅰ,Ⅱ,Ⅲ,Ⅳ 四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不属于任何一个象限.
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
x
观察坐标系,填写各象限内点的坐标的特征:
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
不看平面直角坐标系,你能迅速说出 A(4,5),B(-2,3),C(-4,-1),D(2.5,-2) 所在的象限吗?
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
点的位置 横坐标的符号(或值) 纵坐标的
符号(或值)
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
0
+
+
-
-
0
0
0
不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),C(-4,0),D(0,-4),O(0,0)所在的位置吗?
A
B
C
D
观察坐标系,填写坐标轴上的点的坐标的特征:
原点既在 x轴上,又在 y 轴上
1.第一、三象限角平分线上的点的横、纵坐标相等;第二、四象限角平分线上的点的横、纵坐标互为相反数.
2.与 x (y)轴平行的直线上的点的纵(横)坐标相同.
1. x 轴上的点的纵坐标为 0,y 轴上的点的横坐标为 0.
2.横、纵坐标的符号(或值)决定了这个点所在的象限(或坐标轴).
例 已知点 M(3a-9,a-1).
(1)若点 M 在 y 轴上,求点 M 的坐标;
解:(1)∵ 点 M 在 y 轴上,
∴ 3a-9=0,解得 a=3,
∴ a-1 =2,
∴ 点 M 的坐标为(0,2).
例 已知点 M(3a-9,a-1).
(2)若点 M 在第二、四象限的角平分线上,求点 M 的坐标;
解:(2) ∵ 点 M 在第二、四象限的角平分线上,
∴ 3a-9+a-1=0,解得 a=2.5,
∴ 3a-9= -1.5,a-1=1.5,
∴ 点 M 的坐标为( -1.5,1.5).
例 已知点 M(3a-9,a-1).
(3)若点 M 的纵坐标比横坐标大 4,求点 M 的坐标.
解:(3)由题意可知,a-1 -(3a-9) =4,解得 a=2,
∴ 3a-9=-3,a-1=l,
∴ 点 M 的坐标为( -3,1).
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
解:如图,以顶点 A 为原点,AB 所
在直线为 x 轴,AD 所在直线为 y 轴建
立平面直角坐标系.
4
4
y
x
(A)
B
C
D
O
此时,正方形四个顶点 A、B、C、D 的坐
标分别为:A(0,0),B(4,0),C(4,4), D(0,4).
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
A
B
C
D
请另建一个平面直角坐标系,看看此时正方形的四个顶点 A,B,C,D 的坐标分别是多少.
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(0,-4),B(4,-4),C(4,0),D(0,0).
解:如图,以顶点 D 为原点,DC 所
在直线为 x 轴,AD 所在直线为 y 轴建
立平面直角坐标系.
-4
4
y
x
A
B
C
(D)
O
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(-4,-4),B(0,-4),C(0,0),D(-4,0).
解:如图,以顶点 C 为原点,DC 所
在直线为 x 轴,BC 所在直线为 y 轴建
立平面直角坐标系.
-4
-4
y
x
A
B
(C)
D
O
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(-4,0),B(0,0),C(0,4),D(-4,4).
解:如图,以顶点 B 为原点,AB 所
在直线为 x 轴,BC 所在直线为 y 轴建
立平面直角坐标系.
-4
4
y
x
A
(B)
C
D
O
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
解:如图,以正方形 ABCD 的中心为原点,过中心平行于 AB 的直线为 x 轴,过中心平行于 AD 的直线为 y 轴建立平面直角坐标系.
-2
2
y
x
A
B
C
D
O
此时,正方形四个顶点 A,B,C,D 的坐
标分别为:A(-2,-2),B(2,-2),C(2,2),D(-2,2).
-2
2
探究 正方形 ABCD 的边长为 4,请建立一个平面直角坐标系,并写出正方形的四个顶点 A,B,C,D 在这个平面直角坐标系中的坐标.
几何图形中建立适当的平面直角坐标系的技巧
1.使图形中尽量多的点在坐标轴上;
2.以某些特殊线段所在的直线为 x 轴或 y 轴;
3.若图形被一条直线分得的两部分形状、大小相同,则可以将此直线作为 x 轴或 y 轴;
4.以某已知点为原点,使它的坐标为(0,0).
如图,小手盖住的点的坐标可能为( )
A. (5,2)
B. (-6,3)
C. (-4,-6)
D. (3,-4)
第四象限
横坐标为正,
纵坐标为负
D
巩固新知
1.在平面直角坐标系中,点 A(-2,3)位于哪个象限?( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
B
课堂练习
2.在平面直角坐标系的第二象限内有一点 M,点 M 到 x 轴的距离为 3,到 y 轴的距离为 4,则点 M 的坐标是( )
A. (3,-4) B. (4,-3)
C. (-4,3) D. (-3,4)
横坐标为负,纵坐标为正
纵坐标为3
横坐标为-4
C
3.已知点 A 的坐标为(a+1,3-a),下列说法正确的是( )
A.若点 A 在 y 轴上,则 a=3
B.若点 A 在第一、三象限角平分线上,则 a=1
C.若点 A 到 x 轴的距离是 3,则 a=±6
D.若点 A 在第四象限,则 a 的值可以为 -2
a+1=0
a=-1
a+1=3-a
a=1
|3-a|=3
a=6或0
3-a>0
不在第四象限
B
象限内点的坐标符号特征
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
归纳新知
坐标轴上点的坐标符号特征
点的位置 横坐标的符号(或值) 纵坐标的
符号(或值)
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
0
+
+
-
-
0
0
0
1.下列说法正确的是( )
A.平面内,两条互相垂直的直线构成数轴
B.坐标为(3,4)与(4,3)表示同一个点
C.x轴上的点必是纵坐标为0,横坐标不为0
D.坐标原点不属于任何象限
D
课后练习
2.如图,点A(-2,1)到y轴的距离为( )
C
3.在平面直角坐标系中描出下列各组中的点,并将各组内的点用线段依次连接起来.
(1)A(-3,-3),B(0,-1),C(0,-4);
(2)A′(-4,0),B′(3,0),C′(0,5),D′(-2,3).
解:描点连线略
4.下列坐标平面内的点,在第三象限的是( )
A.(1,2) B.(-1,-2)
C.(-1,2) D.(1,-2)
5.在平面直角坐标系中,点P(0,2)在( )
A.x轴上 B.y轴上
C.第三象限 D.第四象限
B
B
6.(2020·滨州中考)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标是( )
A.(-4,5) B.(-5,4)
C.(4,-5) D.(5,-4)
D
7.(2020·金华)点P(m,2)在第二象限内,则m的值可以是___________
_____________________________(写出一个即可).
8.若点A(a+3,a-1)在x轴上,那么点A的坐标是_______________.
-1(答案不唯一)
(4,0)
9.已知:点P(2m+4,m-1),试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
解:(1)令2m+4=0,解得m=-2,所以P点的坐标为(0,-3)
(2)令m-1=0,解得m=1,所以P点的坐标为(6,0)
(3)令m-1=(2m+4)+3,解得m=-8,所以P点的坐标为(-12,-9)
10.(2020·扬州)在平面直角坐标系中,点P(x2+2,-3)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
11.(2020·黄冈)在平面直角坐标系中,若点A(a,-b)在第三象限,则点B(-ab,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
A
12.已知AB∥y轴,点A的坐标为(3,2),并且AB=5,则点B的坐标为__ _______________________.
13.在平面直角坐标系中,点P(m-3,4-2m)不可能在第____象限.
(3,7)或(3,-3)
一
14.△ABC在平面直角坐标系中的位置如图所示.
(1)A,B,C三点的坐标分别为___________________________________;
(2)在图中依次描出下列各点,并用线段按顺序把它们连接起来:(1,-4),(1,-5),(2,-5),(2,-1);
(3)图中的三角形与你所画的折线组合成一个什么图形?
(2,1),(-1,-1),(5,-1)
15.如图,如果用(0,0)表示点A,(1,0)表示点B,(1,2)表示点F.请按照这个规律表示出其它点的坐标.
∴C(2,0),D(2,1),E(2,2),G(0,2),H(0,1)
16.已知点M(3a-2,a+6),分别根据下列条件求出M点的坐标.
(1)点M在y轴上;
(2)点N的坐标为(-4,6),直线MN∥x轴;
(3)点M到x轴、y轴的距离相等.
17.如图,点A(3,1),B(3,-3),C(-1,-2).
(1)A,B两点之间的距离为____;
(2)点C到x轴的距离为____,到y轴的距离为____;
(3)求△ABC的面积;
(4)点P在x轴上,当△ABP的面积为10时,求点P的坐标.
4
2
1
https://www.21cnjy.com/help/help_extract.php
