27.2.2 相似三角形的性质 同步练习(含答案)
文档属性
| 名称 | 27.2.2 相似三角形的性质 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 20:02:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十七章 相 似
27.2 相似三角形
27.2.2 相似三角形的性质
1. 若△ABC∽△DEF,相似比为4∶3,则△ABC与△DEF对应的中线之比为( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
2. 如果两个相似三角形的对应边上的高之比为1∶3,则这两个三角形的面积比为( )
A.2∶3 B.1∶3 C.1∶9 D.1∶
3. 有两个相似的三角形,已知其中一个三角形的最长边为12 cm,面积为18 cm2,而另一个三角形的最长边为16 cm,则其面积是( )
A.22 cm2 B.24 cm2 C.30 cm2 D.32 cm2
4. 已知△ABC与△DEF相似且对应周长比为4∶3,则△ABC与△DEF的面积比为( )
A.8∶3 B.16∶81 C.9∶16 D.16∶9
5. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为( )
A.105° B.115° C.125° D.135°
6. 如图,△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2.下列等式一定成立的是( )
A.= B.= C.= D.=
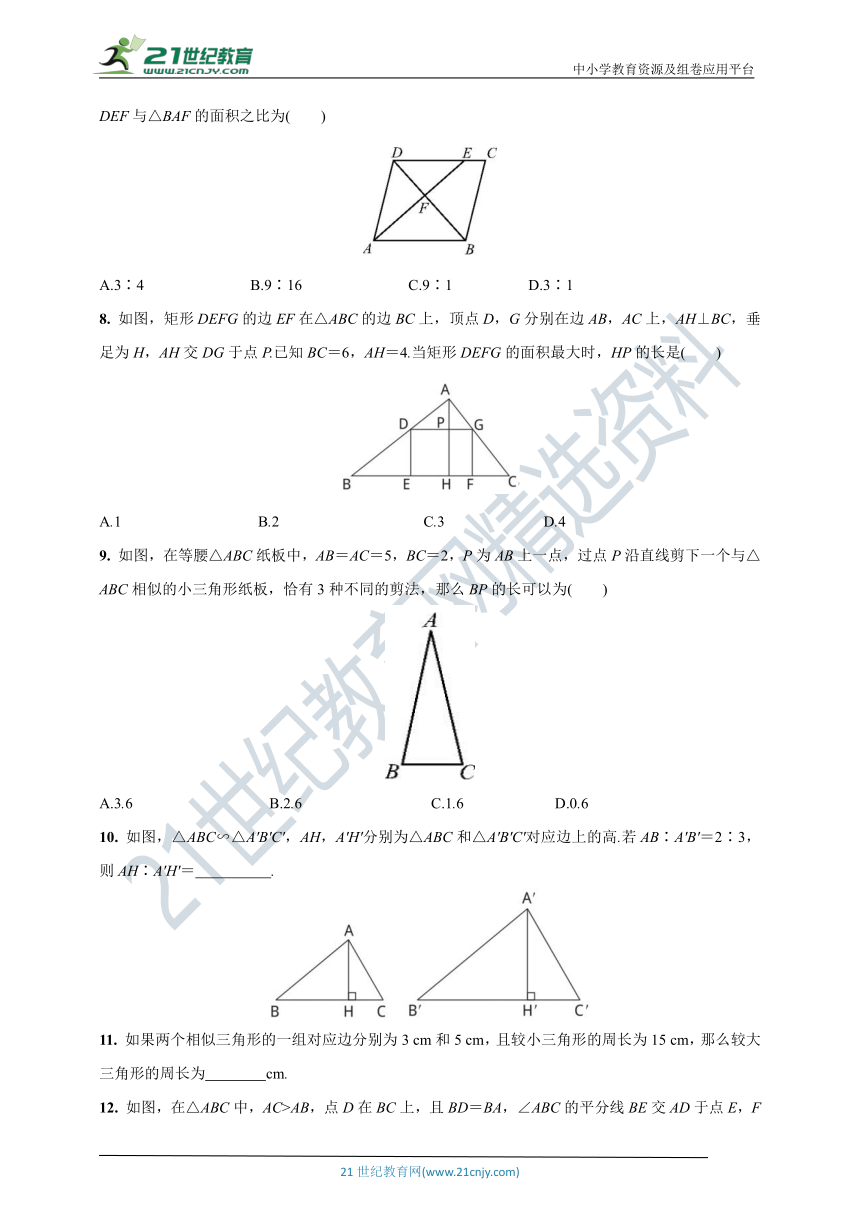
7. 如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )
A.3∶4 B.9∶16 C.9∶1 D.3∶1
8. 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P.已知BC=6,AH=4.当矩形DEFG的面积最大时,HP的长是( )
A.1 B.2 C.3 D.4
9. 如图,在等腰△ABC纸板中,AB=AC=5,BC=2,P为AB上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,恰有3种不同的剪法,那么BP的长可以为( )
A.3.6 B.2.6 C.1.6 D.0.6
10. 如图,△ABC∽△A'B'C',AH,A'H'分别为△ABC和△A'B'C'对应边上的高.若AB∶A'B'=2∶3,则AH∶A'H'= .
11. 如果两个相似三角形的一组对应边分别为3 cm和5 cm,且较小三角形的周长为15 cm,那么较大三角形的周长为 cm.
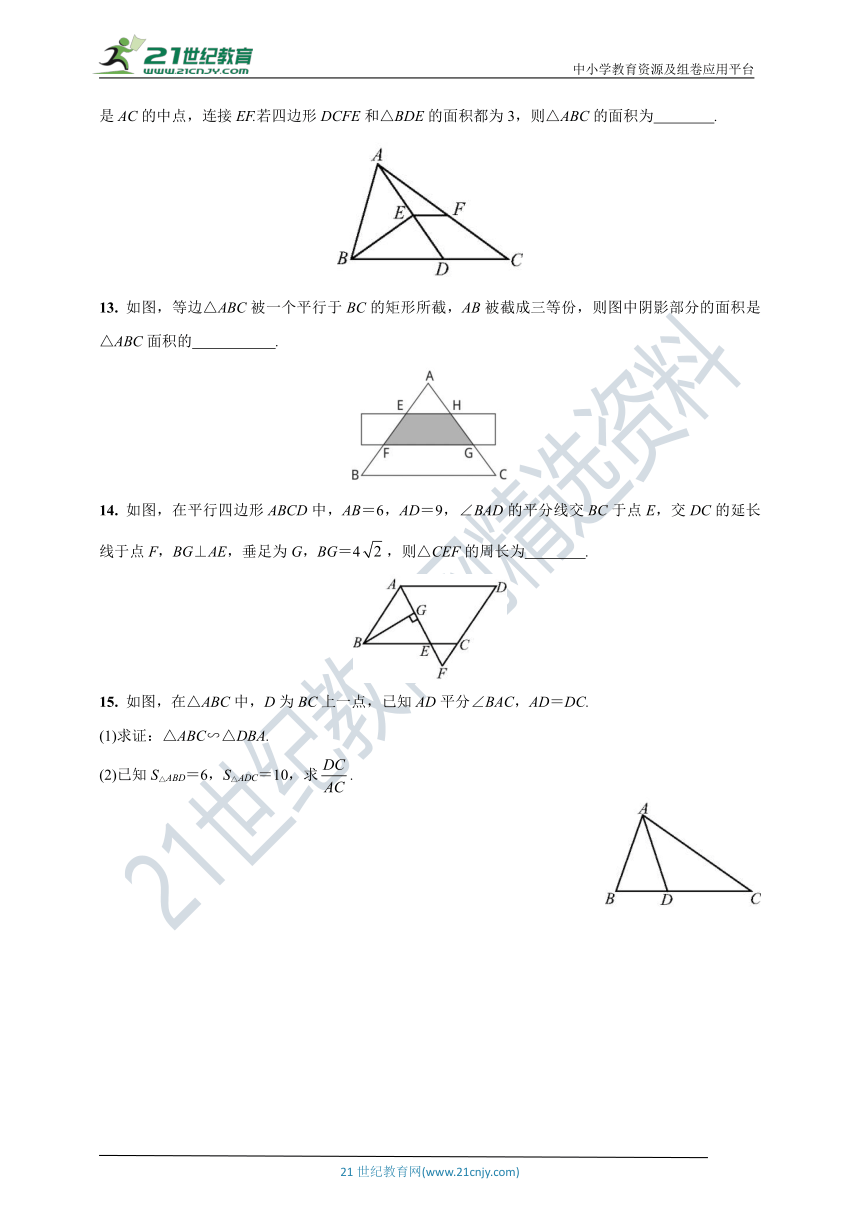
12. 如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,F是AC的中点,连接EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 .
13. 如图,等边△ABC被一个平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积是△ABC面积的 .
14. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4,则△CEF的周长为 .
15. 如图,在△ABC中,D为BC上一点,已知AD平分∠BAC,AD=DC.
(1)求证:△ABC∽△DBA.
(2)已知S△ABD=6,S△ADC=10,求.
16. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的解析式及点E的坐标;
(2)F是OC边上一点,若△FBC∽△DEB,求点F的坐标.
参 考 答 案
1. A 2. C 3. D 4. D 5. D 6. D 7. B 8. B 9. D
10. 2∶3
11. 25
12. 10
13.
14. 8
15. 解:(1)∵AD平分∠BAC,∴∠BAD=∠CAD.∵AD=DC,∴∠C=∠CAD,∴∠C=∠BAD.∵∠B=∠B,∴△ABC∽△DBA.
(2)由(1)可知△ABC∽△DBA,∴=()2.∵S△ABD=6,S△ADC=10,∴=,∴()2=,∴=.∵AD=DC,∴=.
16. 解:(1)由题意得点D的坐标为(1,3),代入反比例函数y=(x>0),得k=1×3=3,所以反比例函数的解析式为y=.当x=2时,y=,所以点E的坐标为(2,).
(2)易知BD=1,BE=,BC=2,OC=3.因为△FBC∽△DEB,所以=,即=,所以CF=,所以OF=OC-CF=,所以点F的坐标为(0,).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十七章 相 似
27.2 相似三角形
27.2.2 相似三角形的性质
1. 若△ABC∽△DEF,相似比为4∶3,则△ABC与△DEF对应的中线之比为( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
2. 如果两个相似三角形的对应边上的高之比为1∶3,则这两个三角形的面积比为( )
A.2∶3 B.1∶3 C.1∶9 D.1∶
3. 有两个相似的三角形,已知其中一个三角形的最长边为12 cm,面积为18 cm2,而另一个三角形的最长边为16 cm,则其面积是( )
A.22 cm2 B.24 cm2 C.30 cm2 D.32 cm2
4. 已知△ABC与△DEF相似且对应周长比为4∶3,则△ABC与△DEF的面积比为( )
A.8∶3 B.16∶81 C.9∶16 D.16∶9
5. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为( )
A.105° B.115° C.125° D.135°
6. 如图,△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2.下列等式一定成立的是( )
A.= B.= C.= D.=
7. 如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )
A.3∶4 B.9∶16 C.9∶1 D.3∶1
8. 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P.已知BC=6,AH=4.当矩形DEFG的面积最大时,HP的长是( )
A.1 B.2 C.3 D.4
9. 如图,在等腰△ABC纸板中,AB=AC=5,BC=2,P为AB上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,恰有3种不同的剪法,那么BP的长可以为( )
A.3.6 B.2.6 C.1.6 D.0.6
10. 如图,△ABC∽△A'B'C',AH,A'H'分别为△ABC和△A'B'C'对应边上的高.若AB∶A'B'=2∶3,则AH∶A'H'= .
11. 如果两个相似三角形的一组对应边分别为3 cm和5 cm,且较小三角形的周长为15 cm,那么较大三角形的周长为 cm.
12. 如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,F是AC的中点,连接EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 .
13. 如图,等边△ABC被一个平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积是△ABC面积的 .
14. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4,则△CEF的周长为 .
15. 如图,在△ABC中,D为BC上一点,已知AD平分∠BAC,AD=DC.
(1)求证:△ABC∽△DBA.
(2)已知S△ABD=6,S△ADC=10,求.
16. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的解析式及点E的坐标;
(2)F是OC边上一点,若△FBC∽△DEB,求点F的坐标.
参 考 答 案
1. A 2. C 3. D 4. D 5. D 6. D 7. B 8. B 9. D
10. 2∶3
11. 25
12. 10
13.
14. 8
15. 解:(1)∵AD平分∠BAC,∴∠BAD=∠CAD.∵AD=DC,∴∠C=∠CAD,∴∠C=∠BAD.∵∠B=∠B,∴△ABC∽△DBA.
(2)由(1)可知△ABC∽△DBA,∴=()2.∵S△ABD=6,S△ADC=10,∴=,∴()2=,∴=.∵AD=DC,∴=.
16. 解:(1)由题意得点D的坐标为(1,3),代入反比例函数y=(x>0),得k=1×3=3,所以反比例函数的解析式为y=.当x=2时,y=,所以点E的坐标为(2,).
(2)易知BD=1,BE=,BC=2,OC=3.因为△FBC∽△DEB,所以=,即=,所以CF=,所以OF=OC-CF=,所以点F的坐标为(0,).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
