27.2.3 相似三角形应用举例 同步练习(含答案)
文档属性
| 名称 | 27.2.3 相似三角形应用举例 同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 08:44:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十七章 相 似
27.2 相似三角形
27.2.3 相似三角形应用举例
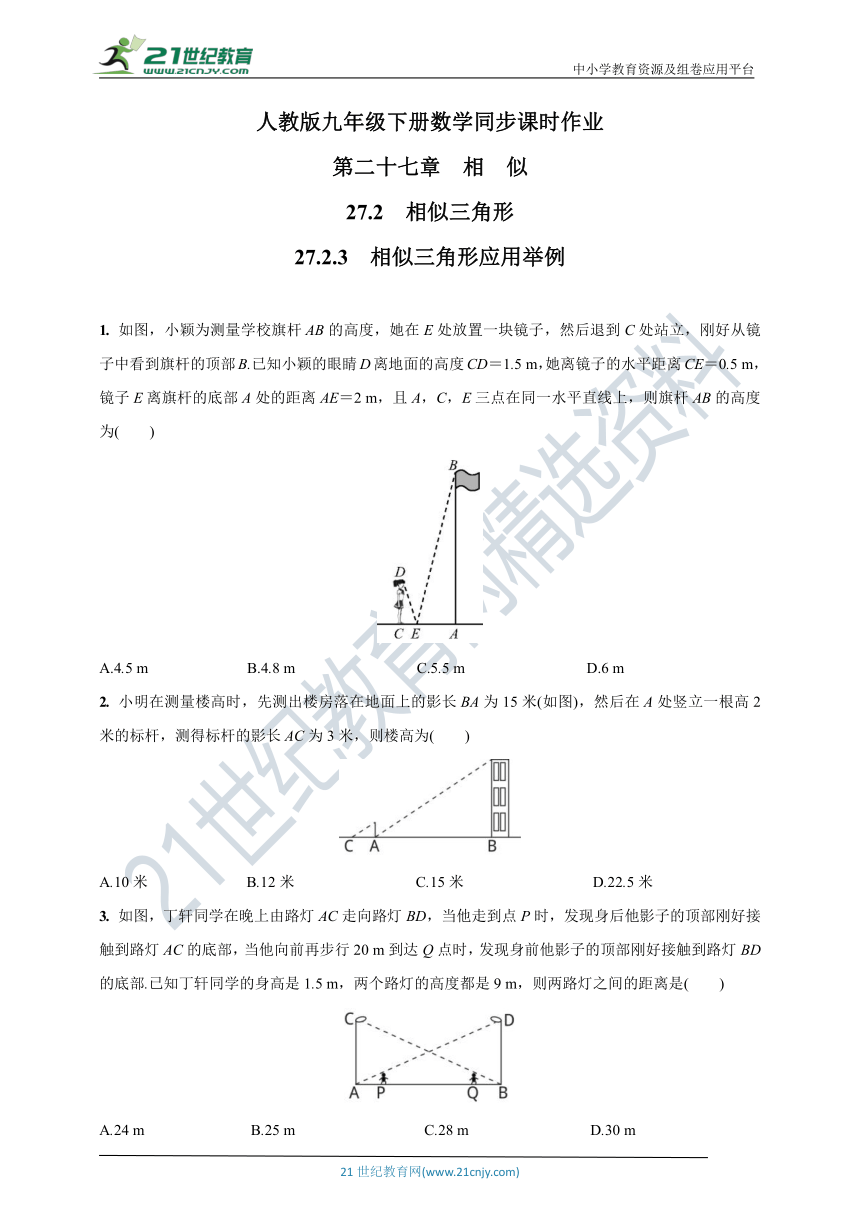
1. 如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5 m,她离镜子的水平距离CE=0.5 m,镜子E离旗杆的底部A处的距离AE=2 m,且A,C,E三点在同一水平直线上,则旗杆AB的高度为( )
A.4.5 m B.4.8 m C.5.5 m D.6 m
2. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处竖立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米 B.12米 C.15米 D.22.5米
3. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是( )
A.24 m B.25 m C.28 m D.30 m
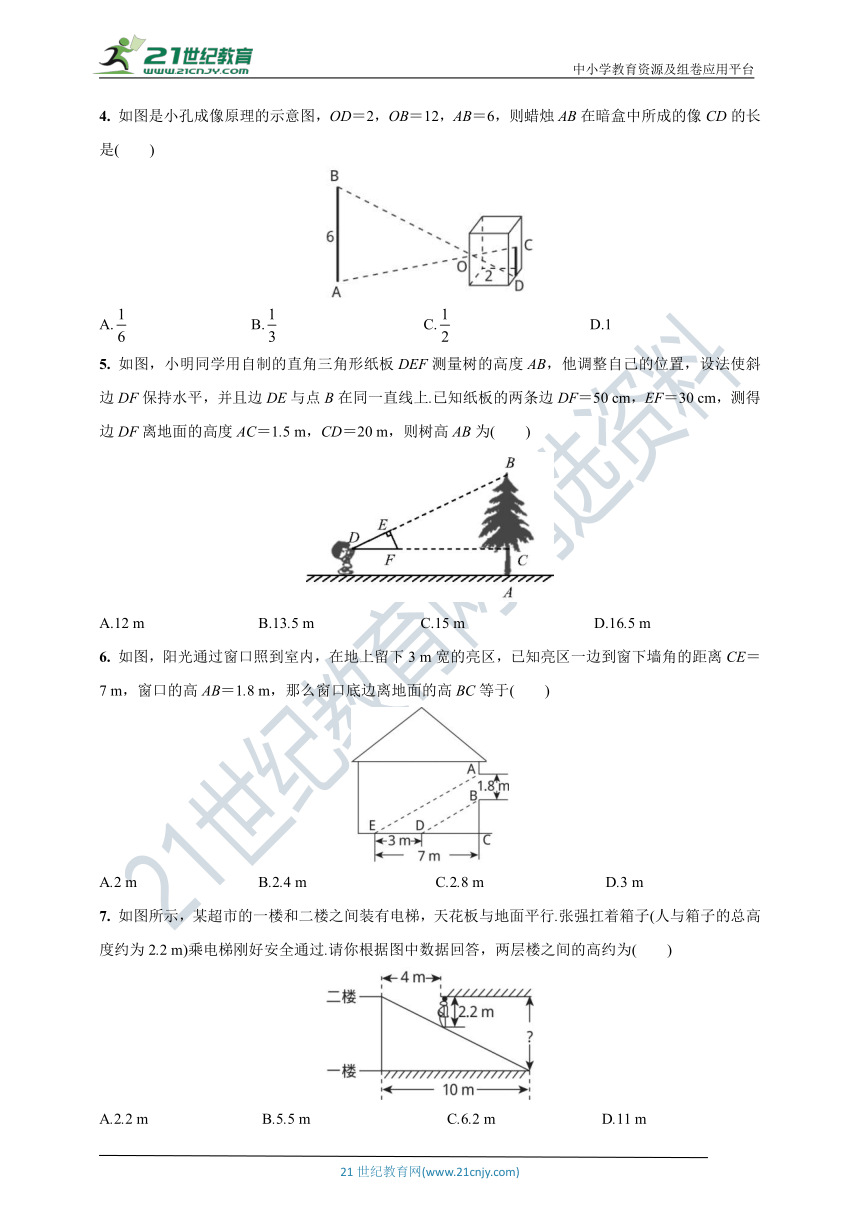
4. 如图是小孔成像原理的示意图,OD=2,OB=12,AB=6,则蜡烛AB在暗盒中所成的像CD的长是( )
A. B. C. D.1
5. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50 cm,EF=30 cm,测得边DF离地面的高度AC=1.5 m,CD=20 m,则树高AB为( )
A.12 m B.13.5 m C.15 m D.16.5 m
6. 如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区,已知亮区一边到窗下墙角的距离CE=7 m,窗口的高AB=1.8 m,那么窗口底边离地面的高BC等于( )
A.2 m B.2.4 m C.2.8 m D.3 m
7. 如图所示,某超市的一楼和二楼之间装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2 m)乘电梯刚好安全通过.请你根据图中数据回答,两层楼之间的高约为( )
A.2.2 m B.5.5 m C.6.2 m D.11 m
8. 如图,已知零件的外径为24 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x= mm.
9. 《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何 ”如图,其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步 ”该问题的答案是 步.
10. 为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B,D,E,C,使点A,B,D在一条直线上,且AD⊥DE,点A,C,E也在一条直线上,且DE∥BC,如图所示.经测量BC=24米,BD=12米,DE=40米,则河的宽度AB为 米.
11. 《孙子算经》中有道歌谣算题:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何
友情提醒:
①歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺.同时立一根一尺五寸的小标杆,它的影长为五寸.请你算一算竹竿的长度是多少.
②丈和尺是古代的长度单位,1丈=10尺,1尺=10寸.
12. 有一块三角形的余料△ABC,它的高AH=40 mm,边BC=80 mm,要把它加工成一个矩形,使矩形的一边EF落在BC上,其余两个顶点D,G分别在AB,AC上,且DG=2DE,求矩形的面积.
13. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30 cm,在其正上方有一个灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为6 cm,那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30 cm的正方形框架按图2摆放,灯泡仍处于两个正方形的正上方.请计算此时横向影子A'B,D'C的长度和为多少
(3)有n个边长为a的正方形按图3摆放,测得横向影子A'B,D'C的长度和为b,灯泡处于n个正方形的正上方.求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
参 考 答 案
1. D 2. A 3. D 4. D 5. D 6. B 7. B
8. 2
9.
10. 18
11. 解:设竹竿的长度为x尺,易得=,解得x=45.答:竹竿的长度是45尺.
12. 解:设AH交DG于点K,设DE=x,则DG=2x. 因为DG∥BC,所以△ADG∽△ABC,所以=,即=,解得x=20,所以2x=40,即DE=20 mm,DG=40 mm,所以矩形EFGD的面积为40×20=800(mm2).
13. 解:(1)180 cm
(2)设横向影子A'B,D'C的长度和为y cm,灯泡的位置为点P. ∵AD∥A'D',∴∠PAD=∠PA'D',∠PDA=∠PD'A',∴△PAD∽△PA'D'. 根据相似三角形对应高的比等于相似比的性质,可得=,∴=,解得y=12. ∴此时横向影子A'B,D'C的长度和为12 cm.
(3)设灯泡离地面的距离为x,记灯泡为点P. 由题意得PM=x,PN=x-a,AD=na,A'D'=na+b,同理可得==1-,=1-,解得x=,
∴灯泡离地面的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十七章 相 似
27.2 相似三角形
27.2.3 相似三角形应用举例
1. 如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5 m,她离镜子的水平距离CE=0.5 m,镜子E离旗杆的底部A处的距离AE=2 m,且A,C,E三点在同一水平直线上,则旗杆AB的高度为( )
A.4.5 m B.4.8 m C.5.5 m D.6 m
2. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处竖立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米 B.12米 C.15米 D.22.5米
3. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是( )
A.24 m B.25 m C.28 m D.30 m
4. 如图是小孔成像原理的示意图,OD=2,OB=12,AB=6,则蜡烛AB在暗盒中所成的像CD的长是( )
A. B. C. D.1
5. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50 cm,EF=30 cm,测得边DF离地面的高度AC=1.5 m,CD=20 m,则树高AB为( )
A.12 m B.13.5 m C.15 m D.16.5 m
6. 如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区,已知亮区一边到窗下墙角的距离CE=7 m,窗口的高AB=1.8 m,那么窗口底边离地面的高BC等于( )
A.2 m B.2.4 m C.2.8 m D.3 m
7. 如图所示,某超市的一楼和二楼之间装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2 m)乘电梯刚好安全通过.请你根据图中数据回答,两层楼之间的高约为( )
A.2.2 m B.5.5 m C.6.2 m D.11 m
8. 如图,已知零件的外径为24 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x= mm.
9. 《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何 ”如图,其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步 ”该问题的答案是 步.
10. 为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B,D,E,C,使点A,B,D在一条直线上,且AD⊥DE,点A,C,E也在一条直线上,且DE∥BC,如图所示.经测量BC=24米,BD=12米,DE=40米,则河的宽度AB为 米.
11. 《孙子算经》中有道歌谣算题:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何
友情提醒:
①歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺.同时立一根一尺五寸的小标杆,它的影长为五寸.请你算一算竹竿的长度是多少.
②丈和尺是古代的长度单位,1丈=10尺,1尺=10寸.
12. 有一块三角形的余料△ABC,它的高AH=40 mm,边BC=80 mm,要把它加工成一个矩形,使矩形的一边EF落在BC上,其余两个顶点D,G分别在AB,AC上,且DG=2DE,求矩形的面积.
13. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30 cm,在其正上方有一个灯泡,在灯泡的照射下,正方形框架的横向影子A'B,D'C的长度和为6 cm,那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30 cm的正方形框架按图2摆放,灯泡仍处于两个正方形的正上方.请计算此时横向影子A'B,D'C的长度和为多少
(3)有n个边长为a的正方形按图3摆放,测得横向影子A'B,D'C的长度和为b,灯泡处于n个正方形的正上方.求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
参 考 答 案
1. D 2. A 3. D 4. D 5. D 6. B 7. B
8. 2
9.
10. 18
11. 解:设竹竿的长度为x尺,易得=,解得x=45.答:竹竿的长度是45尺.
12. 解:设AH交DG于点K,设DE=x,则DG=2x. 因为DG∥BC,所以△ADG∽△ABC,所以=,即=,解得x=20,所以2x=40,即DE=20 mm,DG=40 mm,所以矩形EFGD的面积为40×20=800(mm2).
13. 解:(1)180 cm
(2)设横向影子A'B,D'C的长度和为y cm,灯泡的位置为点P. ∵AD∥A'D',∴∠PAD=∠PA'D',∠PDA=∠PD'A',∴△PAD∽△PA'D'. 根据相似三角形对应高的比等于相似比的性质,可得=,∴=,解得y=12. ∴此时横向影子A'B,D'C的长度和为12 cm.
(3)设灯泡离地面的距离为x,记灯泡为点P. 由题意得PM=x,PN=x-a,AD=na,A'D'=na+b,同理可得==1-,=1-,解得x=,
∴灯泡离地面的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
