(新人教版)八年级数学上册课件15.1.1同底数幂乘法
文档属性
| 名称 | (新人教版)八年级数学上册课件15.1.1同底数幂乘法 |

|
|
| 格式 | zip | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-24 23:13:36 | ||
图片预览


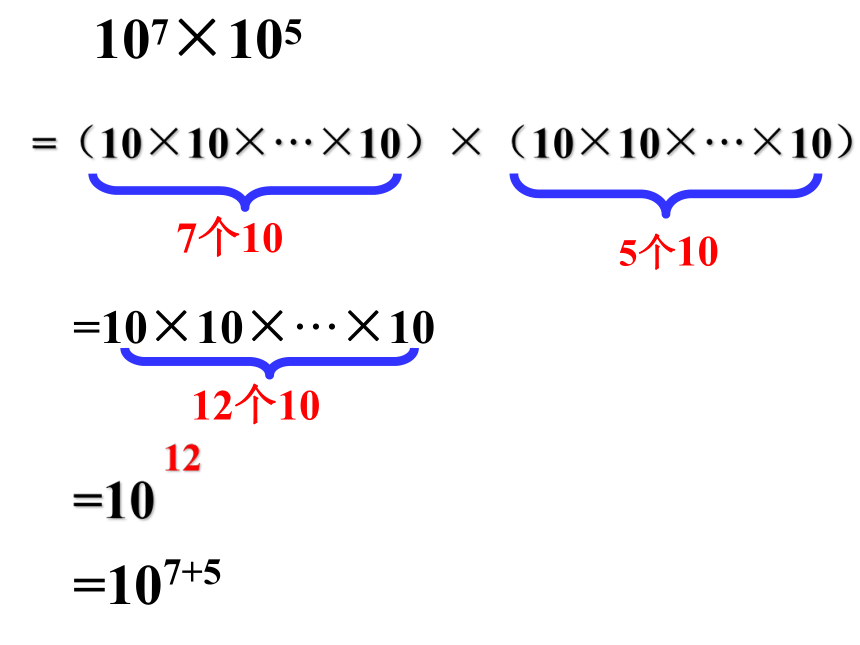




文档简介
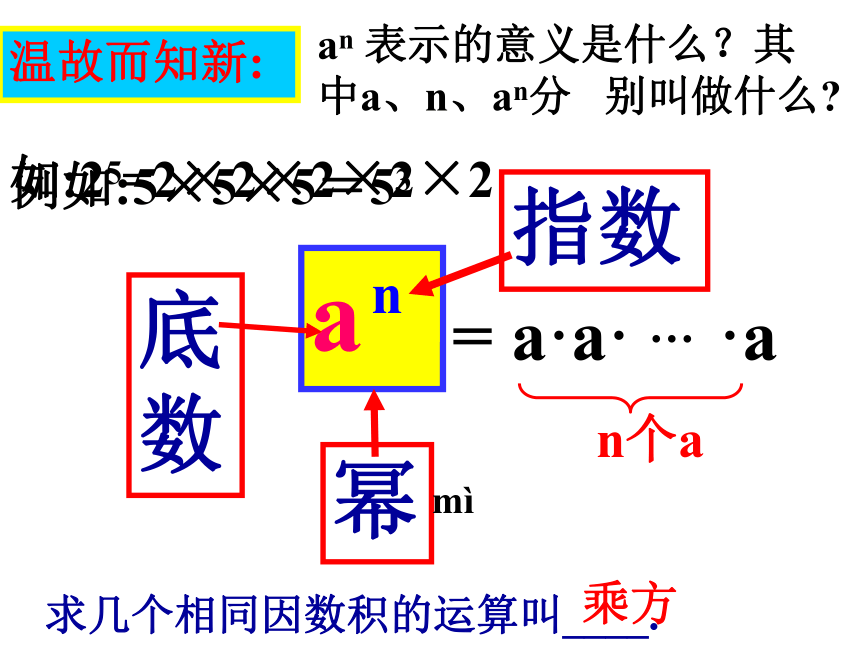
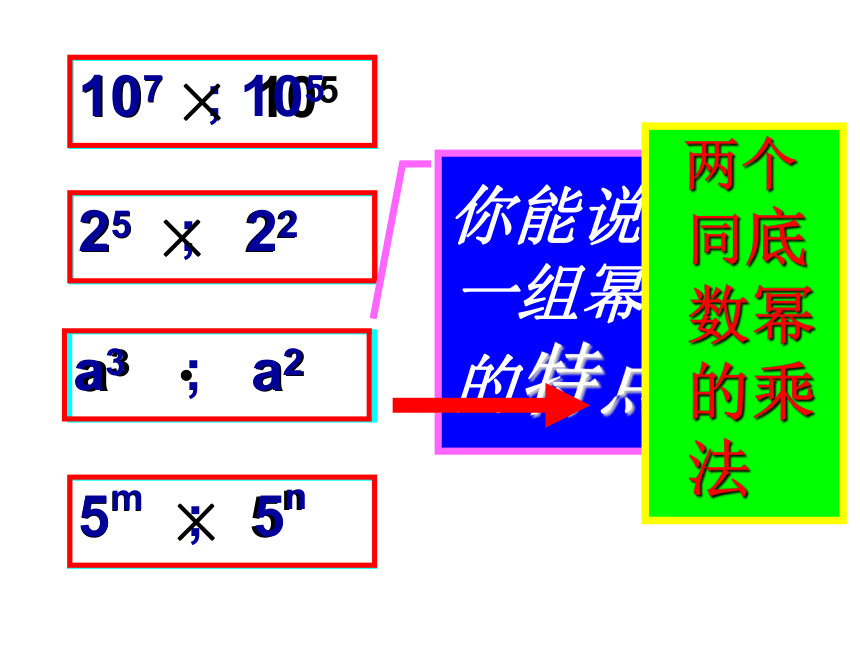
课件23张PPT。15.1.1同底数幂的乘法23×26103×102?温故而知新:指数幂= a·a· … ·a如:25=2×2×2×2×2例如:5×5×5=53an 表示的意义是什么?其中a、n、an分 别叫做什么? mì求几个相同因数积的运算叫____.乘方(2)10×10×10×10可以写成____;(3) a的底数是__,指数是__;2×2×2×2×2a1a+b3-2424回眸 · 热身107 10525 22a3 a25m 5n 你能说出每一组幂具备的特点吗?=(10×10×···×10)×(10×10×···×10)5个10107×105=107+5
25 × 22 a3 · a25m × 5n聪明的你来做一做=25+2=a3+2=5m+n你发现了什么? am · an=am+n两个同底数幂相乘,底数不变, 指数相加. am · an · ap三个同底数幂相乘
底数 ,
指数 .不变相加=am+n+pam · an =am+n
(m,n都是正整数) 同底数幂相乘,底数不变, 指数相加.请你一定要记住哟!例1计算:⑴⑵⑶⑵⑶理解法则www.czsx.com.cn填空:
(1)x5 ·( )=x 8 (2)a ·( )= a6
(3)x · x3( )= x7(4)xm ·( )=x3m
逆向训练x3a5 x3x2mam· an =a m+n 同底数幂相乘,底数不变,指数相加.am+n =am· an 指数为和的幂等于以和中每个加数为指数的同底数幂的积. (x+y)3 · (x+y)4 .解:(x+y)3 · (x+y)4am · an = am+n 公式中的a可代表单项式,也可以代表多项式.=(x+y)3+4 =(x+y)7想一想例2计算:例3.计算: (1) - a2 · a6 ;解:(2)(-x)· (-x)3原式 = (-x)1+3= (-x)4=-a8= x4原式 = -a2+ 6解:计算
(-2)3×(-2)5
(2) (-2)2×(-2)7
(3) (-2)3×25
(4) (-2)2×27 ( 28 )
(-29 )
(- 28 )
( 29 )看谁说得快:偶去奇提· (y-x)3 (x-y)2· (n-m)6 (m-n)5例3 光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?解: 3×105×5×102=15×107=1.5×108(千米)地球距离太阳大约有1.5×108千米.=1.5×10×107本节课你感悟到了什么?课堂小结am · an =am+n(m,n都是正整数)同底数幂的乘法性质:底数 ,指数 .不变相加am · an · ap =am+n+p(m,n,p都是正整数)练习
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( )
b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ××我是法官我来判 填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×= 1.已知:a5=7;a3=16.则a8=( ) 2.已知2m=a,2n=b,(m,n都是正整数).则2m+n=( ) 3.计算: (-2)2006 - 22007112ab=22006 – (2×22006) =22006(1-2) =22006(-1) =-22006 逆向转换a8=a5+3=a5· a3=7×16数学沙龙,智慧无限.
(1)计算: x · x2 · x3 · x4 · ··· ·x100
(2)已知: 2×8n×16n=222,求n的值
(3)如果 x m-n · x 2n+1=x 11 , 且y m-1 · y 4-n = y 7 ,
求m , n的值
25 × 22 a3 · a25m × 5n聪明的你来做一做=25+2=a3+2=5m+n你发现了什么? am · an=am+n两个同底数幂相乘,底数不变, 指数相加. am · an · ap三个同底数幂相乘
底数 ,
指数 .不变相加=am+n+pam · an =am+n
(m,n都是正整数) 同底数幂相乘,底数不变, 指数相加.请你一定要记住哟!例1计算:⑴⑵⑶⑵⑶理解法则www.czsx.com.cn填空:
(1)x5 ·( )=x 8 (2)a ·( )= a6
(3)x · x3( )= x7(4)xm ·( )=x3m
逆向训练x3a5 x3x2mam· an =a m+n 同底数幂相乘,底数不变,指数相加.am+n =am· an 指数为和的幂等于以和中每个加数为指数的同底数幂的积. (x+y)3 · (x+y)4 .解:(x+y)3 · (x+y)4am · an = am+n 公式中的a可代表单项式,也可以代表多项式.=(x+y)3+4 =(x+y)7想一想例2计算:例3.计算: (1) - a2 · a6 ;解:(2)(-x)· (-x)3原式 = (-x)1+3= (-x)4=-a8= x4原式 = -a2+ 6解:计算
(-2)3×(-2)5
(2) (-2)2×(-2)7
(3) (-2)3×25
(4) (-2)2×27 ( 28 )
(-29 )
(- 28 )
( 29 )看谁说得快:偶去奇提· (y-x)3 (x-y)2· (n-m)6 (m-n)5例3 光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?解: 3×105×5×102=15×107=1.5×108(千米)地球距离太阳大约有1.5×108千米.=1.5×10×107本节课你感悟到了什么?课堂小结am · an =am+n(m,n都是正整数)同底数幂的乘法性质:底数 ,指数 .不变相加am · an · ap =am+n+p(m,n,p都是正整数)练习
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( )
b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ××我是法官我来判 填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×= 1.已知:a5=7;a3=16.则a8=( ) 2.已知2m=a,2n=b,(m,n都是正整数).则2m+n=( ) 3.计算: (-2)2006 - 22007112ab=22006 – (2×22006) =22006(1-2) =22006(-1) =-22006 逆向转换a8=a5+3=a5· a3=7×16数学沙龙,智慧无限.
(1)计算: x · x2 · x3 · x4 · ··· ·x100
(2)已知: 2×8n×16n=222,求n的值
(3)如果 x m-n · x 2n+1=x 11 , 且y m-1 · y 4-n = y 7 ,
求m , n的值
