(华师大版)七年级数学上册课件 有理数的乘方
文档属性
| 名称 | (华师大版)七年级数学上册课件 有理数的乘方 |  | |
| 格式 | zip | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-19 22:25:50 | ||
图片预览




文档简介
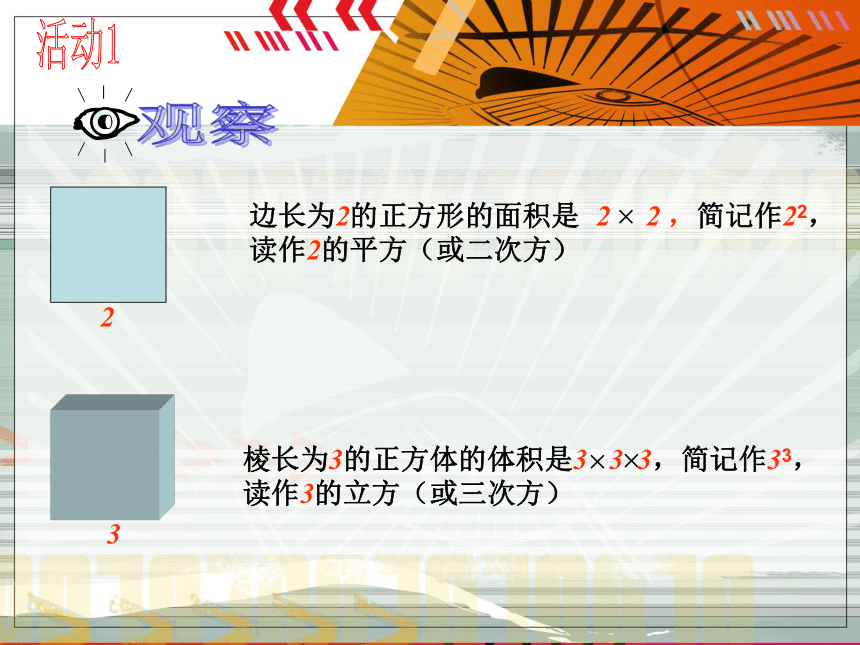
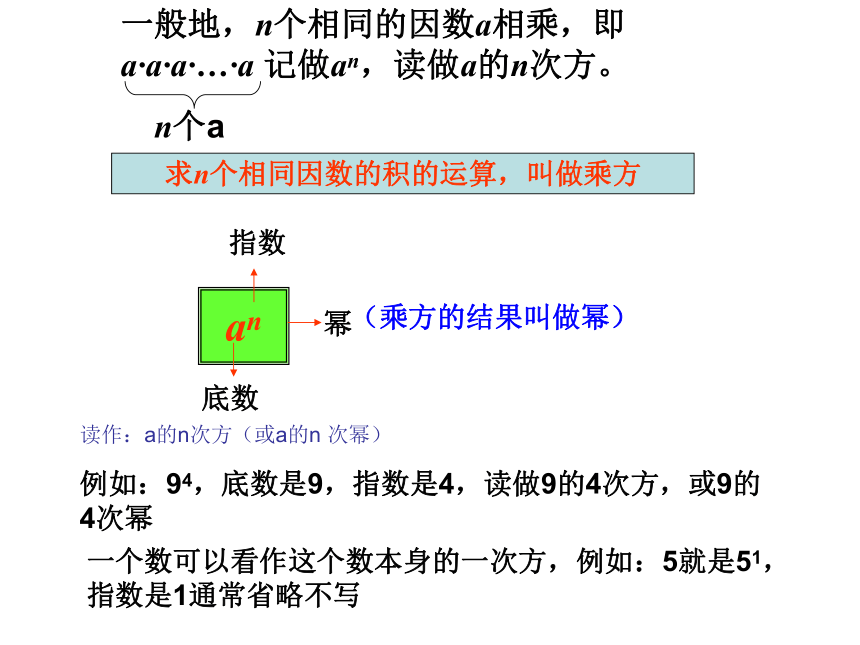
课件17张PPT。第一章 有理数 1.5.1 乘方(第1课时)2边长为2的正方形的面积是 2 2 ,简记作22,读作2的平方(或二次方)棱长为3的正方体的体积是3 3 3,简记作33,读作3的立方(或三次方)3活动12个 相加可记为:3个 相加可为:4个 相加可为: 个 相加可记为:边长为 的正方形的面积可记为:那么4个 相乘可记为:棱长为 的正方体的体积可记为:个 相乘又可记为:求n个相同因数的积的运算,叫做乘方an底数幂指数(乘方的结果叫做幂)读作:a的n次方(或a的n 次幂)
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂一个数可以看作这个数本身的一次方,例如:5就是51,指数是1通常省略不写口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7的7次方底指12的10次方 3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;底指-3的16次方17 的17次方
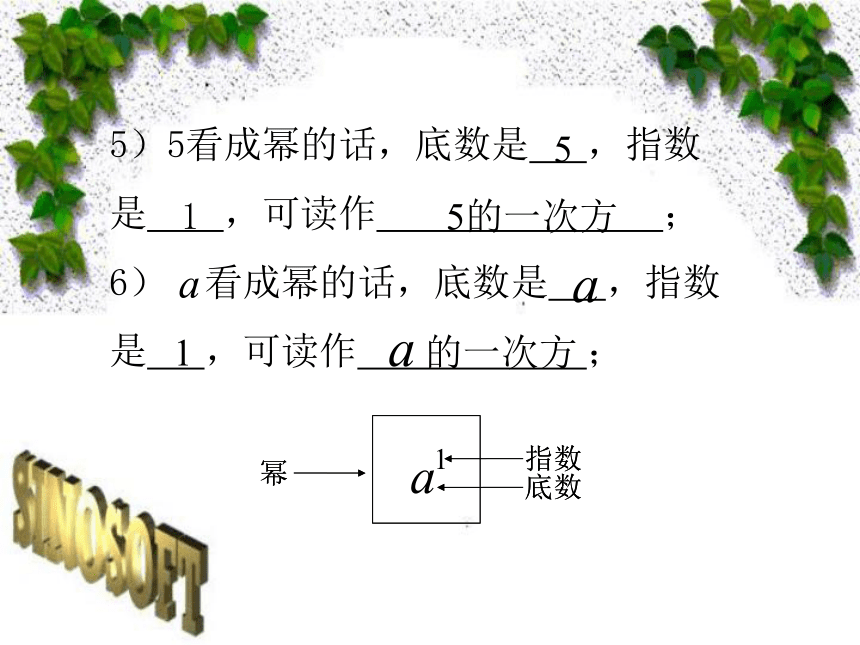
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ; 幂指数底数515的一次方1的一次方
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ 对错错错解:(1)=(-4)×(-4)×(-4)=(2)=(-2)×(-2)×(-2)X(-2)=活动2因为 就是n个a相乘,所以可以利用有理数的乘法运算来进行有理数的乘方运算-6416从例1和例2,你发现负数的幂的正负有什么规律?
当指数是( )数时,负数的幂是( )
当指数是( )数时,负数的幂( ) 观察与思考奇负偶正根据有理数的乘法法则可以得出
负数的奇次幂是负数,负数的偶次幂是正数
显然,正数的任何次幂都是正数,0的任何正整数次幂都是0显示:-32768显示: 729(-10)4(-10)5活动3练习
1、计算
(1) (2) (3) (4)
(5) (6) (7) (8)(-1)7(-1)10(-5)3 (- )4(-10)4(-10)5解:=1=-1=512=-125=0.001=10000=-1000002、用计算器计算(-11)61678.43(-5.6)3小结1、乘方的概念:求n个相同因数的积的运算叫做乘方2、乘方负号的确定an底数幂(乘方的结果叫做幂)指数an读法:a的n次方或a的n次幂 负数的积次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0活动4
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂一个数可以看作这个数本身的一次方,例如:5就是51,指数是1通常省略不写口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7的7次方底指12的10次方 3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;底指-3的16次方17 的17次方
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ; 幂指数底数515的一次方1的一次方
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ 对错错错解:(1)=(-4)×(-4)×(-4)=(2)=(-2)×(-2)×(-2)X(-2)=活动2因为 就是n个a相乘,所以可以利用有理数的乘法运算来进行有理数的乘方运算-6416从例1和例2,你发现负数的幂的正负有什么规律?
当指数是( )数时,负数的幂是( )
当指数是( )数时,负数的幂( ) 观察与思考奇负偶正根据有理数的乘法法则可以得出
负数的奇次幂是负数,负数的偶次幂是正数
显然,正数的任何次幂都是正数,0的任何正整数次幂都是0显示:-32768显示: 729(-10)4(-10)5活动3练习
1、计算
(1) (2) (3) (4)
(5) (6) (7) (8)(-1)7(-1)10(-5)3 (- )4(-10)4(-10)5解:=1=-1=512=-125=0.001=10000=-1000002、用计算器计算(-11)61678.43(-5.6)3小结1、乘方的概念:求n个相同因数的积的运算叫做乘方2、乘方负号的确定an底数幂(乘方的结果叫做幂)指数an读法:a的n次方或a的n次幂 负数的积次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0活动4
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
