1.5弹性碰撞和非弹性碰撞课件(共31张PPT)
文档属性
| 名称 | 1.5弹性碰撞和非弹性碰撞课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-06 15:57:12 | ||
图片预览






文档简介
(共31张PPT)
第5节 弹性碰撞与非弹性碰撞
新人教版 选择性必修一
第一章 动量守恒定律
问题引入:
碰撞是自然界中常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……物体碰撞中动量的变化情况,前面已进行了研究。
思考:碰撞中动量为什么是守恒的?
1.碰撞时间短,内力远远大于外力.
碰撞过程中动量守恒,动能守恒吗?
碰撞过程中没有宏观位移,但每个物体在短时间内运动状态显著变化.
3.
2.碰撞过程中相互作用力大,.
A
B
mA=0.3kg,mB=0.1kg,vA=8m/s,vB=0
2、若碰后v'A=5m/s,v'B=9m/s,请计算碰撞前后动能变化
3、若碰后AB连在一起v=6m/s,请计算碰撞前后动能变化
动能减少1.8J
动能减少2.4J
1、若碰后v'A=4m/s,v'B=12m/s,请计算碰撞前后动能变化
碰撞前:
碰撞后:
动能不变
碰撞前:
碰撞后:
碰撞前:
碰撞后:
弹性碰撞:碰撞后物体的形变可以完全恢复,且碰
撞前后系统的总机械能不损失E1=E2.
非弹性碰撞:碰撞后物体的形变只有部分恢复,
系统有部分机械能损失E1>E2.
完全非弹性碰撞:碰撞过程中物体的形变完全不能恢复,以致物体合为一体一起运动,即两物体在非弹性碰撞后以同一速度运动,系统损失的机械能最大.
碰撞分类
例:微观世界粒子的碰撞即为弹性碰撞
两个物体碰撞后成为一个整体,以共同的速度运动,即为完全非弹性碰撞,损失动能最大
例:
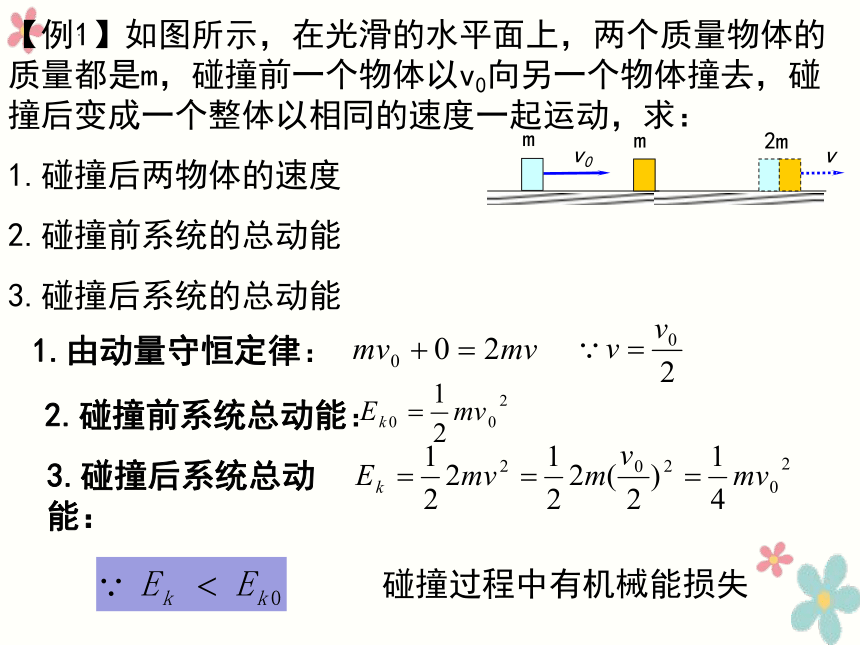
1.由动量守恒定律:
2.碰撞前系统总动能:
3.碰撞后系统总动能:
碰撞过程中有机械能损失
【例1】如图所示,在光滑的水平面上,两个质量物体的质量都是m,碰撞前一个物体以v0向另一个物体撞去,碰撞后变成一个整体以相同的速度一起运动,求:
1.碰撞后两物体的速度
2.碰撞前系统的总动能
3.碰撞后系统的总动能
v
v0
m
2m
m
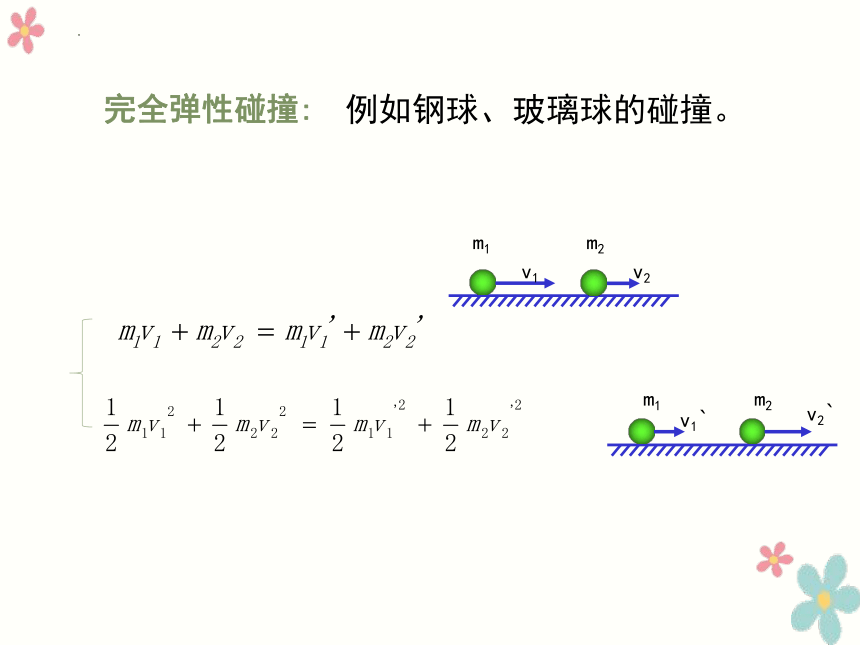
完全弹性碰撞:
m1
m2
m1
m2
v1`
v2`
v1
v2
例如钢球、玻璃球的碰撞。
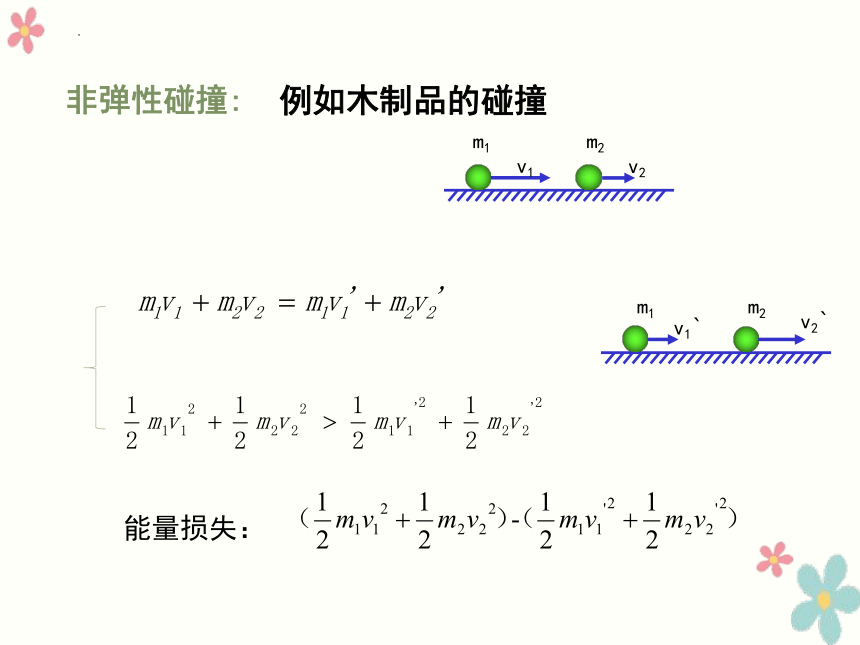
非弹性碰撞:
m1
m2
m1
m2
v1`
v2`
v1
v2
例如木制品的碰撞
能量损失:
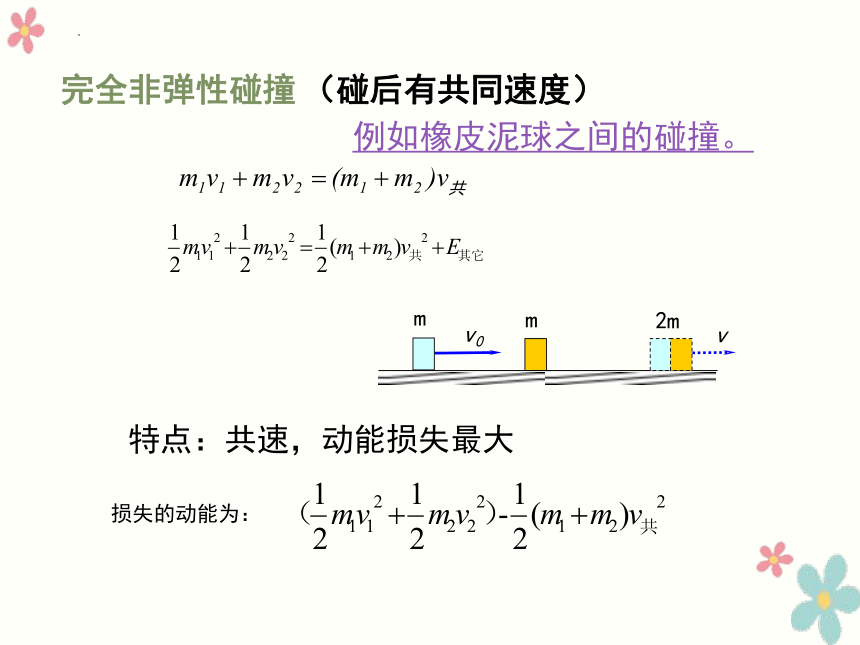
完全非弹性碰撞
(碰后有共同速度)
特点:共速,动能损失最大
v
v0
m
2m
m
损失的动能为:
例如橡皮泥球之间的碰撞。
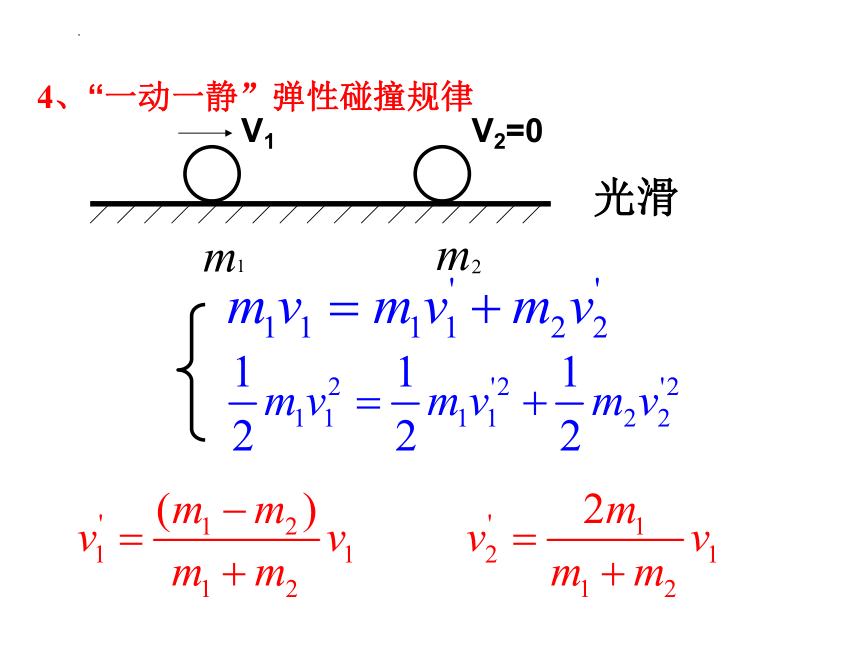
V1
V2=0
光滑
4、“一动一静”弹性碰撞规律
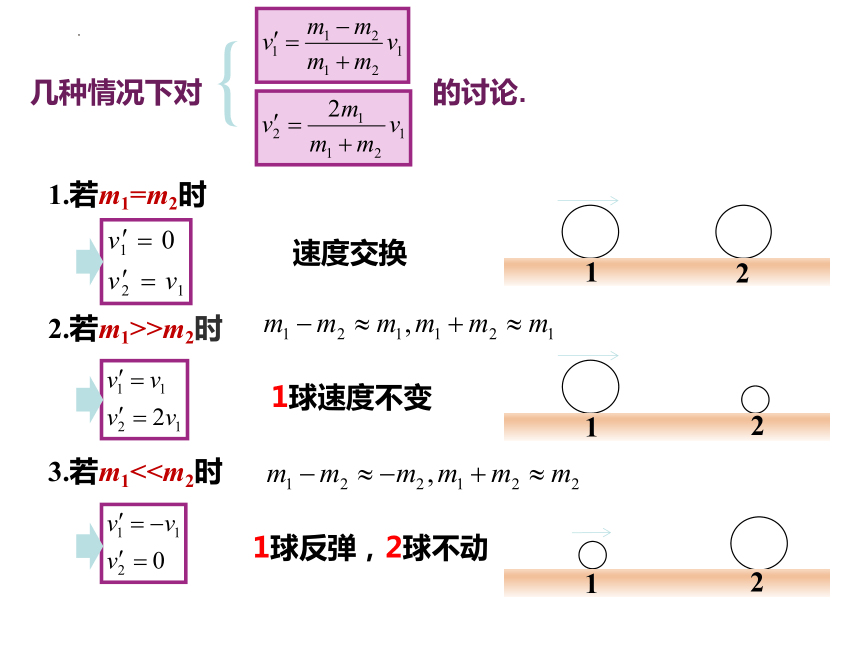
几种情况下对 的讨论.
1.若m1=m2时
2.若m1>>m2时
2
1
2
1
2
1
3.若m1<速度交换
1球反弹,2球不动
1球速度不变
例1.冰球运动员甲的质量为80.0kg。当他以5.0 m/s的速度向前运动时,与另一质量为100 kg、速度为3.0 m/s的迎面而来的运动员乙相撞。碰撞后甲恰好静止。假设碰撞时间极短,求:
(1)碰撞后乙的速度的大小;
(2)碰撞中总机械能的损失。
1.0 m/s
1400J
属于非弹性碰撞和完全非弹性碰撞
思考:如果碰撞后两球粘连在一起,则各球速度又是多少?动能的损失又是多少?一,两次分别属于什么碰撞?
二 按碰撞前后轨迹分类
1.对心碰撞:碰撞前后速度都沿同一条直线
2.非对心碰撞:碰撞前后速度不沿同一条直线
v'1
m1
m2
v'2
v1
m1
m2
v1
m1
m2
v'1
m1
m2
v'2
例:α粒子散射
由于微观粒子与物质微粒的碰撞并非直接接触,而是相互靠近,且发生对心碰撞的几率很小,所以大多数粒子在碰撞后飞向四面八方,这就是散射。
金原子对α粒子的散射
光滑水平面上的两个物体发生碰撞,下列情形可能成立的是 ( )
A.碰撞后系统的总动能比碰撞前小,但系统的总动量守恒
B.碰撞前后系统的总动量不守恒,但系统的总动能守恒
C.碰撞后系统的总动能比碰撞前大,但系统的总动量守恒
D.碰撞前后系统的总动量、总动能均守恒
AD
(北京理综)(1)如图甲所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为m1的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为m2的小球发生碰撞,碰撞前后两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失,求碰撞后小球m2的速度大小v2。
课堂小结
一 按碰撞前后能量变化分类
二 按碰撞前后轨迹分类
1.弹性碰撞
2.非弹性碰撞
3.完全非弹性碰撞
1.对心碰撞
2.非对心碰撞:散射
题型一.碰撞可能性判断的三个依据:
——守恒
——不增
——合理
分析碰撞问题时的关键点
(1)遵守动量守恒定律。
(2)系统的动能应不增加。
(3)碰撞后各物体的运动情况要符合实际情况。
动量制约
动能制约
运动制约
如果碰前是同向运动,碰前v后> v前;碰后前面物体速度一定增加,若运动同向
如果碰前是相向运动,两物体的运动方向不可能都不改变,除非都变为0
例5.两球A、B在光滑水平面上沿同一直线、同一方向运动,mA=1 kg,mB=2 kg,vA=6 m/s,vB=2 m/s,当球A追上B并发生碰撞后,两球A、B速度的可能值是(取两球碰撞前的运动方向为正)( )
A.vA′=5 m/s,vB′=2.5 m/s
B.vA′=2 m/s,vB′=4 m/s
C.vA′=-4 m/s,vB′=7 m/s
D.vA′=7 m/s,vB′= 1.5 m/s
P=mAvA+mBvB=10kg.m/s
///////////////////////
A
B
解析
1.碰撞前后动量守恒
碰撞后
PA’ =PB’ =PC’ =PD’ =10kg.m/s
碰撞前
2.如碰撞后向同方向运动,则后面物体的速度不能大于前面物体的速度.
排除AD
即碰撞后:A的速度减小,或反向,
B的速度增大
3.系统的总动能不能增加
排除C
B
题型二.碰撞中的弹簧模型
1.弹簧处于最长(最短)状态时,两物体速度相等,弹性势能最大:
①动量守恒:
②最大弹性势能:
2.弹簧处于原长时,弹性势能为零,动能守恒:
①动量守恒:
②动能守恒:
本题涉及完全非弹性碰撞模型和弹簧模型,涉及弹性势能的变化的计算,而过程也多达3个阶段。对于这种多过程复杂问题,要有清晰的思路,应该分阶段画好过程草图,并弄清楚不同阶段相互作用的物体是哪几个,从而才可能正确选取研究对象和确定研究对象的初末状态,进而正确列出方程求解。
按照事物发展的先后顺序,一步一步地画好过程草图如图乙所示,然后再答题。过程如下:
①→②:A、B相互作用,压缩弹簧,达到共同速度v1。
②→③:B、C完全非弹性碰撞,结为一体,具有共同速度v2(v2③→④:A向右继续压缩弹簧,A减速,B、C加速,直到三者达到共同速度v3(v3>v2)。
M
m
v0
x
S
f
f
v
结论:系统动量守恒
题型三.板块模型
1.在气垫导轨上,一个质量为600g的滑块以15cm/s的速度与另一个质量为400g,速度为10cm/s并沿反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起,求碰撞后滑块速度的大小和方向.
解:以600g的滑块的初速度方向为正方向,根据动量守恒定律
与初速度方向相同
2.质量为m、速度为v的A球跟质量为3m的静止B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度可能有不同的值.请你论证:碰后B球的速度可能是以下值吗?
(1)0.6v;(2)0.4v;(3)0.2v
若A、B弹性碰撞,根据动量守恒定律和机械能守恒定律得B获得的最大速度为
解:
若A、B完全非弹性碰撞,根据动量守恒定律,B获得的最小速度为
3.速度为103m/s的氦核与静止的质子发生正碰,氦核的质量是质子的4倍,碰撞时弹性的,求碰撞后两个粒子的速度.
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
氦核:
质子:
4.有些核反应堆里要让中子与原子核正碰,以便把中子的速率降下来.为此应该选用质量较大的还是质量较小的原子核?为什么?
解:中子和原子核的碰撞可看做是弹性碰撞,设
中子:质量m1,碰前v,方向为正,碰后速度v
原子核:质量m2,碰前静止
中子质量一般小于原子核的质量,因此
m2越小,v 越小,故选择质量较小的原子核来降低中子的速度。核电站常用石墨作为中子减速剂。
5.一种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度是3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.7×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.中子的质量与氢原子核的质量mH有什么关系.
查德威克发现中子实验
碰后氮原子核的速度为
设未知粒子质量m,速度v。它与氢和氮原子核碰撞都是弹性的,碰后氢原子核的速度为
解:
两式联立,解得未知粒子的质量为1.16mH
v0
m
M
例2、如图所示,一质量为m的子弹以水平速度 v0飞向小球,小球的质量为M,悬挂小球的绳长为 ,子弹击中小球并留在其中,求(1)子弹打小球过程中所产生的热量(2)小球向右摆起的最大高度(已知高度小于 )。
第5节 弹性碰撞与非弹性碰撞
新人教版 选择性必修一
第一章 动量守恒定律
问题引入:
碰撞是自然界中常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……物体碰撞中动量的变化情况,前面已进行了研究。
思考:碰撞中动量为什么是守恒的?
1.碰撞时间短,内力远远大于外力.
碰撞过程中动量守恒,动能守恒吗?
碰撞过程中没有宏观位移,但每个物体在短时间内运动状态显著变化.
3.
2.碰撞过程中相互作用力大,.
A
B
mA=0.3kg,mB=0.1kg,vA=8m/s,vB=0
2、若碰后v'A=5m/s,v'B=9m/s,请计算碰撞前后动能变化
3、若碰后AB连在一起v=6m/s,请计算碰撞前后动能变化
动能减少1.8J
动能减少2.4J
1、若碰后v'A=4m/s,v'B=12m/s,请计算碰撞前后动能变化
碰撞前:
碰撞后:
动能不变
碰撞前:
碰撞后:
碰撞前:
碰撞后:
弹性碰撞:碰撞后物体的形变可以完全恢复,且碰
撞前后系统的总机械能不损失E1=E2.
非弹性碰撞:碰撞后物体的形变只有部分恢复,
系统有部分机械能损失E1>E2.
完全非弹性碰撞:碰撞过程中物体的形变完全不能恢复,以致物体合为一体一起运动,即两物体在非弹性碰撞后以同一速度运动,系统损失的机械能最大.
碰撞分类
例:微观世界粒子的碰撞即为弹性碰撞
两个物体碰撞后成为一个整体,以共同的速度运动,即为完全非弹性碰撞,损失动能最大
例:
1.由动量守恒定律:
2.碰撞前系统总动能:
3.碰撞后系统总动能:
碰撞过程中有机械能损失
【例1】如图所示,在光滑的水平面上,两个质量物体的质量都是m,碰撞前一个物体以v0向另一个物体撞去,碰撞后变成一个整体以相同的速度一起运动,求:
1.碰撞后两物体的速度
2.碰撞前系统的总动能
3.碰撞后系统的总动能
v
v0
m
2m
m
完全弹性碰撞:
m1
m2
m1
m2
v1`
v2`
v1
v2
例如钢球、玻璃球的碰撞。
非弹性碰撞:
m1
m2
m1
m2
v1`
v2`
v1
v2
例如木制品的碰撞
能量损失:
完全非弹性碰撞
(碰后有共同速度)
特点:共速,动能损失最大
v
v0
m
2m
m
损失的动能为:
例如橡皮泥球之间的碰撞。
V1
V2=0
光滑
4、“一动一静”弹性碰撞规律
几种情况下对 的讨论.
1.若m1=m2时
2.若m1>>m2时
2
1
2
1
2
1
3.若m1<
1球反弹,2球不动
1球速度不变
例1.冰球运动员甲的质量为80.0kg。当他以5.0 m/s的速度向前运动时,与另一质量为100 kg、速度为3.0 m/s的迎面而来的运动员乙相撞。碰撞后甲恰好静止。假设碰撞时间极短,求:
(1)碰撞后乙的速度的大小;
(2)碰撞中总机械能的损失。
1.0 m/s
1400J
属于非弹性碰撞和完全非弹性碰撞
思考:如果碰撞后两球粘连在一起,则各球速度又是多少?动能的损失又是多少?一,两次分别属于什么碰撞?
二 按碰撞前后轨迹分类
1.对心碰撞:碰撞前后速度都沿同一条直线
2.非对心碰撞:碰撞前后速度不沿同一条直线
v'1
m1
m2
v'2
v1
m1
m2
v1
m1
m2
v'1
m1
m2
v'2
例:α粒子散射
由于微观粒子与物质微粒的碰撞并非直接接触,而是相互靠近,且发生对心碰撞的几率很小,所以大多数粒子在碰撞后飞向四面八方,这就是散射。
金原子对α粒子的散射
光滑水平面上的两个物体发生碰撞,下列情形可能成立的是 ( )
A.碰撞后系统的总动能比碰撞前小,但系统的总动量守恒
B.碰撞前后系统的总动量不守恒,但系统的总动能守恒
C.碰撞后系统的总动能比碰撞前大,但系统的总动量守恒
D.碰撞前后系统的总动量、总动能均守恒
AD
(北京理综)(1)如图甲所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为m1的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为m2的小球发生碰撞,碰撞前后两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失,求碰撞后小球m2的速度大小v2。
课堂小结
一 按碰撞前后能量变化分类
二 按碰撞前后轨迹分类
1.弹性碰撞
2.非弹性碰撞
3.完全非弹性碰撞
1.对心碰撞
2.非对心碰撞:散射
题型一.碰撞可能性判断的三个依据:
——守恒
——不增
——合理
分析碰撞问题时的关键点
(1)遵守动量守恒定律。
(2)系统的动能应不增加。
(3)碰撞后各物体的运动情况要符合实际情况。
动量制约
动能制约
运动制约
如果碰前是同向运动,碰前v后> v前;碰后前面物体速度一定增加,若运动同向
如果碰前是相向运动,两物体的运动方向不可能都不改变,除非都变为0
例5.两球A、B在光滑水平面上沿同一直线、同一方向运动,mA=1 kg,mB=2 kg,vA=6 m/s,vB=2 m/s,当球A追上B并发生碰撞后,两球A、B速度的可能值是(取两球碰撞前的运动方向为正)( )
A.vA′=5 m/s,vB′=2.5 m/s
B.vA′=2 m/s,vB′=4 m/s
C.vA′=-4 m/s,vB′=7 m/s
D.vA′=7 m/s,vB′= 1.5 m/s
P=mAvA+mBvB=10kg.m/s
///////////////////////
A
B
解析
1.碰撞前后动量守恒
碰撞后
PA’ =PB’ =PC’ =PD’ =10kg.m/s
碰撞前
2.如碰撞后向同方向运动,则后面物体的速度不能大于前面物体的速度.
排除AD
即碰撞后:A的速度减小,或反向,
B的速度增大
3.系统的总动能不能增加
排除C
B
题型二.碰撞中的弹簧模型
1.弹簧处于最长(最短)状态时,两物体速度相等,弹性势能最大:
①动量守恒:
②最大弹性势能:
2.弹簧处于原长时,弹性势能为零,动能守恒:
①动量守恒:
②动能守恒:
本题涉及完全非弹性碰撞模型和弹簧模型,涉及弹性势能的变化的计算,而过程也多达3个阶段。对于这种多过程复杂问题,要有清晰的思路,应该分阶段画好过程草图,并弄清楚不同阶段相互作用的物体是哪几个,从而才可能正确选取研究对象和确定研究对象的初末状态,进而正确列出方程求解。
按照事物发展的先后顺序,一步一步地画好过程草图如图乙所示,然后再答题。过程如下:
①→②:A、B相互作用,压缩弹簧,达到共同速度v1。
②→③:B、C完全非弹性碰撞,结为一体,具有共同速度v2(v2
M
m
v0
x
S
f
f
v
结论:系统动量守恒
题型三.板块模型
1.在气垫导轨上,一个质量为600g的滑块以15cm/s的速度与另一个质量为400g,速度为10cm/s并沿反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起,求碰撞后滑块速度的大小和方向.
解:以600g的滑块的初速度方向为正方向,根据动量守恒定律
与初速度方向相同
2.质量为m、速度为v的A球跟质量为3m的静止B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度可能有不同的值.请你论证:碰后B球的速度可能是以下值吗?
(1)0.6v;(2)0.4v;(3)0.2v
若A、B弹性碰撞,根据动量守恒定律和机械能守恒定律得B获得的最大速度为
解:
若A、B完全非弹性碰撞,根据动量守恒定律,B获得的最小速度为
3.速度为103m/s的氦核与静止的质子发生正碰,氦核的质量是质子的4倍,碰撞时弹性的,求碰撞后两个粒子的速度.
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
氦核:
质子:
4.有些核反应堆里要让中子与原子核正碰,以便把中子的速率降下来.为此应该选用质量较大的还是质量较小的原子核?为什么?
解:中子和原子核的碰撞可看做是弹性碰撞,设
中子:质量m1,碰前v,方向为正,碰后速度v
原子核:质量m2,碰前静止
中子质量一般小于原子核的质量,因此
m2越小,v 越小,故选择质量较小的原子核来降低中子的速度。核电站常用石墨作为中子减速剂。
5.一种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度是3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.7×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.中子的质量与氢原子核的质量mH有什么关系.
查德威克发现中子实验
碰后氮原子核的速度为
设未知粒子质量m,速度v。它与氢和氮原子核碰撞都是弹性的,碰后氢原子核的速度为
解:
两式联立,解得未知粒子的质量为1.16mH
v0
m
M
例2、如图所示,一质量为m的子弹以水平速度 v0飞向小球,小球的质量为M,悬挂小球的绳长为 ,子弹击中小球并留在其中,求(1)子弹打小球过程中所产生的热量(2)小球向右摆起的最大高度(已知高度小于 )。
