6.4生活中的圆周运动课件(共28张PPT)
文档属性
| 名称 | 6.4生活中的圆周运动课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-06 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第四节 生活中的圆周运动
学习目标:
1.定性分析生活中圆周运动的向心力的来源
2.能分析火车转弯、汽车过拱、凹型桥的压力问题
3.能用牛顿第二定律分析圆周运动
4.知道航天器中的失重现象的本质,知道离心运动及其产生的条件
5.领会力与物体的惯性对运动状态变化所起的作用
火车车轮有突出的轮缘
火车、汽车拐弯
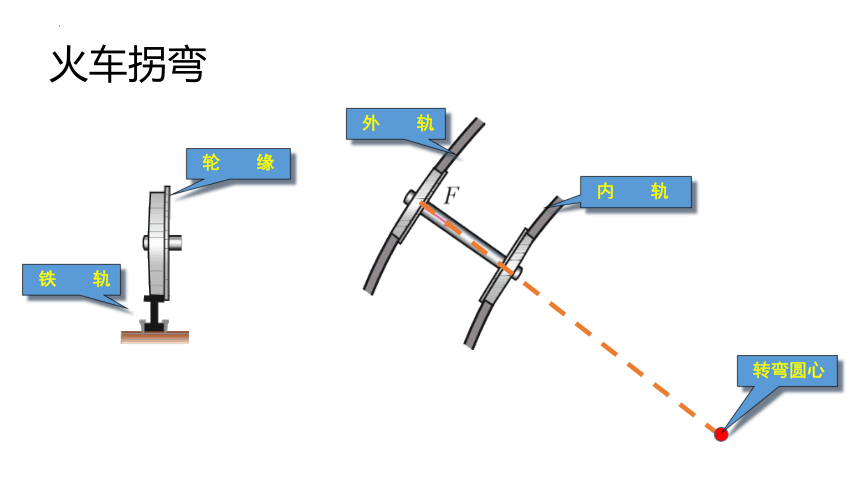
火车拐弯
若铁道的内外轨一样高,火车在转弯时,谁提供向心力?这个力需要多大?(已知:火车速度v为30m/s,弯道的半径R=900m,火车的质量m=8×105kg)
危害?
如何避免?
火车拐弯
铁 轨
轮 缘
外 轨
内 轨
转弯圆心
火车拐弯
若火车转弯时轨道倾角为5 ,此时要求轨道对轮缘无挤压作用,请问火车通过弯道时的最大速度是多少?(已知:转弯半径R=900m,tan5 =0.09)
F
FN
G
如果火车的速度大于此值,那么火车的受力情况会有什么改变?
如果火车的速度小于此值,那么火车的受力情况会有什么改变?
若已知拐弯速度为v,则需要轨道倾角为多少,火车才能不挤压轨道?
汽车拐弯
实例1:质量为2.0×103Kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为2.5×104N,汽车经过半径为50m的弯路时,
如果汽车的车速达到10m/s,这辆车会不会发生侧滑。
如果车速达到30m/s,车将会怎样?
如果你是一个设计师,你能否对路面进行简单的设计,以减少对于轮胎的磨损。
汽车拐弯
实例2:在高速公路的拐弯处,通常路面都是外高内低,在某路段,汽车在左转弯时,汽车左侧的路面会比右侧的路面低一些,如果汽车的质量是2×103kg,汽 车的运动可以看做是做半径为50m的圆周运动,设路面的倾斜角度10o,已知重力加速度为10m/s2,要使车轮与路面间的横向摩擦力(垂直于前进方向)等于0,汽车转弯时的车速应该是多大?(tan10o=0.18)
如果汽车的速度大于该值,汽车又没有
与路面发生相对滑动,请分析一下汽车可
能的受力情况
N
mg
Fn
飞机拐弯时,谁提供向心力呢?请大家画出图示。
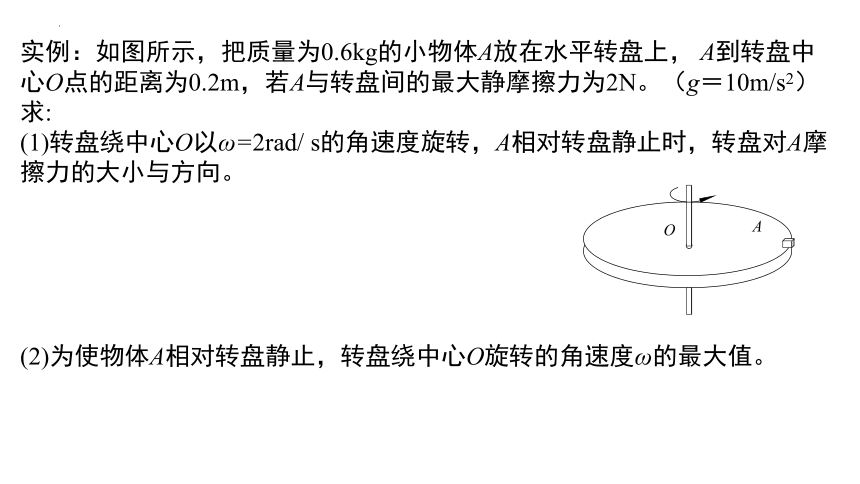
实例:如图所示,把质量为0.6kg的小物体A放在水平转盘上, A到转盘中心O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N。(g=10m/s2)求:
(1)转盘绕中心O以ω=2rad/ s的角速度旋转,A相对转盘静止时,转盘对A摩擦力的大小与方向。
O
A
(2)为使物体A相对转盘静止,转盘绕中心O旋转的角速度ω的最大值。
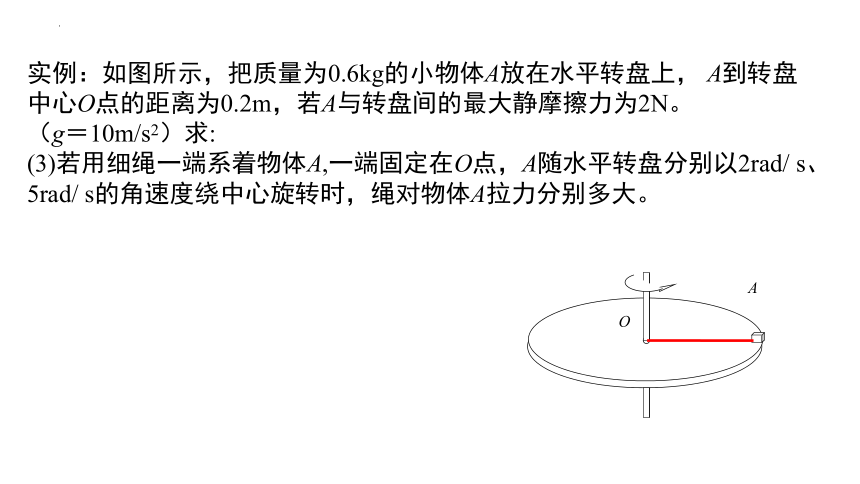
实例:如图所示,把质量为0.6kg的小物体A放在水平转盘上, A到转盘中心O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N。 (g=10m/s2)求:
(3)若用细绳一端系着物体A,一端固定在O点,A随水平转盘分别以2rad/ s、5rad/ s的角速度绕中心旋转时,绳对物体A拉力分别多大。
O
A
实例:如图所示,把质量为0.6kg的小物体A放在水平转盘上, A到转盘中心O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N。 (g=10m/s2)求:
(4)如图所示,用细绳一端系着物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围。
O
A
B
离心现象
供=需:圆周运动
供>需:向心运动
供<需:离心运动
指向圆心方向的合力
mv2/r
供
需
离心现象
转动雨伞时水滴被甩出去。
离心干燥器
转动的雨伞
洗衣机中的脱水桶高速旋转时,能把衣服上的水甩出。
作业
完成课本38-39页1-5题
竖直面的圆周运动
碗口朝下时水不流出的条件?
生活中还有相似的例子吗?
拱凹桥,超失重问题
1
A
B
C
汽车以相同的速度通过以上
ABC三点,在那点最容易爆胎?
根据哪个物理量判断?
如果在c点速度足够大将出现什么现象?
竖直面的圆周运动---应用1
拱形桥:公路上常有拱形桥, 汽车过桥时可看成圆周运动.质量为m=800 kg的小汽车通过拱桥,到达桥顶的速度为v,设桥面的圆弧半径为r=50 m,地球表面的重力加速度g=10 m/s2.
(1)如果v=5 m/s,求汽车对桥的压力.
(2)如果v不断增大,会发生什么现象
(3) v 为多大时,汽车恰好对桥没有压力而腾空
(4)对于同样的车速,为了安全,拱桥的半径是大
一些好还是小一些好
拱桥问题
拱形桥:公路上常有拱形桥, 汽车过桥时可看成圆周运动.质量为m=800 kg的小汽车通过拱桥,到达桥顶的速度为v,设桥面的圆弧半径为r=50 m,地球表面的重力加速度g=10 m/s2.
(5)如果拱桥的半径增大到等于地球半径R=6400 km,汽车要在桥面上腾空飞行,速度v为多大
(6)如果汽车(航天器)内的驾驶员(宇航员)的质量为m0,此时受到的支持力为多大 驾驶员有什么感觉
拱形桥:公路上常有拱形桥, 汽车过桥时可看成圆周运动.质量为m=800 kg的小汽车通过拱桥,到达桥顶的速度为v,设桥面的圆弧半径为r=50 m,地球表面的重力加速度g=10 m/s2.
(7)如果将拱形桥建成凹形桥,汽车以速度v通过凹形桥的最低点时,对桥的压力为多大
(8)你生活中见过凹形桥吗 为什么
(凹形桥是存在的,在过水路面有时需要修建凹形桥)
用长为l的轻绳系质量为m的小球,使其在竖直平面内作圆周运动,已知重力加速度为g.
(1)若小球过最高点的速度为v,写出绳对小球拉力F的表达式.
(2)求小球过圆周最高点的最小速度v0.
(3)若小球过最高点的速度v=2v0,求此时绳对小球的拉力F.
绳连球问题(水流星与过山车模型)
竖直面的圆周运动---应用2
(4)小球在竖直平面内做的是匀速圆周运动吗?
思考1:当杯子转动到最高点时,要让杯中的水不流出来,速度是越大越好还是越小越好?为什么?
演示水流星实验
实例:在水流星实验中,如果细绳的长度为l,水杯可以看作质点,使它在竖直平面内做圆周运动,保证水在最高处不会流出来。
画图分析受力,水不流出来的临界条件是杯底对水的压力等于零。所以完全由重力提供向心力时,就能得出在最高点的最小速度。
mg
N
思考3:如果在最高点时,细绳松弛了,水会流出来吗?
思考2:在最高点,当水对杯底存在压力时,水会流出来吗
思考4:要使水不流出来,水会受到几个力的作用?
v最小=√gl
实例:游乐场的过山车有一个竖直平面上的圆周轨道,过山车的车厢沿着圆周轨道在竖直平面内做圆周运动。将车厢想象成为一个小球,相当于小球在内轨道上做圆周运动。假设轨道半径为r,要是小球能在竖直平面内圆周运动不掉下,在最高点的最小速度是多少?
v
R
m
v
筋斗环 过山车
G
N
G
N
如果用长为l的轻杆代替轻绳固定一个质量为m的小球,使其在竖直平面内作圆周运动,已知重力加速度为g.
(1)求小球过最高点时的最小速度v.
(2)若在最高点杆对小球的作用力大小为零,求小球的速度为v0.
(3)若在最高点小球的速度为2v0,求杆对小球的作用力的大小和方向.
(4)若在最高点小球的速度为v0/2,求杆对小球的作用力的大小和方向.
杆连球问题(水流星与过山车模型)
竖直面的圆周运动---应用2
练习:飞机在竖直面内做俯冲拉起运动时,可以看作是圆周运动。如图所示,若在最低点附近作半径为R=200m的圆周运动,飞行员的质量为m=70kg,飞机经过最低点P时的速度v=360km/h,试计算在最低点P时飞行员对座位的压力是多大?(g=10m/s2)
P
FN=4200N
解:以飞行员为研究对象,分析受力.
FN
mg
(海淀区2019年期中)10.无偿献血、救死扶伤的崇高行为,是文明社会的标志之一。现代献血常采用机采成分血的方式,就是指把健康人捐献的血液,通过血液分离机分离出其中某一种成分(如血小板、粒细胞或外周血干细胞)储存起来,再将分离后的血液回输到捐献者体内。分离血液成分需要用到一种叫离心分离器的装置,其工作原理的示意图如图8所示,将血液装入离心分离器的封闭试管内,离心分离器转动时给血液提供一种“模拟重力”的环境,“模拟重力”的方向沿试管远离转轴的方向,其大小与血液中细胞的质量以及其到转轴距离成正比。
初始时试管静止,血液内离转轴同样距离处有两种细胞a、b,其密度分别为ρa和ρb,它们的大小与周围血浆密度ρ0的关系为ρa<ρ0<ρb。对于试管由静止开始绕轴旋转并不断增大转速的过程中,下列说法中正确的是 AC
A.细胞a相对试管向内侧运动,细胞b相对试管向外侧运动
B.细胞a相对试管向外侧运动,细胞b相对试管向内侧运动
C.这种离心分离器“模拟重力”对应的“重力加速度”沿转动半径方向向外侧逐渐变大
D.这种离心分离器“模拟重力”对应的“重力加速度”沿转动半径方向各处大小相同
作业
完成课本40页A组题
第四节 生活中的圆周运动
学习目标:
1.定性分析生活中圆周运动的向心力的来源
2.能分析火车转弯、汽车过拱、凹型桥的压力问题
3.能用牛顿第二定律分析圆周运动
4.知道航天器中的失重现象的本质,知道离心运动及其产生的条件
5.领会力与物体的惯性对运动状态变化所起的作用
火车车轮有突出的轮缘
火车、汽车拐弯
火车拐弯
若铁道的内外轨一样高,火车在转弯时,谁提供向心力?这个力需要多大?(已知:火车速度v为30m/s,弯道的半径R=900m,火车的质量m=8×105kg)
危害?
如何避免?
火车拐弯
铁 轨
轮 缘
外 轨
内 轨
转弯圆心
火车拐弯
若火车转弯时轨道倾角为5 ,此时要求轨道对轮缘无挤压作用,请问火车通过弯道时的最大速度是多少?(已知:转弯半径R=900m,tan5 =0.09)
F
FN
G
如果火车的速度大于此值,那么火车的受力情况会有什么改变?
如果火车的速度小于此值,那么火车的受力情况会有什么改变?
若已知拐弯速度为v,则需要轨道倾角为多少,火车才能不挤压轨道?
汽车拐弯
实例1:质量为2.0×103Kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为2.5×104N,汽车经过半径为50m的弯路时,
如果汽车的车速达到10m/s,这辆车会不会发生侧滑。
如果车速达到30m/s,车将会怎样?
如果你是一个设计师,你能否对路面进行简单的设计,以减少对于轮胎的磨损。
汽车拐弯
实例2:在高速公路的拐弯处,通常路面都是外高内低,在某路段,汽车在左转弯时,汽车左侧的路面会比右侧的路面低一些,如果汽车的质量是2×103kg,汽 车的运动可以看做是做半径为50m的圆周运动,设路面的倾斜角度10o,已知重力加速度为10m/s2,要使车轮与路面间的横向摩擦力(垂直于前进方向)等于0,汽车转弯时的车速应该是多大?(tan10o=0.18)
如果汽车的速度大于该值,汽车又没有
与路面发生相对滑动,请分析一下汽车可
能的受力情况
N
mg
Fn
飞机拐弯时,谁提供向心力呢?请大家画出图示。
实例:如图所示,把质量为0.6kg的小物体A放在水平转盘上, A到转盘中心O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N。(g=10m/s2)求:
(1)转盘绕中心O以ω=2rad/ s的角速度旋转,A相对转盘静止时,转盘对A摩擦力的大小与方向。
O
A
(2)为使物体A相对转盘静止,转盘绕中心O旋转的角速度ω的最大值。
实例:如图所示,把质量为0.6kg的小物体A放在水平转盘上, A到转盘中心O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N。 (g=10m/s2)求:
(3)若用细绳一端系着物体A,一端固定在O点,A随水平转盘分别以2rad/ s、5rad/ s的角速度绕中心旋转时,绳对物体A拉力分别多大。
O
A
实例:如图所示,把质量为0.6kg的小物体A放在水平转盘上, A到转盘中心O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N。 (g=10m/s2)求:
(4)如图所示,用细绳一端系着物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围。
O
A
B
离心现象
供=需:圆周运动
供>需:向心运动
供<需:离心运动
指向圆心方向的合力
mv2/r
供
需
离心现象
转动雨伞时水滴被甩出去。
离心干燥器
转动的雨伞
洗衣机中的脱水桶高速旋转时,能把衣服上的水甩出。
作业
完成课本38-39页1-5题
竖直面的圆周运动
碗口朝下时水不流出的条件?
生活中还有相似的例子吗?
拱凹桥,超失重问题
1
A
B
C
汽车以相同的速度通过以上
ABC三点,在那点最容易爆胎?
根据哪个物理量判断?
如果在c点速度足够大将出现什么现象?
竖直面的圆周运动---应用1
拱形桥:公路上常有拱形桥, 汽车过桥时可看成圆周运动.质量为m=800 kg的小汽车通过拱桥,到达桥顶的速度为v,设桥面的圆弧半径为r=50 m,地球表面的重力加速度g=10 m/s2.
(1)如果v=5 m/s,求汽车对桥的压力.
(2)如果v不断增大,会发生什么现象
(3) v 为多大时,汽车恰好对桥没有压力而腾空
(4)对于同样的车速,为了安全,拱桥的半径是大
一些好还是小一些好
拱桥问题
拱形桥:公路上常有拱形桥, 汽车过桥时可看成圆周运动.质量为m=800 kg的小汽车通过拱桥,到达桥顶的速度为v,设桥面的圆弧半径为r=50 m,地球表面的重力加速度g=10 m/s2.
(5)如果拱桥的半径增大到等于地球半径R=6400 km,汽车要在桥面上腾空飞行,速度v为多大
(6)如果汽车(航天器)内的驾驶员(宇航员)的质量为m0,此时受到的支持力为多大 驾驶员有什么感觉
拱形桥:公路上常有拱形桥, 汽车过桥时可看成圆周运动.质量为m=800 kg的小汽车通过拱桥,到达桥顶的速度为v,设桥面的圆弧半径为r=50 m,地球表面的重力加速度g=10 m/s2.
(7)如果将拱形桥建成凹形桥,汽车以速度v通过凹形桥的最低点时,对桥的压力为多大
(8)你生活中见过凹形桥吗 为什么
(凹形桥是存在的,在过水路面有时需要修建凹形桥)
用长为l的轻绳系质量为m的小球,使其在竖直平面内作圆周运动,已知重力加速度为g.
(1)若小球过最高点的速度为v,写出绳对小球拉力F的表达式.
(2)求小球过圆周最高点的最小速度v0.
(3)若小球过最高点的速度v=2v0,求此时绳对小球的拉力F.
绳连球问题(水流星与过山车模型)
竖直面的圆周运动---应用2
(4)小球在竖直平面内做的是匀速圆周运动吗?
思考1:当杯子转动到最高点时,要让杯中的水不流出来,速度是越大越好还是越小越好?为什么?
演示水流星实验
实例:在水流星实验中,如果细绳的长度为l,水杯可以看作质点,使它在竖直平面内做圆周运动,保证水在最高处不会流出来。
画图分析受力,水不流出来的临界条件是杯底对水的压力等于零。所以完全由重力提供向心力时,就能得出在最高点的最小速度。
mg
N
思考3:如果在最高点时,细绳松弛了,水会流出来吗?
思考2:在最高点,当水对杯底存在压力时,水会流出来吗
思考4:要使水不流出来,水会受到几个力的作用?
v最小=√gl
实例:游乐场的过山车有一个竖直平面上的圆周轨道,过山车的车厢沿着圆周轨道在竖直平面内做圆周运动。将车厢想象成为一个小球,相当于小球在内轨道上做圆周运动。假设轨道半径为r,要是小球能在竖直平面内圆周运动不掉下,在最高点的最小速度是多少?
v
R
m
v
筋斗环 过山车
G
N
G
N
如果用长为l的轻杆代替轻绳固定一个质量为m的小球,使其在竖直平面内作圆周运动,已知重力加速度为g.
(1)求小球过最高点时的最小速度v.
(2)若在最高点杆对小球的作用力大小为零,求小球的速度为v0.
(3)若在最高点小球的速度为2v0,求杆对小球的作用力的大小和方向.
(4)若在最高点小球的速度为v0/2,求杆对小球的作用力的大小和方向.
杆连球问题(水流星与过山车模型)
竖直面的圆周运动---应用2
练习:飞机在竖直面内做俯冲拉起运动时,可以看作是圆周运动。如图所示,若在最低点附近作半径为R=200m的圆周运动,飞行员的质量为m=70kg,飞机经过最低点P时的速度v=360km/h,试计算在最低点P时飞行员对座位的压力是多大?(g=10m/s2)
P
FN=4200N
解:以飞行员为研究对象,分析受力.
FN
mg
(海淀区2019年期中)10.无偿献血、救死扶伤的崇高行为,是文明社会的标志之一。现代献血常采用机采成分血的方式,就是指把健康人捐献的血液,通过血液分离机分离出其中某一种成分(如血小板、粒细胞或外周血干细胞)储存起来,再将分离后的血液回输到捐献者体内。分离血液成分需要用到一种叫离心分离器的装置,其工作原理的示意图如图8所示,将血液装入离心分离器的封闭试管内,离心分离器转动时给血液提供一种“模拟重力”的环境,“模拟重力”的方向沿试管远离转轴的方向,其大小与血液中细胞的质量以及其到转轴距离成正比。
初始时试管静止,血液内离转轴同样距离处有两种细胞a、b,其密度分别为ρa和ρb,它们的大小与周围血浆密度ρ0的关系为ρa<ρ0<ρb。对于试管由静止开始绕轴旋转并不断增大转速的过程中,下列说法中正确的是 AC
A.细胞a相对试管向内侧运动,细胞b相对试管向外侧运动
B.细胞a相对试管向外侧运动,细胞b相对试管向内侧运动
C.这种离心分离器“模拟重力”对应的“重力加速度”沿转动半径方向向外侧逐渐变大
D.这种离心分离器“模拟重力”对应的“重力加速度”沿转动半径方向各处大小相同
作业
完成课本40页A组题
