人教版九年级下册数学达标检测卷—第二十七章 相似形(含答案)
文档属性
| 名称 | 人教版九年级下册数学达标检测卷—第二十七章 相似形(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 08:35:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学第二十七章达标检测卷
【检测内容:第二十七章 相似形 满分:120分】
一、选择题(每小题3分,共30分)
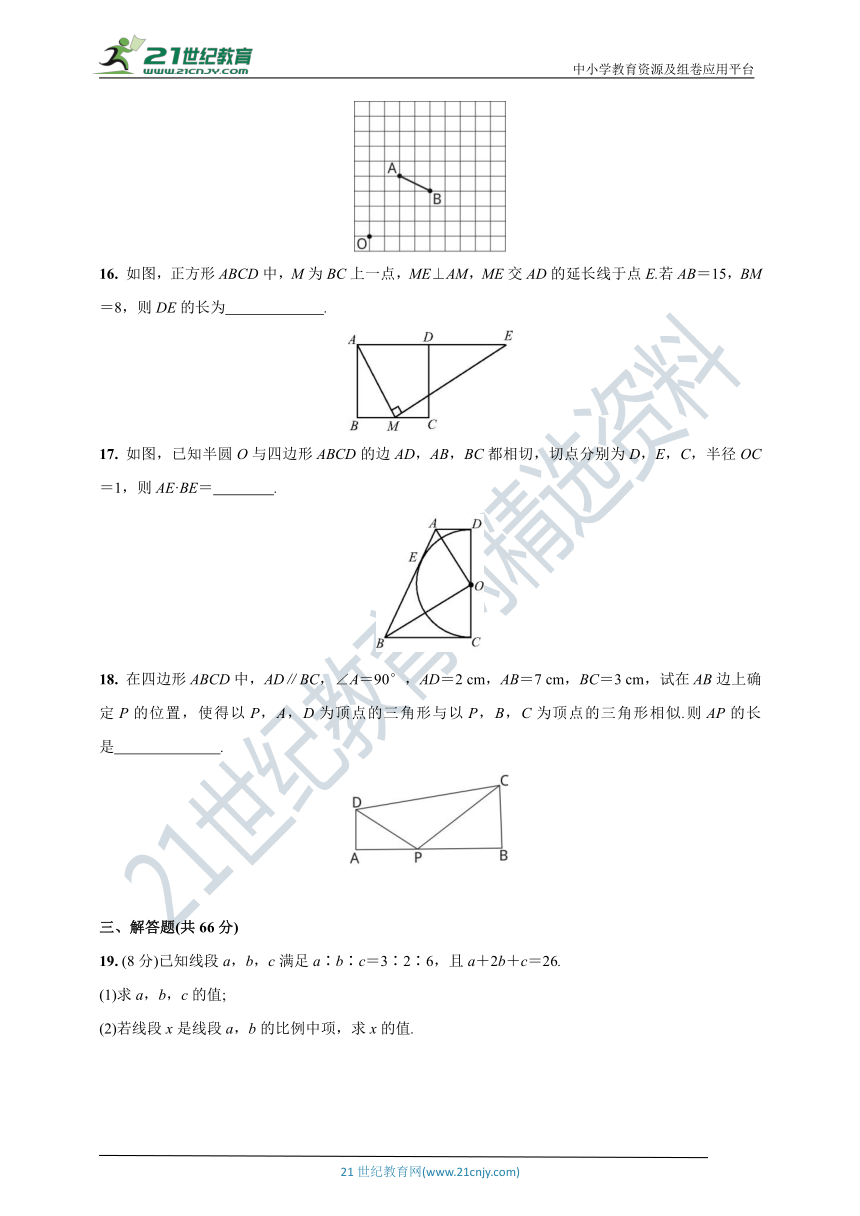
1. 若a∶b=c∶d,则下列各式成立的是( )
A.a∶d=c∶b B.b∶d=c∶a C.= D.=(b+d≠0)
2. 在设计人体雕像时,使雕像的上部与下部的高度比等于下部与全身的高度比,可以增加视觉美感.按此比例,如果雕像的高为2 m,设它的下部的高度应设计为x m,则x满足的关系式为( )
A.(1-x)∶x=1∶x B.x∶(2-x)=(2-x)∶2
C.(1-x)∶x=x∶1 D.(2-x)∶x=x∶2
3. 若两个相似三角形的面积比为3∶5,则它们的对应角的平分线的比为( )
A.∶ B.3∶5 C.1∶5 D.9∶25
4. 如图,在△ABC中,点D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于点E,则BE∶EC的值是( )
A.1∶2 B.1∶3 C.1∶4 D.2∶3
5. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似( )
A.①处 B.②处 C.③处 D.④处
6. 如图,AB为☉O的直径,BC为☉O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是☉O的切线;②CO⊥DB;③△EDA∽△EBD;④ED·BC=BO·BE.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
7. 如图,在平面直角坐标系中,直线y=-x+2和x轴、y轴分别交于B,A两点,在第二象限内找一点P,使△PAO和△AOB相似,这样的三角形有( )
A.2个 B.3个 C.4个 D.5个
8. 如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的.若△ABC与△A'B'C'的面积之比是16∶9,则OA∶OA'为( )
A.4∶3 B.3∶4 C.9∶16 D.16∶9
9. 如图所示,一架投影机插入胶片后图象可投到屏幕上.已知胶片与屏幕平行,点A为光源,与胶片BC的距离为0.1米,胶片BC的高为0.038米.若需要投影后的图象DE的高为1.9米,则投影机光源离屏幕大约为( )
A.6米 B.5米 C.4米 D.3米
10. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5
二、填空题(每小题3分,共24分)
11. 已知==,且a+b-2c=6,则a的值为 .
12. 如图,已知∠ACB=∠ADC=90°,AD=CD=2,当AB的长为 时,△ACB与△ADC相似.
13. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G.若AB=2,CD=3,则GH的长为 .
14. 如图,已知△ABO的顶点A(-4,8),以原点O为位似中心,把△ABO缩小为原来的,则与点A对应的点A'的坐标是 .
15. 如图,由边长为1个单位长度的小正方形组成的网格中,先以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),再将线段A1B1绕点B1逆时针旋转90°,得到线段A2B1,则四边形AA1B1A2的面积是 个平方单位.
16. 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=15,BM=8,则DE的长为 .
17. 如图,已知半圆O与四边形ABCD的边AD,AB,BC都相切,切点分别为D,E,C,半径OC=1,则AE·BE= .
18. 在四边形ABCD中,AD∥BC,∠A=90°,AD=2 cm,AB=7 cm,BC=3 cm,试在AB边上确定P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.则AP的长是 .
三、解答题(共66分)
19. (8分)已知线段a,b,c满足a∶b∶c=3∶2∶6,且a+2b+c=26.
(1)求a,b,c的值;
(2)若线段x是线段a,b的比例中项,求x的值.
20. (8分)如图,在Rt△CBA中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线交BC于点E,连接OE.
(1)求证:△DBE是等腰三角形.
(2)求证:△COE∽△CAB.
21. (9分)如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD. EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AE的长.
22. (9分)如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)试说明:△ABD≌△BCE.
(2)△EAF与△EBA相似吗 请说明理由.
23. (10分)如图,点B,D,E在一条直线上,BE与AC相交于点F,==.
(1)求证:∠BAD=∠CAE.
(2)若∠BAD=21°,求∠EBC的度数.
(3)连接EC,求证:△ABD∽△ACE.
24. (10分)如图,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF.
(2)求证:△ABG∽△CFG.
25. (12分)如图,已知四边形ABCD是菱形,E是对角线AC上一点,连接BE并延长,交AD于点F,交CD的延长线于点G,连接DE.
(1)求证:△ABE≌△ADE.
(2)求证:EB2=EF·EG.
(3)若菱形ABCD的边长为4,∠ABC=60°,AE∶EC=1∶3,求BG的长.
参 考 答 案
1. D 2. D 3. A 4. B 5. B 6. A 7. C 8. A 9. B 10. B
11. 12 12. 4 13. 14. (-1,2)或(1,-2) 15. 20 16. 17. 1 18. cm或1 cm或6 cm
19. 解:(1)∵a∶b∶c=3∶2∶6,∴设a=3k,b=2k,c=6k. ∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12.
(2)∵x是a,b的比例中项,∴x2=ab,∴x2=4×6,∴x=2或x=-2(舍去),即x的值为2.
20. 证明:(1)连接OD.∵DE是☉O的切线,∴∠ODE=90°,∴∠ADO+∠BDE=90°.∵∠ACB=90°,∴∠CAB+∠CBA=90°.∵OA=OD,∴∠CAB=∠ADO,∴∠BDE=∠CBA,∴EB=ED,∴△DBE是等腰三角形.
(2)∵∠ACB=90°,AC是☉O的直径,∴CB是☉O的切线.∵DE是☉O的切线,∴DE=EC.∵EB=ED,∴EC=EB.∵OA=OC,∴OE∥AB,∴△COE∽△CAB.
21. 解:(1)∵四边形ABCD是矩形,点E在BA的延长线上,∴∠EAF=∠DAB=90°.又AE=AD,AF=AB,∴△AEF≌△ADB,∠AEF=∠ADB,∴∠GEB+∠GBE=∠ADB+∠ABD=90°,即∠EGB=90°,故BD⊥EC.
(2)由矩形性质知AE∥CD,∴∠AEF=∠DCF,∠EAF=∠CDF,∴△AEF∽△DCF,=,即AE·DF=AF·DC.设AE=AD=a(a>0),则有a·(a-1)=1,化简得a2-a-1=0,解得a=或(舍),∴AE的长为.
22. 解:(1)∵△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE.又∵BD=CE,∴△ABD≌△BCE.
(2)相似. 理由:∵△ABD≌△BCE,∴∠BAD=∠CBE,∴∠BAC-∠BAD=∠CBA-∠CBE,∴∠EAF=∠EBA.又∵∠AEF=∠BEA,∴△EAF∽△EBA.
23. 解:(1)∵==,∴△ABC∽△ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE.
(2)∵△ABC∽△ADE,∴∠ABC=∠ADE.∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,∴∠EBC=∠BAD=21°.
(3)由(1)知∠BAD=∠CAE.又∵=,即=,∴△ABD∽△ACE.
24. 证明:(1)依题意可知∠ADC=∠EDF=90°,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF.∵AD=CD,△DEF为等腰三角形,即DE=DF,∴△DAE≌△DCF.
(2)由题知∠ABG=90°,△EDF为等腰直角三角形,∴∠DEF=∠DFE=45°.∵∠DEF=∠DFC=45°,∴∠DFC+∠DFE=∠CFG=∠ABG=90°.∵∠AGB=∠CGF,∴△ABG∽△CFG.
25. 解:(1)∵四边形ABCD是菱形,∴AB=AD,∠BAC=∠DAC,又AE=AE,∴△ABE≌△ADE.
(2)∵AB∥CG,∴∠ABG=∠EGD,由(1)得△ABE≌△ADE,∴ED=EB,∠ABG=∠ADE,∴∠EGD=∠ADE.∵∠FED=∠DEG,∴△EDF∽△EGD,∴=,∴ED2=EF·EG,∴EB2=EF·EG.
(3)∵AB=BC,∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=4.连接BD,交AC于点O,则AC⊥BD,OA=OC=2,OB=2.∵AE∶EC=1∶3,∴AE=OE=1,∴BE==.∵AB∥CG,∴△ABE∽△CGE,∴==,∴EG=3,∴BG=BE+EG=4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学第二十七章达标检测卷
【检测内容:第二十七章 相似形 满分:120分】
一、选择题(每小题3分,共30分)
1. 若a∶b=c∶d,则下列各式成立的是( )
A.a∶d=c∶b B.b∶d=c∶a C.= D.=(b+d≠0)
2. 在设计人体雕像时,使雕像的上部与下部的高度比等于下部与全身的高度比,可以增加视觉美感.按此比例,如果雕像的高为2 m,设它的下部的高度应设计为x m,则x满足的关系式为( )
A.(1-x)∶x=1∶x B.x∶(2-x)=(2-x)∶2
C.(1-x)∶x=x∶1 D.(2-x)∶x=x∶2
3. 若两个相似三角形的面积比为3∶5,则它们的对应角的平分线的比为( )
A.∶ B.3∶5 C.1∶5 D.9∶25
4. 如图,在△ABC中,点D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于点E,则BE∶EC的值是( )
A.1∶2 B.1∶3 C.1∶4 D.2∶3
5. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似( )
A.①处 B.②处 C.③处 D.④处
6. 如图,AB为☉O的直径,BC为☉O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是☉O的切线;②CO⊥DB;③△EDA∽△EBD;④ED·BC=BO·BE.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
7. 如图,在平面直角坐标系中,直线y=-x+2和x轴、y轴分别交于B,A两点,在第二象限内找一点P,使△PAO和△AOB相似,这样的三角形有( )
A.2个 B.3个 C.4个 D.5个
8. 如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的.若△ABC与△A'B'C'的面积之比是16∶9,则OA∶OA'为( )
A.4∶3 B.3∶4 C.9∶16 D.16∶9
9. 如图所示,一架投影机插入胶片后图象可投到屏幕上.已知胶片与屏幕平行,点A为光源,与胶片BC的距离为0.1米,胶片BC的高为0.038米.若需要投影后的图象DE的高为1.9米,则投影机光源离屏幕大约为( )
A.6米 B.5米 C.4米 D.3米
10. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5
二、填空题(每小题3分,共24分)
11. 已知==,且a+b-2c=6,则a的值为 .
12. 如图,已知∠ACB=∠ADC=90°,AD=CD=2,当AB的长为 时,△ACB与△ADC相似.
13. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G.若AB=2,CD=3,则GH的长为 .
14. 如图,已知△ABO的顶点A(-4,8),以原点O为位似中心,把△ABO缩小为原来的,则与点A对应的点A'的坐标是 .
15. 如图,由边长为1个单位长度的小正方形组成的网格中,先以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),再将线段A1B1绕点B1逆时针旋转90°,得到线段A2B1,则四边形AA1B1A2的面积是 个平方单位.
16. 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=15,BM=8,则DE的长为 .
17. 如图,已知半圆O与四边形ABCD的边AD,AB,BC都相切,切点分别为D,E,C,半径OC=1,则AE·BE= .
18. 在四边形ABCD中,AD∥BC,∠A=90°,AD=2 cm,AB=7 cm,BC=3 cm,试在AB边上确定P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.则AP的长是 .
三、解答题(共66分)
19. (8分)已知线段a,b,c满足a∶b∶c=3∶2∶6,且a+2b+c=26.
(1)求a,b,c的值;
(2)若线段x是线段a,b的比例中项,求x的值.
20. (8分)如图,在Rt△CBA中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线交BC于点E,连接OE.
(1)求证:△DBE是等腰三角形.
(2)求证:△COE∽△CAB.
21. (9分)如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD. EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AE的长.
22. (9分)如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)试说明:△ABD≌△BCE.
(2)△EAF与△EBA相似吗 请说明理由.
23. (10分)如图,点B,D,E在一条直线上,BE与AC相交于点F,==.
(1)求证:∠BAD=∠CAE.
(2)若∠BAD=21°,求∠EBC的度数.
(3)连接EC,求证:△ABD∽△ACE.
24. (10分)如图,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF.
(2)求证:△ABG∽△CFG.
25. (12分)如图,已知四边形ABCD是菱形,E是对角线AC上一点,连接BE并延长,交AD于点F,交CD的延长线于点G,连接DE.
(1)求证:△ABE≌△ADE.
(2)求证:EB2=EF·EG.
(3)若菱形ABCD的边长为4,∠ABC=60°,AE∶EC=1∶3,求BG的长.
参 考 答 案
1. D 2. D 3. A 4. B 5. B 6. A 7. C 8. A 9. B 10. B
11. 12 12. 4 13. 14. (-1,2)或(1,-2) 15. 20 16. 17. 1 18. cm或1 cm或6 cm
19. 解:(1)∵a∶b∶c=3∶2∶6,∴设a=3k,b=2k,c=6k. ∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12.
(2)∵x是a,b的比例中项,∴x2=ab,∴x2=4×6,∴x=2或x=-2(舍去),即x的值为2.
20. 证明:(1)连接OD.∵DE是☉O的切线,∴∠ODE=90°,∴∠ADO+∠BDE=90°.∵∠ACB=90°,∴∠CAB+∠CBA=90°.∵OA=OD,∴∠CAB=∠ADO,∴∠BDE=∠CBA,∴EB=ED,∴△DBE是等腰三角形.
(2)∵∠ACB=90°,AC是☉O的直径,∴CB是☉O的切线.∵DE是☉O的切线,∴DE=EC.∵EB=ED,∴EC=EB.∵OA=OC,∴OE∥AB,∴△COE∽△CAB.
21. 解:(1)∵四边形ABCD是矩形,点E在BA的延长线上,∴∠EAF=∠DAB=90°.又AE=AD,AF=AB,∴△AEF≌△ADB,∠AEF=∠ADB,∴∠GEB+∠GBE=∠ADB+∠ABD=90°,即∠EGB=90°,故BD⊥EC.
(2)由矩形性质知AE∥CD,∴∠AEF=∠DCF,∠EAF=∠CDF,∴△AEF∽△DCF,=,即AE·DF=AF·DC.设AE=AD=a(a>0),则有a·(a-1)=1,化简得a2-a-1=0,解得a=或(舍),∴AE的长为.
22. 解:(1)∵△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE.又∵BD=CE,∴△ABD≌△BCE.
(2)相似. 理由:∵△ABD≌△BCE,∴∠BAD=∠CBE,∴∠BAC-∠BAD=∠CBA-∠CBE,∴∠EAF=∠EBA.又∵∠AEF=∠BEA,∴△EAF∽△EBA.
23. 解:(1)∵==,∴△ABC∽△ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE.
(2)∵△ABC∽△ADE,∴∠ABC=∠ADE.∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,∴∠EBC=∠BAD=21°.
(3)由(1)知∠BAD=∠CAE.又∵=,即=,∴△ABD∽△ACE.
24. 证明:(1)依题意可知∠ADC=∠EDF=90°,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF.∵AD=CD,△DEF为等腰三角形,即DE=DF,∴△DAE≌△DCF.
(2)由题知∠ABG=90°,△EDF为等腰直角三角形,∴∠DEF=∠DFE=45°.∵∠DEF=∠DFC=45°,∴∠DFC+∠DFE=∠CFG=∠ABG=90°.∵∠AGB=∠CGF,∴△ABG∽△CFG.
25. 解:(1)∵四边形ABCD是菱形,∴AB=AD,∠BAC=∠DAC,又AE=AE,∴△ABE≌△ADE.
(2)∵AB∥CG,∴∠ABG=∠EGD,由(1)得△ABE≌△ADE,∴ED=EB,∠ABG=∠ADE,∴∠EGD=∠ADE.∵∠FED=∠DEG,∴△EDF∽△EGD,∴=,∴ED2=EF·EG,∴EB2=EF·EG.
(3)∵AB=BC,∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=4.连接BD,交AC于点O,则AC⊥BD,OA=OC=2,OB=2.∵AE∶EC=1∶3,∴AE=OE=1,∴BE==.∵AB∥CG,∴△ABE∽△CGE,∴==,∴EG=3,∴BG=BE+EG=4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
