2021-2022学年湖南省衡阳市衡南县部分学校九年级(下)入学数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年湖南省衡阳市衡南县部分学校九年级(下)入学数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 880.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 10:58:30 | ||
图片预览




文档简介
2021-2022学年湖南省衡阳市衡南县部分学校九年级(下)入学数学试卷
一、选择题(共12小题,满分36分,每小题3分)
1.式子成立的条件是( )
A.a=0 B.a≥3 C.a≤3 D.a=3
2.已知两个相似三角形的相似比为4:9,则这两个三角形的对应高的比为( )
A.2:3 B.4:9 C.16:81 D.9:4
3.一元二次方程x2﹣2x﹣3=0配方后可变形为( )
A.(x+1)2=4 B.(x﹣1)2=4 C.(x+1)2=16 D.(x﹣1)2=16
4.如图,直线a∥b∥c,直线m、n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=3,BC=5,DF=12,则DE的值为( )
A. B.4 C. D.
5.一块正方形的瓷砖,面积为50cm2,它的边长大约在( )
A.4cm~5cm之间 B.5cm~6cm之间
C.6cm~7cm之间 D.7cm~8cm之间
6.在Rt△ABC中,∠C=90°,cosA=,则sinA=( )
A. B. C. D.
7.下列各式计算正确的是( )
A.=﹣2 B.(+)(﹣)=3
C.=+ D.=×
8.在美丽乡村的建设中,某村加大对绿化的投资.2016年用于绿化投资50万元,2018年用于绿化投资72万元,求这两年绿化投资的年平均增长率.设这两年绿化投资的年平均增长率为x,根据题意所列方程为( )
A.50x2=72 B.50(1+x)=7
C.50(1+x)2=72 D.50(1+x)+20(1+x)2=72
9.如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;
④△ABC与△DEF的面积比为4:1.
A.1 B.2 C.3 D.4
10.若方程x2+4x+a=0无实根,化简等于( )
A.4﹣a B.a﹣4 C.﹣(a+4) D.无法确定
11.如图,O是△ABC的重心,则图中与△ABD面积相等的三角形个数为( )
A.3 B.4 C.5 D.6
12.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从点A出发沿AB以1cm/s的速度向点B运动,同时动点E从点C出发沿CA以2cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是( )
A.3s或4.8s B.3s C.4.5s D.4.5s或4.8s
二、填空题(共6小题,满分18分。每小题3分)
13.计算的结果是 .
14.点A(5,m)和点B(n,﹣3)关于原点对称,则m+n= .
15.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长是 .
16.若关于x的一元二次方程kx2﹣(k+2)x+k2+k=0有一个根为0,则k的值为 .
17.现有四张外观一样的卡片,背面朝上,正面分别有一个二次根式:、、、,从中任取一张卡片,再从剩下的卡片中又抽取一张,则两次所取卡片上的二次根式是同类二次根式的概率是 .
18.已知a是x2+x﹣2=0的根,则代数式(a2+a)(a﹣+3)的值为 .
三、解答题(共8小题,满分66分)
19.计算:(﹣1)2021+2sin60°+|﹣|﹣.
20.解方程:3x(x+2)=5(x+2)
21.如图,在 ABCD中,DE⊥AB于点E,交AC于点F,且AE:EB=1:2.
(1)求证:△AEF∽△CDF;
(2)求△AEF与△AFD的面积比.
22.用一段长为30m的篱笆围成一个靠墙的矩形菜园,墙的长度为18m.
(1)设垂直于墙的一边长为xm,则是菜园的面积为 ;
(2)若菜园的面积为100m2,求x的值.
23.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
24.如图,楼高AB为26米,从楼顶A处测得旗杆顶C的俯角为60°,又从距离楼底B处4m的一窗口E处测得旗杆顶C的仰角为45°,求旗杆CD的高.
25.已知关于x的一元二次方程x2﹣(8+k)x+8k=0.
(1)证明:无论k取任何实数,方程总有实数根.
(2)若,求k的值.
(3)若等腰三角形的一边长为5,另两边长恰好是这个方程的两个根,求这个等腰三角形的周长.
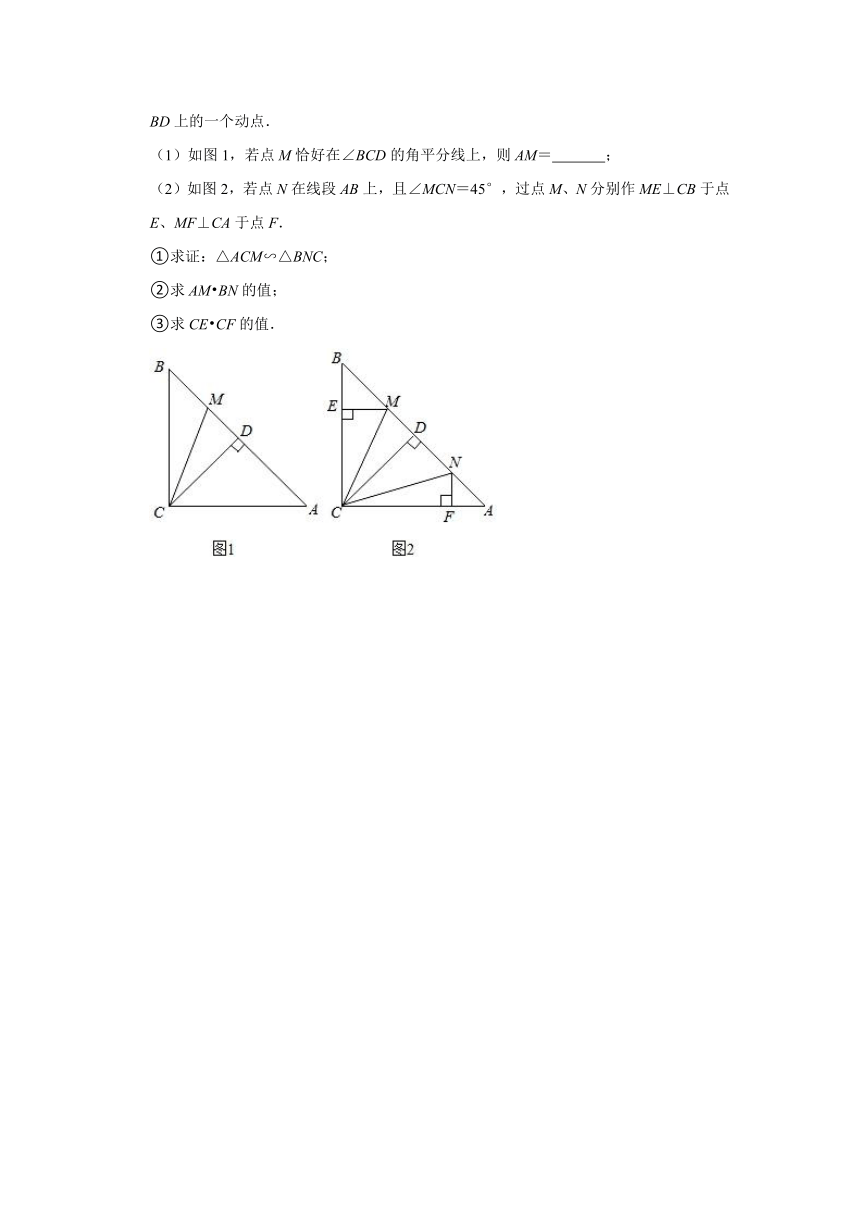
26.如图,已知Rt△ABC中,∠ACB=90°,CA=CB=4,CD⊥AB于点D,点M是线段BD上的一个动点.
(1)如图1,若点M恰好在∠BCD的角平分线上,则AM= ;
(2)如图2,若点N在线段AB上,且∠MCN=45°,过点M、N分别作ME⊥CB于点E、MF⊥CA于点F.
①求证:△ACM∽△BNC;
②求AM BN的值;
③求CE CF的值.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.式子成立的条件是( )
A.a=0 B.a≥3 C.a≤3 D.a=3
【分析】由二次根式的定义,被开方数是非负数,即可求解.
解:当a﹣3≥0时,成立,
∴a≥3,
故选:B.
2.已知两个相似三角形的相似比为4:9,则这两个三角形的对应高的比为( )
A.2:3 B.4:9 C.16:81 D.9:4
【分析】直接利用相似三角形的性质求解.
解:因为两个相似三角形的相似比为4:9,
所以则这两个三角形的对应高的比为4:9.
故选:B.
3.一元二次方程x2﹣2x﹣3=0配方后可变形为( )
A.(x+1)2=4 B.(x﹣1)2=4 C.(x+1)2=16 D.(x﹣1)2=16
【分析】根据配方法即可求出答案.
解:∵x2﹣2x﹣3=0,
∴x2﹣2x+1=4,
∴(x﹣1)2=4,
故选:B.
4.如图,直线a∥b∥c,直线m、n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=3,BC=5,DF=12,则DE的值为( )
A. B.4 C. D.
【分析】由平行线的性质得出=,即=,解方程即可得出结果.
解:∵DF=12,
∴EF=12﹣DE,
∵a∥b∥c,
∴=,
即:=,
解得:DE=,
故选:C.
5.一块正方形的瓷砖,面积为50cm2,它的边长大约在( )
A.4cm~5cm之间 B.5cm~6cm之间
C.6cm~7cm之间 D.7cm~8cm之间
【分析】根据正方形的面积公式求得:边长×边长=50,所以边长=(取正值).
解:设正方形的边长为a,则
a2=50,
∴,
∵正方形的边长a>0,
∴=,
又∵<,即7<<8,
7<a<8;
故选:D.
6.在Rt△ABC中,∠C=90°,cosA=,则sinA=( )
A. B. C. D.
【分析】根据同一锐角的正弦与余弦的平方和是1,即可求解.
解:∵sin2A+cos2A=1,即sin2A+()2=1,
∴sin2A=,
∴sinA=或﹣(舍去),
∴sinA=.
故选:C.
7.下列各式计算正确的是( )
A.=﹣2 B.(+)(﹣)=3
C.=+ D.=×
【分析】直接利用二次根式混合运算法则结合二次根式的性质分别化简得出答案.
解:A.=2,故此选项不合题意;
B.(+)(﹣)=3,故此选项符合题意;
C.=,故此选项不合题意;
D.=×,故此选项不合题意;
故选:B.
8.在美丽乡村的建设中,某村加大对绿化的投资.2016年用于绿化投资50万元,2018年用于绿化投资72万元,求这两年绿化投资的年平均增长率.设这两年绿化投资的年平均增长率为x,根据题意所列方程为( )
A.50x2=72 B.50(1+x)=7
C.50(1+x)2=72 D.50(1+x)+20(1+x)2=72
【分析】设这两年绿化投资的年平均增长率为x,根据2016年及2018年用于绿化投资的金额,即可得出关于x的一元二次方程,此题得解.
解:设这两年绿化投资的年平均增长率为x,
依题意,得:50(1+x)2=72.
故选:C.
9.如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;
④△ABC与△DEF的面积比为4:1.
A.1 B.2 C.3 D.4
【分析】根据位似图形的性质,得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出 ②△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
解:根据位似性质得出①△ABC与△DEF是位似图形,
②△ABC与△DEF是相似图形,
∵将△ABC的三边缩小的原来的,
∴△ABC与△DEF的周长比为2:1,
故③选项错误,
根据面积比等于相似比的平方,
∴④△ABC与△DEF的面积比为4:1.
故选:C.
10.若方程x2+4x+a=0无实根,化简等于( )
A.4﹣a B.a﹣4 C.﹣(a+4) D.无法确定
【分析】先根据方程无实根判断出a的取值范围,再代入原代数式计算即可.
解:∵方程x2+4x+a=0无实根,∴Δ=42﹣4a<0,∴a>4.
==|a﹣4|,
∵a>4,∴|a﹣4|=a﹣4.
故选:B.
11.如图,O是△ABC的重心,则图中与△ABD面积相等的三角形个数为( )
A.3 B.4 C.5 D.6
【分析】根据题干条件D、E、F为△ABC三边的中点,故得BD=CD,又知△ABD与△ADC的高相等,于是得到△ABD与△ACD的面积相等并且为△ABC面积的一半,同理可得△CBE与△ABE,△ACF与△BCF面积相等,并且都为△ABC面积的一半,即可求出与△ABD面积相等的三角形个数,
解:∵O是△ABC的重心,
∴BD=CD,
又∵△ABD与△ADC的高相等,
∴△ABD与△ACD的面积相等=S△ABC,
同理可知:△CBE与△ABE,△ACF与△BCF面积相等,并且都为△ABC面积的一半,
∴图中与△ABD面积相等的三角形个数为5个,
故选:C.
12.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从点A出发沿AB以1cm/s的速度向点B运动,同时动点E从点C出发沿CA以2cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是( )
A.3s或4.8s B.3s C.4.5s D.4.5s或4.8s
【分析】如果以点A、D、E为顶点的三角形与△ABC相似,由于A与A对应,那么分两种情况:①D与B对应;②D与C对应.根据相似三角形的性质分别作答.
解:如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,
则AD=t(cm),CE=2t(cm),AE=AC﹣CE=(12﹣2t)(cm),
①当D与B对应时,有△ADE∽△ABC,
∴AD:AB=AE:AC,
∴t:6=(12﹣2t):12,
∴t=3;
②当D与C对应时,有△ADE∽△ACB,
∴AD:AC=AE:AB,
∴t:12=(12﹣2t):6,
∴t=4.8,
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒,
故选:A.
二、填空题(共6小题,满分18分。每小题3分)
13.计算的结果是 2 .
【分析】直接化简二次根式进而合并得出答案.
解:原式=+
=2.
故答案为:2.
14.点A(5,m)和点B(n,﹣3)关于原点对称,则m+n= ﹣2 .
【分析】平面内关于原点对称的点的坐标特点为:横坐标、纵坐标都互为相反数,由此可求解.
解:∵点A(5,m)和点B(n,﹣3)关于原点对称,
∴m=3,n=﹣5,
∴m+n=3+(﹣5)=﹣2,
故答案为:﹣2.
15.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长是 5 .
【分析】因为四条线段成比例,可根据前两条线段,确定其比例,进而求出x的值.
解:∵m:n=2:8=1:4,
∴x:y=1:4,
∵y=20,
∴x=5.
16.若关于x的一元二次方程kx2﹣(k+2)x+k2+k=0有一个根为0,则k的值为 ﹣1 .
【分析】根据一元二次方程的解的定义得到k2+k=0,再解关于k的方程,然后根据一元二次方程的定义确定k的值.
解:把x=0代入一元二次方程kx2﹣(k+2)x+k2+k=0得k2+k=0,
解得k1=0,k2=﹣1,
而k≠0,
所以k的值为﹣1.
故答案为:﹣1.
17.现有四张外观一样的卡片,背面朝上,正面分别有一个二次根式:、、、,从中任取一张卡片,再从剩下的卡片中又抽取一张,则两次所取卡片上的二次根式是同类二次根式的概率是 .
【分析】将、、、四张卡片分别记作A、B、C、D,其中A、C是同类二次根式,B、D是同类二次根式,画树状图列出所有等可能结果,找到符合条件的结果数,根据概率公式求解即可.
解:=2,=5,=3,
将、、、四张卡片分别记作A、B、C、D,
其中A、C是同类二次根式,B、D是同类二次根式,
画树状图如下:
共有12种等可能的结果,其中两次所取卡片上的二次根式是同类二次根式的有4种结果,
所以两次所取卡片上的二次根式是同类二次根式的概率为=,
故答案为:.
18.已知a是x2+x﹣2=0的根,则代数式(a2+a)(a﹣+3)的值为 4 .
【分析】先利用一元二次方程根的定义得到a2=﹣a+2,a2+a=2,再利用通分和整体代入的方法进行计算即可.
解:∵a是x2+x﹣2=0的根,
∴a2+a﹣2=0.
∴a2﹣2=﹣a,a2+a=2.
∴(a2+a)(a﹣+3)
=2×(+3)
=2×(﹣+3)
=4.
故答案是:4.
三、解答题(共8小题,满分66分)
19.计算:(﹣1)2021+2sin60°+|﹣|﹣.
【分析】首先计算乘方、特殊角的三角函数值、开方和绝对值,然后计算乘法,最后从左向右依次计算,求出算式的值即可.
解:(﹣1)2021+2sin60°+|﹣|﹣
=﹣1+2×+﹣2
=﹣1++﹣2
=﹣1.
20.解方程:3x(x+2)=5(x+2)
【分析】本题可先对方程进行移项,然后提取公因式x+2,将原式化为两式相乘的形式,再根据“两式相乘值为0,这两式中至少有一式值为0”来解题.
解:原方程可化为
3x(x+2)﹣5(x+2)=0,
(3x﹣5)(x+2)=0,
解得x1=﹣2,.
21.如图,在 ABCD中,DE⊥AB于点E,交AC于点F,且AE:EB=1:2.
(1)求证:△AEF∽△CDF;
(2)求△AEF与△AFD的面积比.
【分析】(1)由平行四边形的性质可得CD∥AB,可得结论;
(2)由相似三角形的性质可得,即可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴△AEF∽△CDF;
(2)解:∵AE:EB=1:2,
∴AE:AB=1:3,
∴AE:CD=1:3,
∵△AEF∽△CDF,
∴,
∵S△AEF=,S△AFD=,
∴S△AEF:S△AFD=EF:DF=.
22.用一段长为30m的篱笆围成一个靠墙的矩形菜园,墙的长度为18m.
(1)设垂直于墙的一边长为xm,则是菜园的面积为 x(30﹣2x)m2 ;
(2)若菜园的面积为100m2,求x的值.
【分析】(1)设垂直于墙的一边长为xm,则平行于墙的一边长为(30﹣2x)m,利用矩形的面积计算公式,即可用含x的代数式表示出菜园的面积;
(2)根据菜园的面积为100m2,即可得出关于x的一元二次方程,解之即可得出x的值,再结合墙的长度为18m,即可确定x的值.
解:(1)设垂直于墙的一边长为xm,则平行于墙的一边长为(30﹣2x)m,
∴菜园的面积为x(30﹣2x)m2.
故答案为:x(30﹣2x)m2.
(2)依题意得:x(30﹣2x)m2=100,
整理得:x2﹣15x+50=0,
解得:x1=5,x2=10.
当x=5时,30﹣2x=30﹣2×5=20>18,不合题意,舍去;
当x=10时,30﹣2x=30﹣2×10=10<18,符合题意.
答:x的值为10.
23.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 200 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 81° ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
【分析】(1)用支付宝、现金及其他的人数和除以这三者的百分比之和可得总人数;
(2)用360°乘以“支付宝”人数所占比例即可得;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人恰好选择同一种支付方式的情况,再利用概率公式即可求得答案.
解:(1)这次活动共调查的人数为30÷15%=200(人),
故答案为:200;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为360°×=81°,
故答案为:81°;
(3)将微信记为A,支付宝记为B,银行卡记为C,列表格如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能性的结果,其中两人恰好选择同一种支付方式的结果有3种,
则P(两人恰好选择同一种支付方式)=.
24.如图,楼高AB为26米,从楼顶A处测得旗杆顶C的俯角为60°,又从距离楼底B处4m的一窗口E处测得旗杆顶C的仰角为45°,求旗杆CD的高.
【分析】首先利用图形得出BE=4m,∠FEC=45°,∠FAC=30°,则AE=22m,进而利用锐角三角函数关系求出即可.
解:过点C作CF⊥AB于点F,根据题意可得:
BE=4m,∠FEC=45°,∠FAC=30°,则AE=22m
设EF=xm,则FC=xm,AF=(22﹣x)m,
故tan30°===,
解得:x=11﹣11,
故DC=11﹣11+4=(11﹣7)m
答:旗杆CD的高为(11﹣7)m.
25.已知关于x的一元二次方程x2﹣(8+k)x+8k=0.
(1)证明:无论k取任何实数,方程总有实数根.
(2)若,求k的值.
(3)若等腰三角形的一边长为5,另两边长恰好是这个方程的两个根,求这个等腰三角形的周长.
【分析】(1)根据根的判别式即可得到结论;
(2)先计算Δ=(8+k)2﹣4×8k,整理得到Δ=(k﹣8)2,根据非负数的性质得到△≥0,然后根据△的意义即可得到结论;
(3)先解出原方程的解为x1=k,x2=8,然后分类讨论:腰长为5时,则k=5;当底边为5时,则得到k=8,然后分别计算三角形的周长.
解:(1)∵Δ=(8+k)2﹣4×8k
=(k﹣8)2,
∵(k﹣8)2≥0,
∴△≥0,
∴无论k取任何实数,方程总有实数根;
(2)∵x1+x2=8+k,x1 x2=8k,,
(x1+x2)2=x+x+2x1 x2,
∴(8+k)2=68+16k,
解得:k=±2;
(3)解方程x2﹣(8+k)x+8k=0得x1=k,x2=8,
①当腰长为5时,则k=5,
∵5+5>8,
周长=8+5+5=18;
②当底边为5时,
∴k=8,
∵5+8>8,
∴周长=5+8+8=21.
26.如图,已知Rt△ABC中,∠ACB=90°,CA=CB=4,CD⊥AB于点D,点M是线段BD上的一个动点.
(1)如图1,若点M恰好在∠BCD的角平分线上,则AM= 4 ;
(2)如图2,若点N在线段AB上,且∠MCN=45°,过点M、N分别作ME⊥CB于点E、MF⊥CA于点F.
①求证:△ACM∽△BNC;
②求AM BN的值;
③求CE CF的值.
【分析】(1)根据等腰三角形的性质得出∠ACD=∠BCD=45°,BD=AD,进而即可求得∠ACM=∠AMC=67.5°,即可求得AM=AC=4;
(2)①由∠BNC=∠A+∠ACN=45°+∠ACN=∠ACM,∠A=∠B=45°,即可证得结论;
②根据三角形相似的性质即可求得结果;
③先证得△CEM∽△CDN,△CDM∽△CFN,然后根据相似三角形的性质即可求得结果.
解:(1)如图1,∴Rt△ABC中,∠ACB=90°,CA=CB=4,
∴∠A=∠B=45°,
∵CD⊥AB于点D,
∴∠ACD=∠BCD=45°,BD=AD,
∵CE平分∠BCD,
∴∠DCM=22.5°,
∴∠ACM=67.5°,
∴∠AMC=67.5°,
∴∠ACM=∠AMC,
∴AM=AC=4,
故答案为4;
(2)①证明:∵∠MCN=45°,
∴∠ACM=45°+∠ACN,
∵∠BNC=∠A+∠ACN=45°+∠ACN,
∴∠ACM=∠BNC,
∵∠A=∠B=45°,
∴△ACM∽△BNC;
②解:∵△ACM∽△BNC,
∴,
∴AM BN=AC BC=16;
③解:Rt△ABC中,∠ACB=90°,CA=CB=4,
∴AB=4,
∵BD=AD,
∴CD=AB=2,
∵∠MCE+∠MCD=∠NCD+∠MCD=45°,
∴∠ECM=∠DCN,
∵∠CEM=∠CDN=90°,
∴△CEM∽△CDN,
∴,
同理,△CDM∽△CFN,
∴,
∴,
∴CE CF=CD2=8.
一、选择题(共12小题,满分36分,每小题3分)
1.式子成立的条件是( )
A.a=0 B.a≥3 C.a≤3 D.a=3
2.已知两个相似三角形的相似比为4:9,则这两个三角形的对应高的比为( )
A.2:3 B.4:9 C.16:81 D.9:4
3.一元二次方程x2﹣2x﹣3=0配方后可变形为( )
A.(x+1)2=4 B.(x﹣1)2=4 C.(x+1)2=16 D.(x﹣1)2=16
4.如图,直线a∥b∥c,直线m、n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=3,BC=5,DF=12,则DE的值为( )
A. B.4 C. D.
5.一块正方形的瓷砖,面积为50cm2,它的边长大约在( )
A.4cm~5cm之间 B.5cm~6cm之间
C.6cm~7cm之间 D.7cm~8cm之间
6.在Rt△ABC中,∠C=90°,cosA=,则sinA=( )
A. B. C. D.
7.下列各式计算正确的是( )
A.=﹣2 B.(+)(﹣)=3
C.=+ D.=×
8.在美丽乡村的建设中,某村加大对绿化的投资.2016年用于绿化投资50万元,2018年用于绿化投资72万元,求这两年绿化投资的年平均增长率.设这两年绿化投资的年平均增长率为x,根据题意所列方程为( )
A.50x2=72 B.50(1+x)=7
C.50(1+x)2=72 D.50(1+x)+20(1+x)2=72
9.如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;
④△ABC与△DEF的面积比为4:1.
A.1 B.2 C.3 D.4
10.若方程x2+4x+a=0无实根,化简等于( )
A.4﹣a B.a﹣4 C.﹣(a+4) D.无法确定
11.如图,O是△ABC的重心,则图中与△ABD面积相等的三角形个数为( )
A.3 B.4 C.5 D.6
12.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从点A出发沿AB以1cm/s的速度向点B运动,同时动点E从点C出发沿CA以2cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是( )
A.3s或4.8s B.3s C.4.5s D.4.5s或4.8s
二、填空题(共6小题,满分18分。每小题3分)
13.计算的结果是 .
14.点A(5,m)和点B(n,﹣3)关于原点对称,则m+n= .
15.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长是 .
16.若关于x的一元二次方程kx2﹣(k+2)x+k2+k=0有一个根为0,则k的值为 .
17.现有四张外观一样的卡片,背面朝上,正面分别有一个二次根式:、、、,从中任取一张卡片,再从剩下的卡片中又抽取一张,则两次所取卡片上的二次根式是同类二次根式的概率是 .
18.已知a是x2+x﹣2=0的根,则代数式(a2+a)(a﹣+3)的值为 .
三、解答题(共8小题,满分66分)
19.计算:(﹣1)2021+2sin60°+|﹣|﹣.
20.解方程:3x(x+2)=5(x+2)
21.如图,在 ABCD中,DE⊥AB于点E,交AC于点F,且AE:EB=1:2.
(1)求证:△AEF∽△CDF;
(2)求△AEF与△AFD的面积比.
22.用一段长为30m的篱笆围成一个靠墙的矩形菜园,墙的长度为18m.
(1)设垂直于墙的一边长为xm,则是菜园的面积为 ;
(2)若菜园的面积为100m2,求x的值.
23.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
24.如图,楼高AB为26米,从楼顶A处测得旗杆顶C的俯角为60°,又从距离楼底B处4m的一窗口E处测得旗杆顶C的仰角为45°,求旗杆CD的高.
25.已知关于x的一元二次方程x2﹣(8+k)x+8k=0.
(1)证明:无论k取任何实数,方程总有实数根.
(2)若,求k的值.
(3)若等腰三角形的一边长为5,另两边长恰好是这个方程的两个根,求这个等腰三角形的周长.
26.如图,已知Rt△ABC中,∠ACB=90°,CA=CB=4,CD⊥AB于点D,点M是线段BD上的一个动点.
(1)如图1,若点M恰好在∠BCD的角平分线上,则AM= ;
(2)如图2,若点N在线段AB上,且∠MCN=45°,过点M、N分别作ME⊥CB于点E、MF⊥CA于点F.
①求证:△ACM∽△BNC;
②求AM BN的值;
③求CE CF的值.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.式子成立的条件是( )
A.a=0 B.a≥3 C.a≤3 D.a=3
【分析】由二次根式的定义,被开方数是非负数,即可求解.
解:当a﹣3≥0时,成立,
∴a≥3,
故选:B.
2.已知两个相似三角形的相似比为4:9,则这两个三角形的对应高的比为( )
A.2:3 B.4:9 C.16:81 D.9:4
【分析】直接利用相似三角形的性质求解.
解:因为两个相似三角形的相似比为4:9,
所以则这两个三角形的对应高的比为4:9.
故选:B.
3.一元二次方程x2﹣2x﹣3=0配方后可变形为( )
A.(x+1)2=4 B.(x﹣1)2=4 C.(x+1)2=16 D.(x﹣1)2=16
【分析】根据配方法即可求出答案.
解:∵x2﹣2x﹣3=0,
∴x2﹣2x+1=4,
∴(x﹣1)2=4,
故选:B.
4.如图,直线a∥b∥c,直线m、n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=3,BC=5,DF=12,则DE的值为( )
A. B.4 C. D.
【分析】由平行线的性质得出=,即=,解方程即可得出结果.
解:∵DF=12,
∴EF=12﹣DE,
∵a∥b∥c,
∴=,
即:=,
解得:DE=,
故选:C.
5.一块正方形的瓷砖,面积为50cm2,它的边长大约在( )
A.4cm~5cm之间 B.5cm~6cm之间
C.6cm~7cm之间 D.7cm~8cm之间
【分析】根据正方形的面积公式求得:边长×边长=50,所以边长=(取正值).
解:设正方形的边长为a,则
a2=50,
∴,
∵正方形的边长a>0,
∴=,
又∵<,即7<<8,
7<a<8;
故选:D.
6.在Rt△ABC中,∠C=90°,cosA=,则sinA=( )
A. B. C. D.
【分析】根据同一锐角的正弦与余弦的平方和是1,即可求解.
解:∵sin2A+cos2A=1,即sin2A+()2=1,
∴sin2A=,
∴sinA=或﹣(舍去),
∴sinA=.
故选:C.
7.下列各式计算正确的是( )
A.=﹣2 B.(+)(﹣)=3
C.=+ D.=×
【分析】直接利用二次根式混合运算法则结合二次根式的性质分别化简得出答案.
解:A.=2,故此选项不合题意;
B.(+)(﹣)=3,故此选项符合题意;
C.=,故此选项不合题意;
D.=×,故此选项不合题意;
故选:B.
8.在美丽乡村的建设中,某村加大对绿化的投资.2016年用于绿化投资50万元,2018年用于绿化投资72万元,求这两年绿化投资的年平均增长率.设这两年绿化投资的年平均增长率为x,根据题意所列方程为( )
A.50x2=72 B.50(1+x)=7
C.50(1+x)2=72 D.50(1+x)+20(1+x)2=72
【分析】设这两年绿化投资的年平均增长率为x,根据2016年及2018年用于绿化投资的金额,即可得出关于x的一元二次方程,此题得解.
解:设这两年绿化投资的年平均增长率为x,
依题意,得:50(1+x)2=72.
故选:C.
9.如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;
④△ABC与△DEF的面积比为4:1.
A.1 B.2 C.3 D.4
【分析】根据位似图形的性质,得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出 ②△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
解:根据位似性质得出①△ABC与△DEF是位似图形,
②△ABC与△DEF是相似图形,
∵将△ABC的三边缩小的原来的,
∴△ABC与△DEF的周长比为2:1,
故③选项错误,
根据面积比等于相似比的平方,
∴④△ABC与△DEF的面积比为4:1.
故选:C.
10.若方程x2+4x+a=0无实根,化简等于( )
A.4﹣a B.a﹣4 C.﹣(a+4) D.无法确定
【分析】先根据方程无实根判断出a的取值范围,再代入原代数式计算即可.
解:∵方程x2+4x+a=0无实根,∴Δ=42﹣4a<0,∴a>4.
==|a﹣4|,
∵a>4,∴|a﹣4|=a﹣4.
故选:B.
11.如图,O是△ABC的重心,则图中与△ABD面积相等的三角形个数为( )
A.3 B.4 C.5 D.6
【分析】根据题干条件D、E、F为△ABC三边的中点,故得BD=CD,又知△ABD与△ADC的高相等,于是得到△ABD与△ACD的面积相等并且为△ABC面积的一半,同理可得△CBE与△ABE,△ACF与△BCF面积相等,并且都为△ABC面积的一半,即可求出与△ABD面积相等的三角形个数,
解:∵O是△ABC的重心,
∴BD=CD,
又∵△ABD与△ADC的高相等,
∴△ABD与△ACD的面积相等=S△ABC,
同理可知:△CBE与△ABE,△ACF与△BCF面积相等,并且都为△ABC面积的一半,
∴图中与△ABD面积相等的三角形个数为5个,
故选:C.
12.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从点A出发沿AB以1cm/s的速度向点B运动,同时动点E从点C出发沿CA以2cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是( )
A.3s或4.8s B.3s C.4.5s D.4.5s或4.8s
【分析】如果以点A、D、E为顶点的三角形与△ABC相似,由于A与A对应,那么分两种情况:①D与B对应;②D与C对应.根据相似三角形的性质分别作答.
解:如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,
则AD=t(cm),CE=2t(cm),AE=AC﹣CE=(12﹣2t)(cm),
①当D与B对应时,有△ADE∽△ABC,
∴AD:AB=AE:AC,
∴t:6=(12﹣2t):12,
∴t=3;
②当D与C对应时,有△ADE∽△ACB,
∴AD:AC=AE:AB,
∴t:12=(12﹣2t):6,
∴t=4.8,
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒,
故选:A.
二、填空题(共6小题,满分18分。每小题3分)
13.计算的结果是 2 .
【分析】直接化简二次根式进而合并得出答案.
解:原式=+
=2.
故答案为:2.
14.点A(5,m)和点B(n,﹣3)关于原点对称,则m+n= ﹣2 .
【分析】平面内关于原点对称的点的坐标特点为:横坐标、纵坐标都互为相反数,由此可求解.
解:∵点A(5,m)和点B(n,﹣3)关于原点对称,
∴m=3,n=﹣5,
∴m+n=3+(﹣5)=﹣2,
故答案为:﹣2.
15.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长是 5 .
【分析】因为四条线段成比例,可根据前两条线段,确定其比例,进而求出x的值.
解:∵m:n=2:8=1:4,
∴x:y=1:4,
∵y=20,
∴x=5.
16.若关于x的一元二次方程kx2﹣(k+2)x+k2+k=0有一个根为0,则k的值为 ﹣1 .
【分析】根据一元二次方程的解的定义得到k2+k=0,再解关于k的方程,然后根据一元二次方程的定义确定k的值.
解:把x=0代入一元二次方程kx2﹣(k+2)x+k2+k=0得k2+k=0,
解得k1=0,k2=﹣1,
而k≠0,
所以k的值为﹣1.
故答案为:﹣1.
17.现有四张外观一样的卡片,背面朝上,正面分别有一个二次根式:、、、,从中任取一张卡片,再从剩下的卡片中又抽取一张,则两次所取卡片上的二次根式是同类二次根式的概率是 .
【分析】将、、、四张卡片分别记作A、B、C、D,其中A、C是同类二次根式,B、D是同类二次根式,画树状图列出所有等可能结果,找到符合条件的结果数,根据概率公式求解即可.
解:=2,=5,=3,
将、、、四张卡片分别记作A、B、C、D,
其中A、C是同类二次根式,B、D是同类二次根式,
画树状图如下:
共有12种等可能的结果,其中两次所取卡片上的二次根式是同类二次根式的有4种结果,
所以两次所取卡片上的二次根式是同类二次根式的概率为=,
故答案为:.
18.已知a是x2+x﹣2=0的根,则代数式(a2+a)(a﹣+3)的值为 4 .
【分析】先利用一元二次方程根的定义得到a2=﹣a+2,a2+a=2,再利用通分和整体代入的方法进行计算即可.
解:∵a是x2+x﹣2=0的根,
∴a2+a﹣2=0.
∴a2﹣2=﹣a,a2+a=2.
∴(a2+a)(a﹣+3)
=2×(+3)
=2×(﹣+3)
=4.
故答案是:4.
三、解答题(共8小题,满分66分)
19.计算:(﹣1)2021+2sin60°+|﹣|﹣.
【分析】首先计算乘方、特殊角的三角函数值、开方和绝对值,然后计算乘法,最后从左向右依次计算,求出算式的值即可.
解:(﹣1)2021+2sin60°+|﹣|﹣
=﹣1+2×+﹣2
=﹣1++﹣2
=﹣1.
20.解方程:3x(x+2)=5(x+2)
【分析】本题可先对方程进行移项,然后提取公因式x+2,将原式化为两式相乘的形式,再根据“两式相乘值为0,这两式中至少有一式值为0”来解题.
解:原方程可化为
3x(x+2)﹣5(x+2)=0,
(3x﹣5)(x+2)=0,
解得x1=﹣2,.
21.如图,在 ABCD中,DE⊥AB于点E,交AC于点F,且AE:EB=1:2.
(1)求证:△AEF∽△CDF;
(2)求△AEF与△AFD的面积比.
【分析】(1)由平行四边形的性质可得CD∥AB,可得结论;
(2)由相似三角形的性质可得,即可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴△AEF∽△CDF;
(2)解:∵AE:EB=1:2,
∴AE:AB=1:3,
∴AE:CD=1:3,
∵△AEF∽△CDF,
∴,
∵S△AEF=,S△AFD=,
∴S△AEF:S△AFD=EF:DF=.
22.用一段长为30m的篱笆围成一个靠墙的矩形菜园,墙的长度为18m.
(1)设垂直于墙的一边长为xm,则是菜园的面积为 x(30﹣2x)m2 ;
(2)若菜园的面积为100m2,求x的值.
【分析】(1)设垂直于墙的一边长为xm,则平行于墙的一边长为(30﹣2x)m,利用矩形的面积计算公式,即可用含x的代数式表示出菜园的面积;
(2)根据菜园的面积为100m2,即可得出关于x的一元二次方程,解之即可得出x的值,再结合墙的长度为18m,即可确定x的值.
解:(1)设垂直于墙的一边长为xm,则平行于墙的一边长为(30﹣2x)m,
∴菜园的面积为x(30﹣2x)m2.
故答案为:x(30﹣2x)m2.
(2)依题意得:x(30﹣2x)m2=100,
整理得:x2﹣15x+50=0,
解得:x1=5,x2=10.
当x=5时,30﹣2x=30﹣2×5=20>18,不合题意,舍去;
当x=10时,30﹣2x=30﹣2×10=10<18,符合题意.
答:x的值为10.
23.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 200 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 81° ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
【分析】(1)用支付宝、现金及其他的人数和除以这三者的百分比之和可得总人数;
(2)用360°乘以“支付宝”人数所占比例即可得;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人恰好选择同一种支付方式的情况,再利用概率公式即可求得答案.
解:(1)这次活动共调查的人数为30÷15%=200(人),
故答案为:200;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为360°×=81°,
故答案为:81°;
(3)将微信记为A,支付宝记为B,银行卡记为C,列表格如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能性的结果,其中两人恰好选择同一种支付方式的结果有3种,
则P(两人恰好选择同一种支付方式)=.
24.如图,楼高AB为26米,从楼顶A处测得旗杆顶C的俯角为60°,又从距离楼底B处4m的一窗口E处测得旗杆顶C的仰角为45°,求旗杆CD的高.
【分析】首先利用图形得出BE=4m,∠FEC=45°,∠FAC=30°,则AE=22m,进而利用锐角三角函数关系求出即可.
解:过点C作CF⊥AB于点F,根据题意可得:
BE=4m,∠FEC=45°,∠FAC=30°,则AE=22m
设EF=xm,则FC=xm,AF=(22﹣x)m,
故tan30°===,
解得:x=11﹣11,
故DC=11﹣11+4=(11﹣7)m
答:旗杆CD的高为(11﹣7)m.
25.已知关于x的一元二次方程x2﹣(8+k)x+8k=0.
(1)证明:无论k取任何实数,方程总有实数根.
(2)若,求k的值.
(3)若等腰三角形的一边长为5,另两边长恰好是这个方程的两个根,求这个等腰三角形的周长.
【分析】(1)根据根的判别式即可得到结论;
(2)先计算Δ=(8+k)2﹣4×8k,整理得到Δ=(k﹣8)2,根据非负数的性质得到△≥0,然后根据△的意义即可得到结论;
(3)先解出原方程的解为x1=k,x2=8,然后分类讨论:腰长为5时,则k=5;当底边为5时,则得到k=8,然后分别计算三角形的周长.
解:(1)∵Δ=(8+k)2﹣4×8k
=(k﹣8)2,
∵(k﹣8)2≥0,
∴△≥0,
∴无论k取任何实数,方程总有实数根;
(2)∵x1+x2=8+k,x1 x2=8k,,
(x1+x2)2=x+x+2x1 x2,
∴(8+k)2=68+16k,
解得:k=±2;
(3)解方程x2﹣(8+k)x+8k=0得x1=k,x2=8,
①当腰长为5时,则k=5,
∵5+5>8,
周长=8+5+5=18;
②当底边为5时,
∴k=8,
∵5+8>8,
∴周长=5+8+8=21.
26.如图,已知Rt△ABC中,∠ACB=90°,CA=CB=4,CD⊥AB于点D,点M是线段BD上的一个动点.
(1)如图1,若点M恰好在∠BCD的角平分线上,则AM= 4 ;
(2)如图2,若点N在线段AB上,且∠MCN=45°,过点M、N分别作ME⊥CB于点E、MF⊥CA于点F.
①求证:△ACM∽△BNC;
②求AM BN的值;
③求CE CF的值.
【分析】(1)根据等腰三角形的性质得出∠ACD=∠BCD=45°,BD=AD,进而即可求得∠ACM=∠AMC=67.5°,即可求得AM=AC=4;
(2)①由∠BNC=∠A+∠ACN=45°+∠ACN=∠ACM,∠A=∠B=45°,即可证得结论;
②根据三角形相似的性质即可求得结果;
③先证得△CEM∽△CDN,△CDM∽△CFN,然后根据相似三角形的性质即可求得结果.
解:(1)如图1,∴Rt△ABC中,∠ACB=90°,CA=CB=4,
∴∠A=∠B=45°,
∵CD⊥AB于点D,
∴∠ACD=∠BCD=45°,BD=AD,
∵CE平分∠BCD,
∴∠DCM=22.5°,
∴∠ACM=67.5°,
∴∠AMC=67.5°,
∴∠ACM=∠AMC,
∴AM=AC=4,
故答案为4;
(2)①证明:∵∠MCN=45°,
∴∠ACM=45°+∠ACN,
∵∠BNC=∠A+∠ACN=45°+∠ACN,
∴∠ACM=∠BNC,
∵∠A=∠B=45°,
∴△ACM∽△BNC;
②解:∵△ACM∽△BNC,
∴,
∴AM BN=AC BC=16;
③解:Rt△ABC中,∠ACB=90°,CA=CB=4,
∴AB=4,
∵BD=AD,
∴CD=AB=2,
∵∠MCE+∠MCD=∠NCD+∠MCD=45°,
∴∠ECM=∠DCN,
∵∠CEM=∠CDN=90°,
∴△CEM∽△CDN,
∴,
同理,△CDM∽△CFN,
∴,
∴,
∴CE CF=CD2=8.
同课章节目录
