2021—2022学年人教版九年级数学下册28.1锐角三角函数课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册28.1锐角三角函数课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 11:18:00 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学下册 第二十八章 锐角三角函数
28.1 锐角三角函数 课后练习
一、选择题
1.在中,,,则的值是( )
A. B. C. D.不能确定
2.在中,、、对边分别为、、,,若,则( )
A. B. C. D.
3.⊿ABC中,∠C=90°,CD⊥AB于D,下列比值中不等于的是( )
A. B. C. D.
4.在中,,那么下列各式中不正确的是( )
A. B. C. D.
5.在中,,,,那么的值是( )
A. B. C. D.
6.⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
A.2 B. C.2 D.2
7.在 Rt 中,,如果,那么等于( )
A. B. C. D.
8.如图,在中,,则的长为( )
A.1 B.2 C.3 D.4
9.的值为( )
A.1 B.-1 C. D.
10.计算sin230°+cos260°的结果为( )
A. B. C.1 D.
二、填空题
11.已知,中,是锐角,,则的度数是__________.
12.小明沿着坡度为1∶的山坡走了100m,则他升高了______米.
13.在Rt△ABC中,∠C=90°,cosA=,AC=,则BC的长为______.
14.计算:的结果为______.
15.在中,,,则______°
三、解答题
16.计算:
(1);
(2)
17.化简求值:,其中a,b满足
18.如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,cosB=0.8,求AD的长.
19.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,.
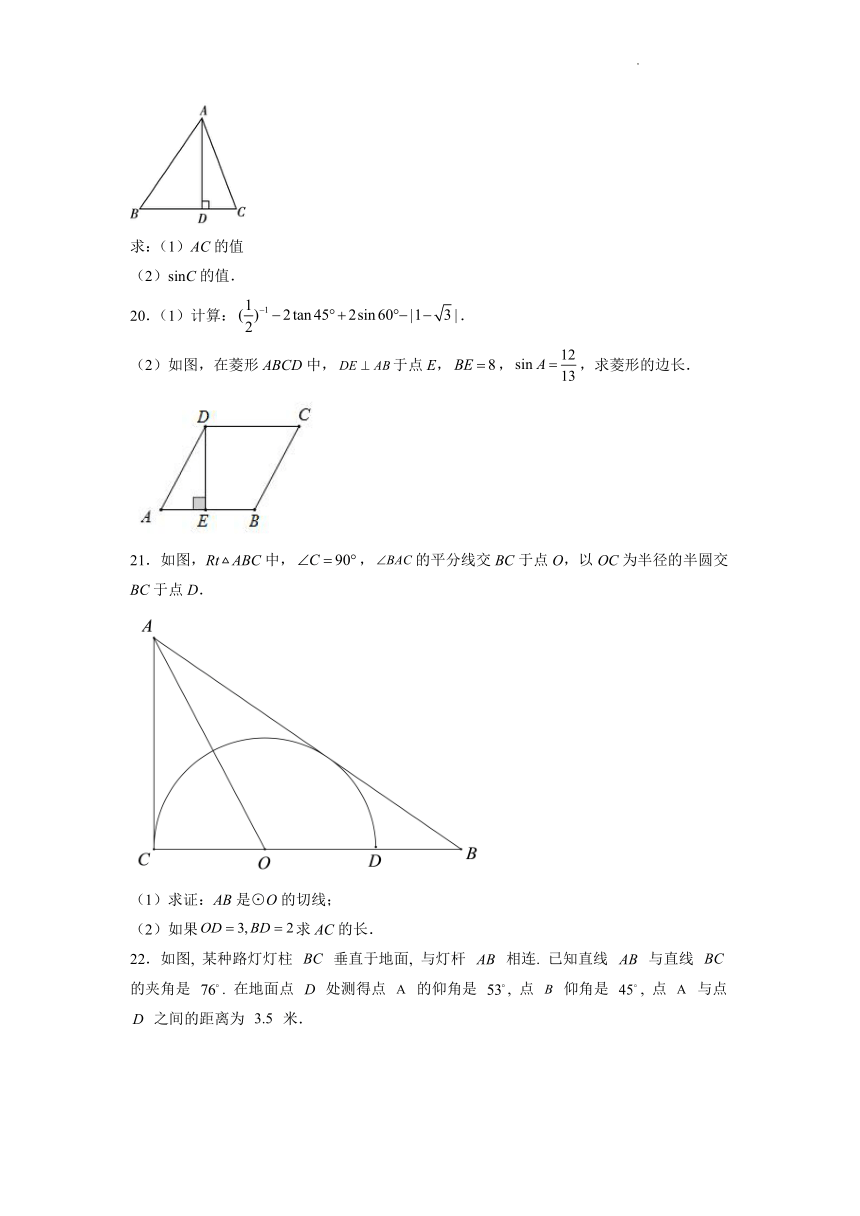
求:(1)AC的值
(2)sinC的值.
20.(1)计算:.
(2)如图,在菱形ABCD中,于点E,,,求菱形的边长.
21.如图,RtABC中,,的平分线交BC于点O,以OC为半径的半圆交BC于点D.
(1)求证:AB是⊙O的切线;
(2)如果求AC的长.
22.如图, 某种路灯灯柱 垂直于地面, 与灯杆 相连. 已知直线 与直线 的夹角是 . 在地面点 处测得点 的仰角是 , 点 仰角是 , 点 与点 之间的距离为 米.
求:(1)点 到地面的距离;
(2) 的长度.(精确到 米)
(参考数据: )
23.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且:CF是⊙O的切线.
(1)求证:∠DCF=∠CAD.
(2)探究线段CF,FD,FA的数量关系并说明理由;
(3)若cosB,AD=2,求FD的长.
【参考答案】
1.D 2.C 3.D 4.D 5.B 6.C 7.D 8.A 9.D 10.A
11.
12.50
13.1
14.
15.30
16.(1)原式
(2)原式
17.解:
,
原式
18.(1)证明:∵∠ACB=∠CAD=90°,
∴AD∥CE,
∵AE∥DC,
∴四边形AECD是平行四边形;
(2)解:∵EF⊥AB,
∴∠BFE=90°,
∵cosB==,BE=5,
∴BF=BE=×5=4,
∴EF===3,
∵AE平分∠BAC,EF⊥AB,∠ACE=90°,
∴EC=EF=3,
由(1)得:四边形AECD是平行四边形,
∴AD=EC=3.
19.(1)在中,,
∴,
∴,
∴;
(2)在中,.
20.解:(1)原式
.
(2)四边形ABCD是菱形,
.
,,
设,,
则,
,
,
∴,即菱形的边长为13.
21.(1)证明:如图,过点作,垂足为,
是的平分线,,
OC为半径
为的半径
是的切线
(2)
在中,
22.解:(1)过点A作交于点F,
则,
在中,(米),
即点A到地面的距离为2.8米;
(2)过点A作交于点H,
在四边形AFCH中,,
∴四边形AFCH是矩形,
∴,,
设BC=x,则米,
∵,,
∴,
∴,
∴(米),
∴(米),
∴米,
∵在中,,
∴,
∴
,
∴(米),
∵,
∴(米).
23.解:(1)连接OC,如图所示:
∵AD为直径,
∴,,
∵CF为的切线,
∴,即,
∵,
∴,
∴;
(2)在与中,
∵,
,
∴,
∴,
∴;
(3)∵,
∴,
在中,,
,
∴,
∴,
∴,
由(2)结论可得:,
∴,
设,则,,
将其代入结论(2)可得:
,
解得:或(舍去),
∴
28.1 锐角三角函数 课后练习
一、选择题
1.在中,,,则的值是( )
A. B. C. D.不能确定
2.在中,、、对边分别为、、,,若,则( )
A. B. C. D.
3.⊿ABC中,∠C=90°,CD⊥AB于D,下列比值中不等于的是( )
A. B. C. D.
4.在中,,那么下列各式中不正确的是( )
A. B. C. D.
5.在中,,,,那么的值是( )
A. B. C. D.
6.⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
A.2 B. C.2 D.2
7.在 Rt 中,,如果,那么等于( )
A. B. C. D.
8.如图,在中,,则的长为( )
A.1 B.2 C.3 D.4
9.的值为( )
A.1 B.-1 C. D.
10.计算sin230°+cos260°的结果为( )
A. B. C.1 D.
二、填空题
11.已知,中,是锐角,,则的度数是__________.
12.小明沿着坡度为1∶的山坡走了100m,则他升高了______米.
13.在Rt△ABC中,∠C=90°,cosA=,AC=,则BC的长为______.
14.计算:的结果为______.
15.在中,,,则______°
三、解答题
16.计算:
(1);
(2)
17.化简求值:,其中a,b满足
18.如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,cosB=0.8,求AD的长.
19.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,.
求:(1)AC的值
(2)sinC的值.
20.(1)计算:.
(2)如图,在菱形ABCD中,于点E,,,求菱形的边长.
21.如图,RtABC中,,的平分线交BC于点O,以OC为半径的半圆交BC于点D.
(1)求证:AB是⊙O的切线;
(2)如果求AC的长.
22.如图, 某种路灯灯柱 垂直于地面, 与灯杆 相连. 已知直线 与直线 的夹角是 . 在地面点 处测得点 的仰角是 , 点 仰角是 , 点 与点 之间的距离为 米.
求:(1)点 到地面的距离;
(2) 的长度.(精确到 米)
(参考数据: )
23.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且:CF是⊙O的切线.
(1)求证:∠DCF=∠CAD.
(2)探究线段CF,FD,FA的数量关系并说明理由;
(3)若cosB,AD=2,求FD的长.
【参考答案】
1.D 2.C 3.D 4.D 5.B 6.C 7.D 8.A 9.D 10.A
11.
12.50
13.1
14.
15.30
16.(1)原式
(2)原式
17.解:
,
原式
18.(1)证明:∵∠ACB=∠CAD=90°,
∴AD∥CE,
∵AE∥DC,
∴四边形AECD是平行四边形;
(2)解:∵EF⊥AB,
∴∠BFE=90°,
∵cosB==,BE=5,
∴BF=BE=×5=4,
∴EF===3,
∵AE平分∠BAC,EF⊥AB,∠ACE=90°,
∴EC=EF=3,
由(1)得:四边形AECD是平行四边形,
∴AD=EC=3.
19.(1)在中,,
∴,
∴,
∴;
(2)在中,.
20.解:(1)原式
.
(2)四边形ABCD是菱形,
.
,,
设,,
则,
,
,
∴,即菱形的边长为13.
21.(1)证明:如图,过点作,垂足为,
是的平分线,,
OC为半径
为的半径
是的切线
(2)
在中,
22.解:(1)过点A作交于点F,
则,
在中,(米),
即点A到地面的距离为2.8米;
(2)过点A作交于点H,
在四边形AFCH中,,
∴四边形AFCH是矩形,
∴,,
设BC=x,则米,
∵,,
∴,
∴,
∴(米),
∴(米),
∴米,
∵在中,,
∴,
∴
,
∴(米),
∵,
∴(米).
23.解:(1)连接OC,如图所示:
∵AD为直径,
∴,,
∵CF为的切线,
∴,即,
∵,
∴,
∴;
(2)在与中,
∵,
,
∴,
∴,
∴;
(3)∵,
∴,
在中,,
,
∴,
∴,
∴,
由(2)结论可得:,
∴,
设,则,,
将其代入结论(2)可得:
,
解得:或(舍去),
∴
