2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 11:50:51 | ||
图片预览

文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
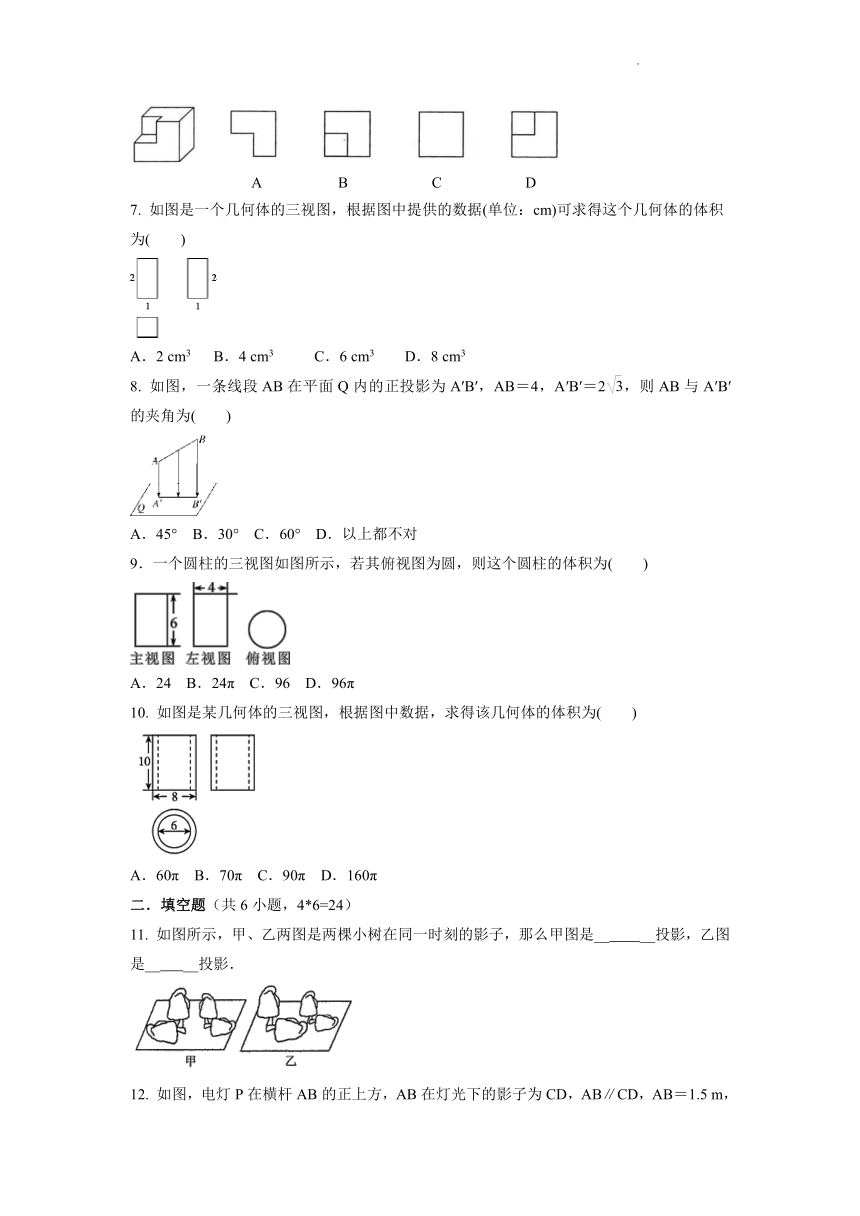
1. 如图所示的几何体的主视图是
A B C D
2. 如下摆放的几何体中,主视图与左视图有可能不同的是( )
3. 有这样一个娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好能无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )
4. 将一个小正方体按图中所示方式展开,则在展开图中表示棱a的线段是( )
A.AB B.CD C.DE D.CF
5. 如图是正方体的一种表面展开图,其中每个面上都标有一个数字.那么在原正方体中,与数字“1”相对的面上的数字是( )
A.2 B.4 C.5 D.6
6. 如图所示该几何体的俯视图是 ( )
A B C D
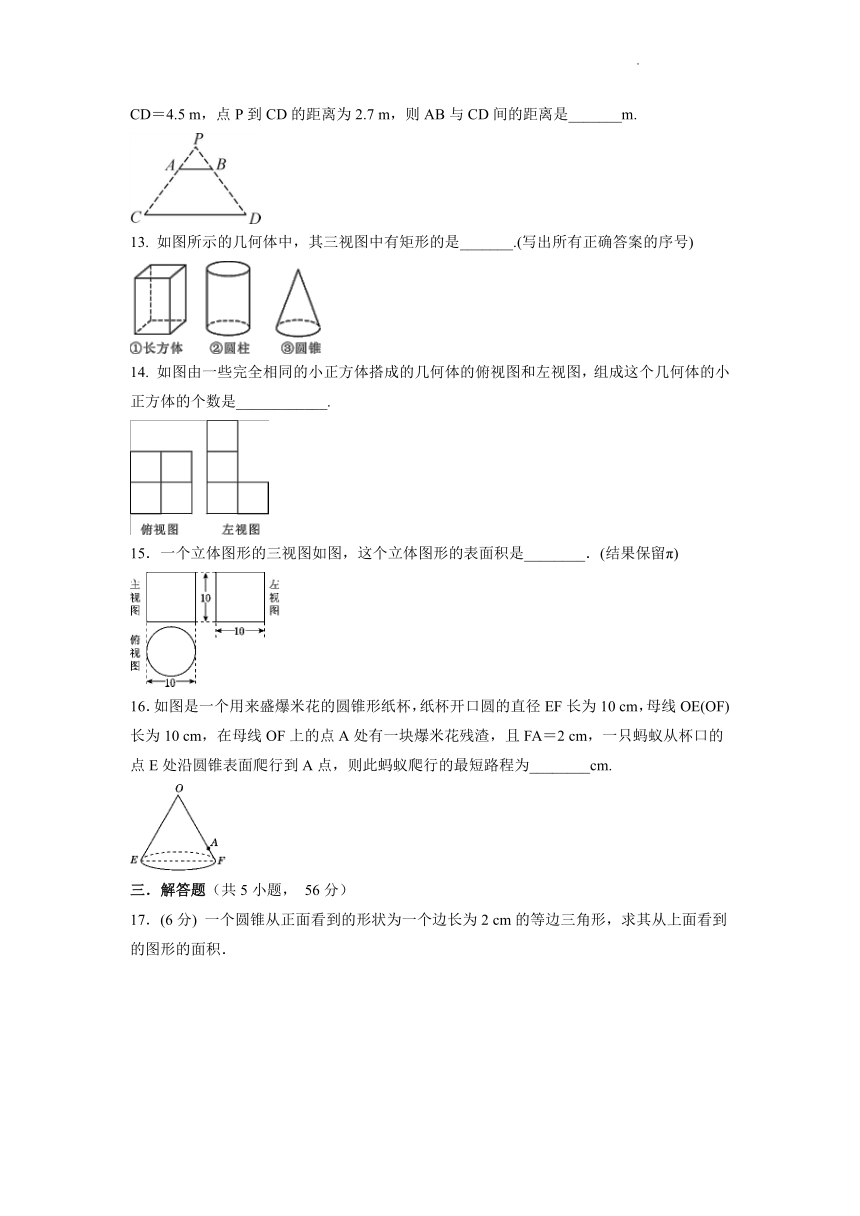
7. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )
A.2 cm3 B.4 cm3 C.6 cm3 D.8 cm3
8. 如图,一条线段AB在平面Q内的正投影为A′B′,AB=4,A′B′=2,则AB与A′B′的夹角为( )
A.45° B.30° C.60° D.以上都不对
9.一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )
A.24 B.24π C.96 D.96π
10. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
二.填空题(共6小题,4*6=24)
11. 如图所示,甲、乙两图是两棵小树在同一时刻的影子,那么甲图是__ __投影,乙图是__ __投影.
12. 如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=1.5 m,CD=4.5 m,点P到CD的距离为2.7 m,则AB与CD间的距离是_______m.
13. 如图所示的几何体中,其三视图中有矩形的是_______.(写出所有正确答案的序号)
14. 如图由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是____________.
15.一个立体图形的三视图如图,这个立体图形的表面积是________.(结果保留π)
16.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10 cm,母线OE(OF)长为10 cm,在母线OF上的点A处有一块爆米花残渣,且FA=2 cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短路程为________cm.
三.解答题(共5小题, 56分)
17.(6分) 一个圆锥从正面看到的形状为一个边长为2 cm的等边三角形,求其从上面看到的图形的面积.
18.(8分) 如图,学习小组选一名身高为1.6 m的同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量出该同学的影长为1.2 m,另一部分同学测量出同一时刻旗杆的影长为9 m,你能求出该旗杆的高度是多少米吗?
19.(8分) 某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
20.(10分) 如图,AB和DE是直立在地面上的两根立柱,AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
21.(12分) 下图是一个直三棱柱的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸,计算这个几何体的全面积.
22.(12分) 如图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形,现将宽为15 cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算裁剪的角度∠BAD的大小;
(2)计算按图③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
参考答案
1-5DDACD 6-10BABBB
11. 中心,平行
12.1.8
13.①②
14.6或7或8
15.150π
16.2
17.解:由题意得圆锥的底面圆的半径为1 cm,∴π×12=π(cm2).答:该圆锥从上面看到的图形的面积为π cm2.
18. 解:设该旗杆的高度为x m.∵在相同时刻的物高与影长成正比例,∴=,即x==12.故该旗杆的高度是12 m.
19. 由三视图可知:茶叶罐的形状为圆柱体,且茶叶罐的底面半径R为50毫米,高h为150毫米,∵每个密封罐所需钢板的面积即为圆柱体的表面积,∴S表面积=2πR2+2πRh=2π×502+2π×50×150=20000π(平方毫米),答:制作每个密封罐所需钢板的面积为20000π平方毫米.
20. 解:(1)如图,连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,∴∠ACB=∠DFE.∵∠ABC=∠DEF=90°,∴△ABC∽△DEF.∴AB∶DE=BC∶EF.∵AB=4 m,BC=3 m,EF=8 m,∴4∶DE=3∶8.∴DE= m.
21.解:(1)如图所示.
(2)由勾股定理得底面的斜边长为10cm,S底=×8×6=24(cm2),S侧=(8+6+10)×3=72(cm2),S全=72+24×2=120(cm2).答:这个几何体的全面积是120cm2.
22.解:(1)由题干中图③的包贴方法知:AB的长等于三棱柱的底面周长,∴AB=30 cm.∵纸带宽为15 cm,∴sin∠BAD=sin ∠ABM===,∴∠BAD=30°
(2)在题干图③中,将三棱柱沿过点A的侧棱剪开,得到如图①所示的侧面展开图.将图①中的△ABE向左平移30 cm,△CDF向右平移30 cm,拼成图②中的平行四边形ABCD,此平行四边形即为题干图②中的平行四边形ABCD.在图②中,由题意知:BC=BF+CF=2CF=2×=40(cm),∴所需矩形纸带的长为MB+BC=30cos30°+40=55(cm)
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如图所示的几何体的主视图是
A B C D
2. 如下摆放的几何体中,主视图与左视图有可能不同的是( )
3. 有这样一个娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好能无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )
4. 将一个小正方体按图中所示方式展开,则在展开图中表示棱a的线段是( )
A.AB B.CD C.DE D.CF
5. 如图是正方体的一种表面展开图,其中每个面上都标有一个数字.那么在原正方体中,与数字“1”相对的面上的数字是( )
A.2 B.4 C.5 D.6
6. 如图所示该几何体的俯视图是 ( )
A B C D
7. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )
A.2 cm3 B.4 cm3 C.6 cm3 D.8 cm3
8. 如图,一条线段AB在平面Q内的正投影为A′B′,AB=4,A′B′=2,则AB与A′B′的夹角为( )
A.45° B.30° C.60° D.以上都不对
9.一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )
A.24 B.24π C.96 D.96π
10. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
二.填空题(共6小题,4*6=24)
11. 如图所示,甲、乙两图是两棵小树在同一时刻的影子,那么甲图是__ __投影,乙图是__ __投影.
12. 如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=1.5 m,CD=4.5 m,点P到CD的距离为2.7 m,则AB与CD间的距离是_______m.
13. 如图所示的几何体中,其三视图中有矩形的是_______.(写出所有正确答案的序号)
14. 如图由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是____________.
15.一个立体图形的三视图如图,这个立体图形的表面积是________.(结果保留π)
16.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10 cm,母线OE(OF)长为10 cm,在母线OF上的点A处有一块爆米花残渣,且FA=2 cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短路程为________cm.
三.解答题(共5小题, 56分)
17.(6分) 一个圆锥从正面看到的形状为一个边长为2 cm的等边三角形,求其从上面看到的图形的面积.
18.(8分) 如图,学习小组选一名身高为1.6 m的同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量出该同学的影长为1.2 m,另一部分同学测量出同一时刻旗杆的影长为9 m,你能求出该旗杆的高度是多少米吗?
19.(8分) 某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
20.(10分) 如图,AB和DE是直立在地面上的两根立柱,AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
21.(12分) 下图是一个直三棱柱的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸,计算这个几何体的全面积.
22.(12分) 如图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形,现将宽为15 cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算裁剪的角度∠BAD的大小;
(2)计算按图③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
参考答案
1-5DDACD 6-10BABBB
11. 中心,平行
12.1.8
13.①②
14.6或7或8
15.150π
16.2
17.解:由题意得圆锥的底面圆的半径为1 cm,∴π×12=π(cm2).答:该圆锥从上面看到的图形的面积为π cm2.
18. 解:设该旗杆的高度为x m.∵在相同时刻的物高与影长成正比例,∴=,即x==12.故该旗杆的高度是12 m.
19. 由三视图可知:茶叶罐的形状为圆柱体,且茶叶罐的底面半径R为50毫米,高h为150毫米,∵每个密封罐所需钢板的面积即为圆柱体的表面积,∴S表面积=2πR2+2πRh=2π×502+2π×50×150=20000π(平方毫米),答:制作每个密封罐所需钢板的面积为20000π平方毫米.
20. 解:(1)如图,连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,∴∠ACB=∠DFE.∵∠ABC=∠DEF=90°,∴△ABC∽△DEF.∴AB∶DE=BC∶EF.∵AB=4 m,BC=3 m,EF=8 m,∴4∶DE=3∶8.∴DE= m.
21.解:(1)如图所示.
(2)由勾股定理得底面的斜边长为10cm,S底=×8×6=24(cm2),S侧=(8+6+10)×3=72(cm2),S全=72+24×2=120(cm2).答:这个几何体的全面积是120cm2.
22.解:(1)由题干中图③的包贴方法知:AB的长等于三棱柱的底面周长,∴AB=30 cm.∵纸带宽为15 cm,∴sin∠BAD=sin ∠ABM===,∴∠BAD=30°
(2)在题干图③中,将三棱柱沿过点A的侧棱剪开,得到如图①所示的侧面展开图.将图①中的△ABE向左平移30 cm,△CDF向右平移30 cm,拼成图②中的平行四边形ABCD,此平行四边形即为题干图②中的平行四边形ABCD.在图②中,由题意知:BC=BF+CF=2CF=2×=40(cm),∴所需矩形纸带的长为MB+BC=30cos30°+40=55(cm)
