2021-2022学年沪科版八年级下册数学第19章四边形单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版八年级下册数学第19章四边形单元测试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 11:52:57 | ||
图片预览

文档简介
2021-2022学年沪科新版八年级下册数学《第19章 四边形》单元测试卷
一.选择题(共10小题,满分30分)
1.下列结论正确的个数是( )个.
①1°=100分;②七棱柱有14个顶点;③两点之间线段最短;④各边相等的多边形是正多边形;⑤23xy是5次单项式.
A.1 B.2 C.3 D.4
2.下面图形是用木条钉成的支架,其中不容易变形的是( )
A. B. C. D.
3.下列说法不正确的是( )
A.有两组对边分别平行的四边形是平行四边形
B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等
D.平行四边形的对边平行且相等
4.如图,在△ABC中,∠ACB=90°,D是AB的中点,则下列结论不一定正确的是( )
A.CD=BD B.∠A=∠DCA
C.BD=AC D.∠B+∠ACD=90°
5.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则m、n的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
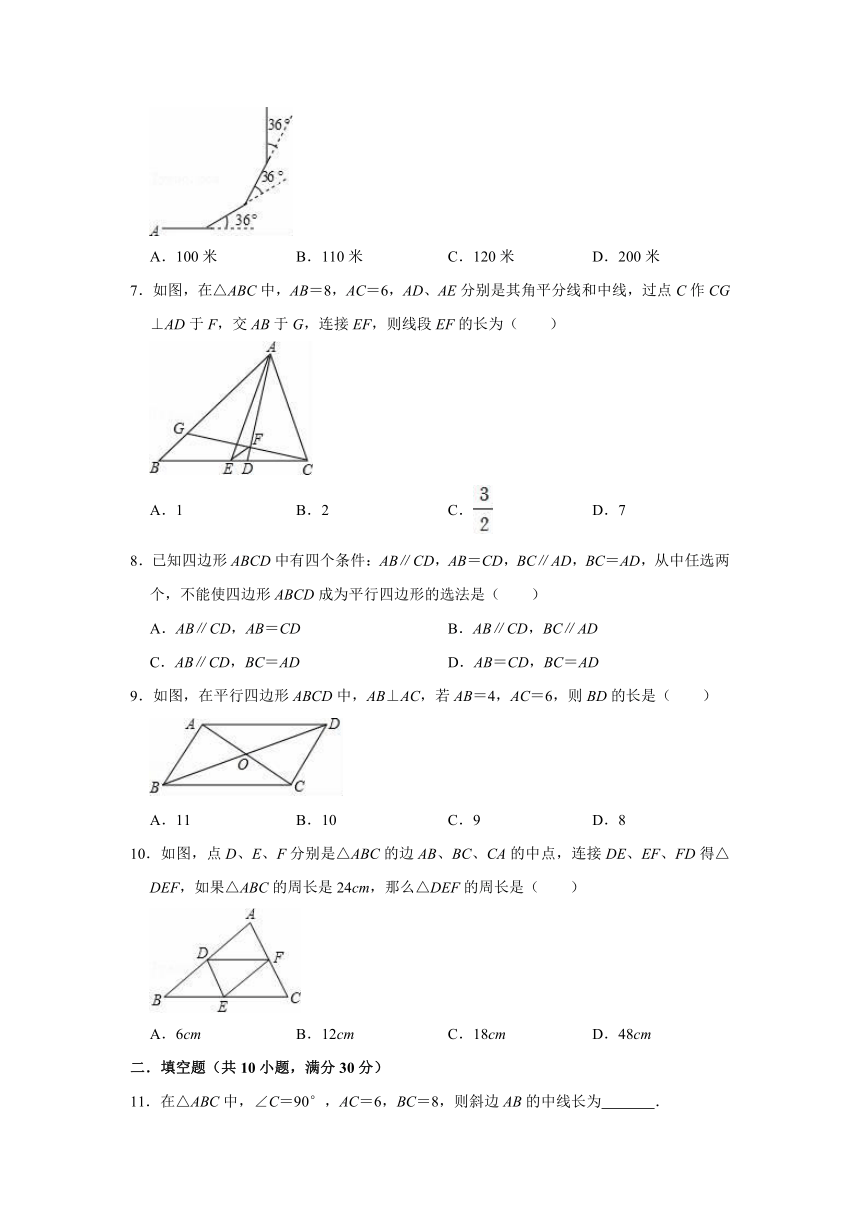
6.如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是( )
A.100米 B.110米 C.120米 D.200米
7.如图,在△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为( )
A.1 B.2 C. D.7
8.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是( )
A.AB∥CD,AB=CD B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD D.AB=CD,BC=AD
9.如图,在平行四边形ABCD中,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.11 B.10 C.9 D.8
10.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是( )
A.6cm B.12cm C.18cm D.48cm
二.填空题(共10小题,满分30分)
11.在△ABC中,∠C=90°,AC=6,BC=8,则斜边AB的中线长为 .
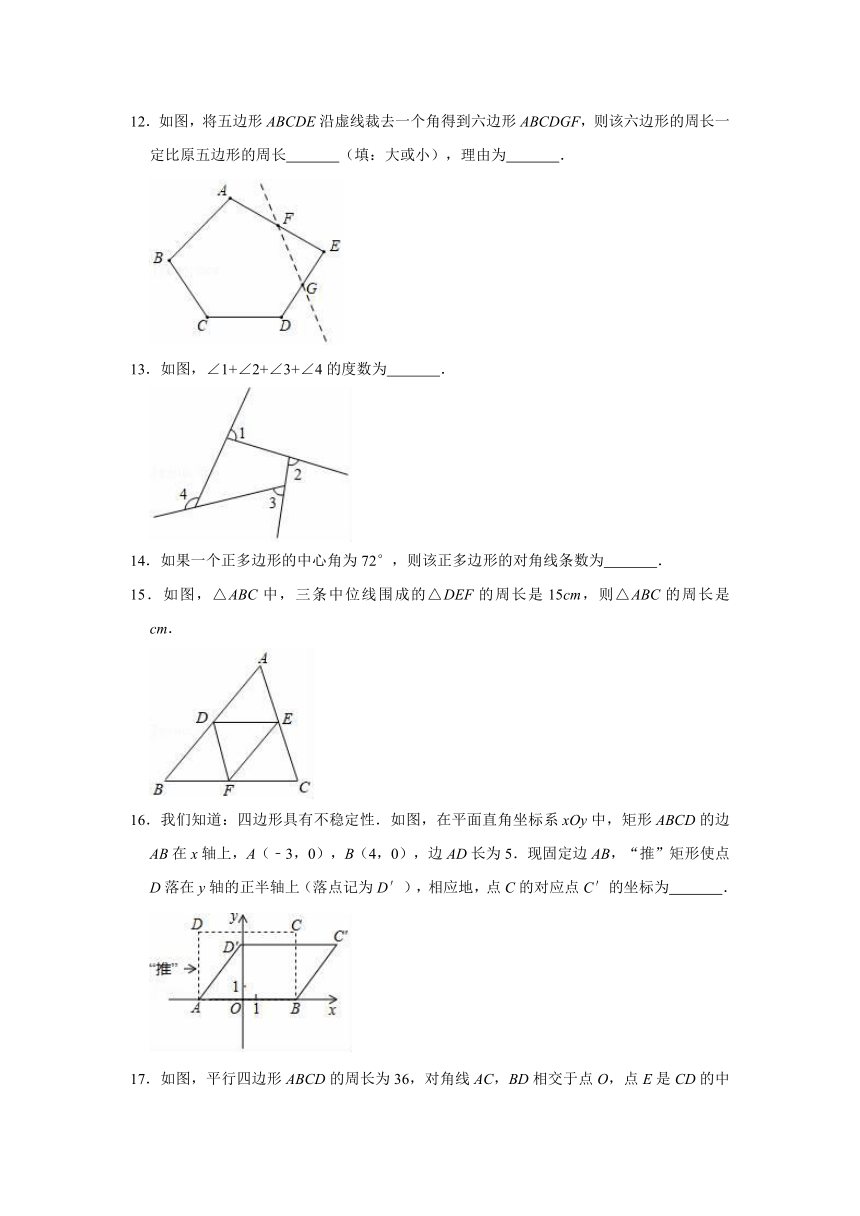
12.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
13.如图,∠1+∠2+∠3+∠4的度数为 .
14.如果一个正多边形的中心角为72°,则该正多边形的对角线条数为 .
15.如图,△ABC中,三条中位线围成的△DEF的周长是15cm,则△ABC的周长是 cm.
16.我们知道:四边形具有不稳定性.如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,A(﹣3,0),B(4,0),边AD长为5.现固定边AB,“推”矩形使点D落在y轴的正半轴上(落点记为D′),相应地,点C的对应点C′的坐标为 .
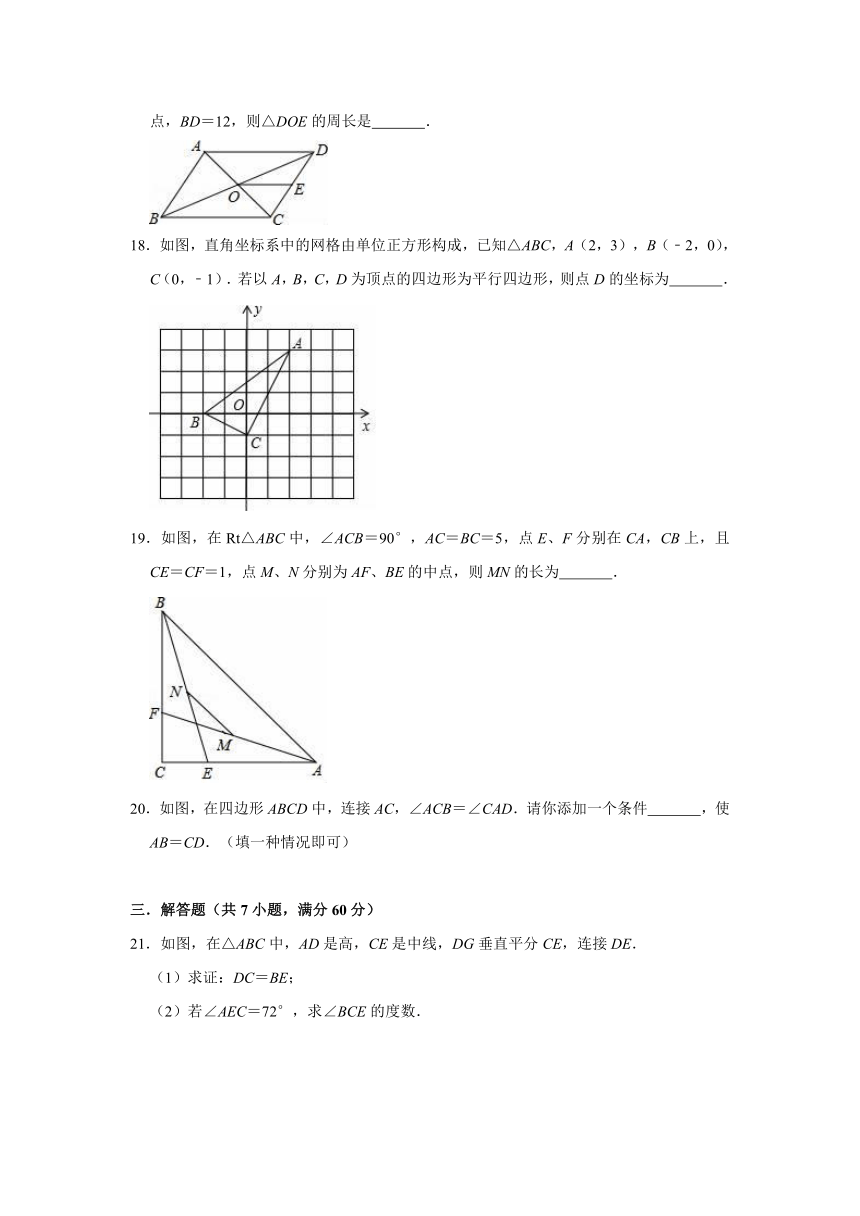
17.如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是 .
18.如图,直角坐标系中的网格由单位正方形构成,已知△ABC,A(2,3),B(﹣2,0),C(0,﹣1).若以A,B,C,D为顶点的四边形为平行四边形,则点D的坐标为 .
19.如图,在Rt△ABC中,∠ACB=90°,AC=BC=5,点E、F分别在CA,CB上,且CE=CF=1,点M、N分别为AF、BE的中点,则MN的长为 .
20.如图,在四边形ABCD中,连接AC,∠ACB=∠CAD.请你添加一个条件 ,使AB=CD.(填一种情况即可)
三.解答题(共7小题,满分60分)
21.如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.
(1)求证:DC=BE;
(2)若∠AEC=72°,求∠BCE的度数.
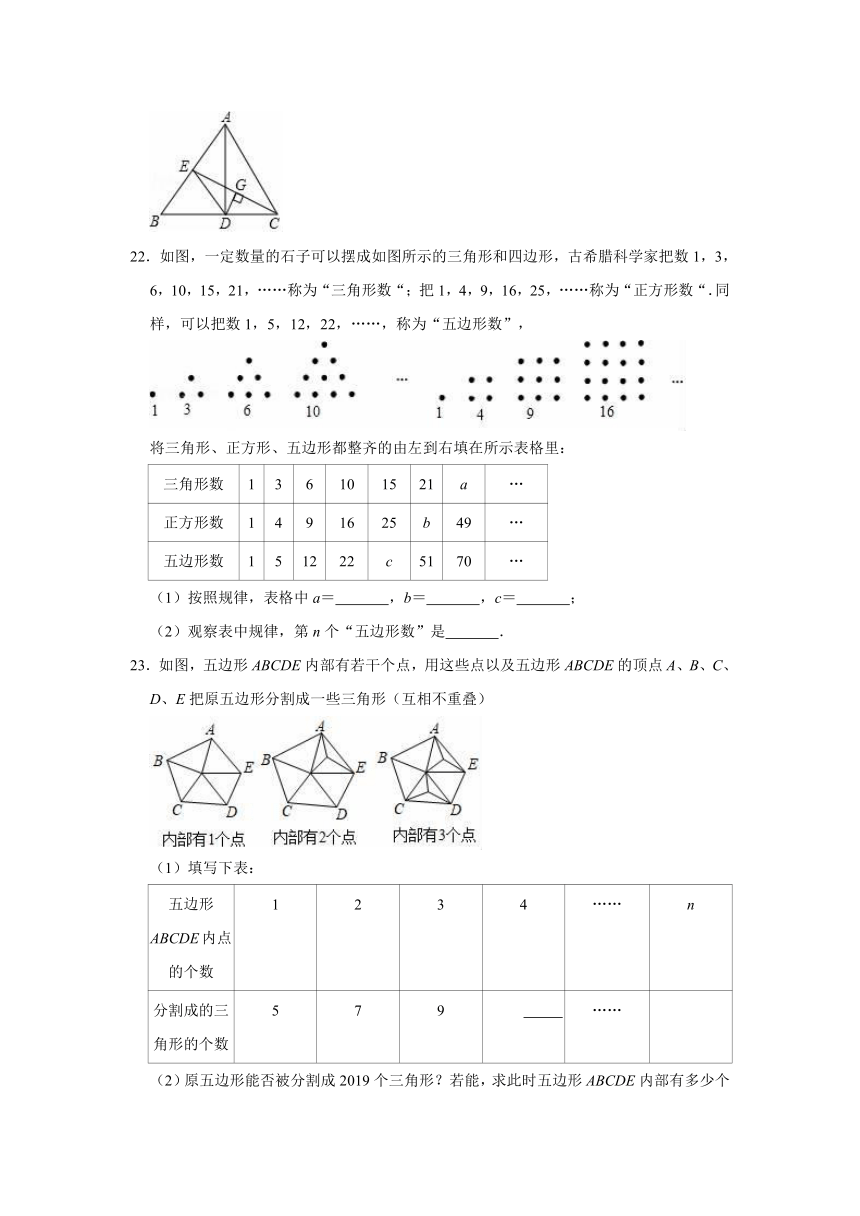
22.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 1 3 6 10 15 21 a …
正方形数 1 4 9 16 25 b 49 …
五边形数 1 5 12 22 c 51 70 …
(1)按照规律,表格中a= ,b= ,c= ;
(2)观察表中规律,第n个“五边形数”是 .
23.如图,五边形ABCDE内部有若干个点,用这些点以及五边形ABCDE的顶点A、B、C、D、E把原五边形分割成一些三角形(互相不重叠)
(1)填写下表:
五边形ABCDE内点的个数 1 2 3 4 …… n
分割成的三角形的个数 5 7 9 ……
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形ABCDE内部有多少个点?若不能,请说明理由.
24.已知n棱柱中的棱长都是12cm,且该棱柱共有12个顶点.
(1)该棱柱的底面是 边形;
(2)求该棱柱所有棱长的和及棱柱侧面展开图的面积.
25.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
26.已知:如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,EF分别交BD、AC于点G、H.求证:OG=OH.
27.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.
(1)求AE的长;
(2)若F是BC中点,求线段EF的长.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:①1°=60′,故①原说法错误;
②七棱柱有14个顶点,正确;
③两点之间线段最短,正确;
④各边、各角分别相等的多边形是正多边形,故④原说法错误;
⑤23xy是二次单项式,故⑤原说法错误;
∴正确的有:②③共2个.
故选:B.
2.解:含有三角形结构的支架不容易变形.
故选:B.
3.解:A、平行四边形的判定定理:有两组对边分别平行的四边形是平行四边形,故本选项正确;
B、平行四边形的性质:平行四边形的对角线互相平分,故本选项正确;
C、平行四边形的对角相等,邻角互补,故本选项错误;
D、平行四边形的性质:平行四边形的对边平行且相等,故本选项正确;
故选:C.
4.解:∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD,CD=AD,
∴∠A=∠DCA,
∵∠B+∠A=90°,
∴∠B+∠ACD=90°,
∴A、B、D正确;
如果BD=AC,那么△ACD是等边三角形,
必须∠A=60°,题目没有这样的条件,所以C错误;
故选:C.
5.解:对角线的数量m=6﹣3=3条;
分成的三角形的数量为n=6﹣2=4个.
故选:C.
6.解:∵每次小明都是沿直线前进10米后向左转36°,
∴他走过的图形是正多边形,
边数n=360°÷36°=10,
∴他第一次回到出发点A时,一共走了10×10=100米.
故选:A.
7.解:在△AFG和△AFC中,
,
∴△AFG≌△AFC,
∴GF=FC,AG=AC=6,
∴GB=AB﹣AG=2,
∵GF=FC,BE=EC,
∴EF=GB=1,
故选:A.
8.解:A、AB∥CD,AB=CD.根据平行四边形的判定定理“一组对边平行且相等的四边形是平行四边形”可以判定四边形ABCD是平行四边形,故本选项错误;
B、AB∥CD,BC∥AD.根据平行四边形的判定定理“两组对边分别平行的四边形是平行四边形”可以判定四边形ABCD是平行四边形,故本选项错误;
C、AB∥CD,BC=AD,根据一组对边平行,另一组对边相等,不能判定四边形ABCD是平行四边形,故本选项正确;
D、AB=CD,BC=AD,根据平行四边形的判定定理“两组对边分别相等的四边形是平行四边形”可以判定四边形ABCD是平行四边形,故本选项错误;
故选:C.
9.解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO=AC=3,
∵AB⊥AC,AB=4,
∴BO==5,
∴BD=2BO=10,
故选:B.
10.解:∵D、E分别是△ABC的边AB、BC的中点,
∴DE=AC,
同理,EF=AB,DF=BC,
∴C△DEF=DE+EF+DF=AC+BC+AB=(AC+BC+AC)=×24=12cm.
故选:B.
二.填空题(共10小题,满分30分)
11.解:∵在△ABC中,∠C=90°,AC=6,BC=8,
∴AB==10,
∴斜边AB的中线长:CD=AB=5.
故答案为:5.
12.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
13.解:∵多边形的外角和是360°,
∴∠1+∠2+∠3+∠4=360°,
故答案为:360°.
14.解:由题意可得:
边数为360°÷72°=5,
所以这个多边形的对角线条数是(条),
故答案为:5.
15.解:∵△DEF的周长是15,
∴DE+DF+EF=15,
∵DE、DF、EF分别是△ABC的中位线,
∴BC=2DE,AC=2DF,AB=2EF,
∴△ABC的周长=BC+AC+AB=2(DE+DF+EF)=30(cm),
故答案为:30.
16.解:由勾股定理,得
OD′==4,
即D′(0,4).
矩形ABCD的边AB在x轴上,
∴四边形ABC′D′是平行四边形,
AD′=BC′,C′D′=AB=4﹣(﹣3)=7,
C′与D′的纵坐标相等,
∴C′(7,4)
故答案为:(7,4).
17.解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故答案为:15.
18.解:如图,若以A,B,C,D为顶点的四边形为平行四边形,则点D的坐标为D1(0,4)或D2(4,2)或D3(﹣4,﹣4).
故答案为:(0,4)或(4,2)或(﹣4,﹣4).
19.解:取AB的中点D,连接MD、ND,如图,AE=BF=5﹣1=4,
∵点M、N分别为AF、BE的中点,
∴DM为△ABF的中位线,DN为△ABE的中位线,
∴DM=BF=2,DM∥BF,DN=AE=2,DN∥AE,
∵AE⊥BF,
∴DM⊥DN,
∴△DMN为等腰直角三角形,
∴MN=DM=2.
故答案为2.
20.解:添加的条件:AD=BC(答案不唯一).
理由是:∵∠ACB=∠CAD,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD.
故答案为:AD=BC(答案不唯一).
三.解答题(共7小题,满分60分)
21.(1)证明:∵DG垂直平分CE,
∴DE=DC,
∵AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE=AB,
∴DC=BE;
(2)∵DE=DC,
∴∠DEC=∠DCE,
∴∠EDB=∠DEC+∠BCE=2∠BCE
∵DE=BE
∴∠B=∠EDB,
∴∠B=2∠BCE,
∴∠AEC=3∠BCE=72°,
∴∠BCE=24°.
22.解:(1)∵前6个“三角形数”分别是:
1=、3=、6=、10=、15=、21=,
∴第n个“三角形数”是,
∴a==28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“五边形数”分别是:
1=,5=,12=,22=,
∴c==35.
(2)根据(1)中的规律得出:第n个“五边形数”是;
故答案为:.
23.解:(1)有1个点时,内部分割成5个三角形;
有2个点时,内部分割成5+2=7个三角形;
有3个点时,内部分割成5+2×2=9个三角形;
有4个点时,内部分割成5+2×3=11个三角形; …
以此类推,有n个点时,内部分割成5+2×(n﹣1)=(2n+3)个三角形;
故答案为:11;
(2)能.理由如下:由(1)知2n+3=2019,解得n=1008,
∴此时五边形ABCDE内部有1008点.
24.解:(1)∵棱柱共有12个顶点,
∴该棱柱是六棱柱,
故答案为:六;
(2)该棱柱所有棱长的和为:12×6×3=216(cm),
1棱柱侧面展开图12×12×6=864(cm2).
25.解:设这个多边形的边数为n,根据题意,得
(n﹣2) 180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
26.解:取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=BD,
同理:ME∥AC,ME=AC,
∵AC=BD
∴ME=MF
∴∠MEF=∠MFE,
∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG
∴OG=OH.
27.解:(1)∵AC=23,CD=10,
∴AD=23﹣10=13,
∵AB=13,
∴AB=CD,
∵AE平分∠BAC,
∴DE=BE,AE⊥BD,
∵BD=10,
∴DE=5,
∴AE===12;
(2)∵E是BD的中点,F是BC中点,
∴EF=CD==5.
一.选择题(共10小题,满分30分)
1.下列结论正确的个数是( )个.
①1°=100分;②七棱柱有14个顶点;③两点之间线段最短;④各边相等的多边形是正多边形;⑤23xy是5次单项式.
A.1 B.2 C.3 D.4
2.下面图形是用木条钉成的支架,其中不容易变形的是( )
A. B. C. D.
3.下列说法不正确的是( )
A.有两组对边分别平行的四边形是平行四边形
B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等
D.平行四边形的对边平行且相等
4.如图,在△ABC中,∠ACB=90°,D是AB的中点,则下列结论不一定正确的是( )
A.CD=BD B.∠A=∠DCA
C.BD=AC D.∠B+∠ACD=90°
5.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则m、n的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
6.如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是( )
A.100米 B.110米 C.120米 D.200米
7.如图,在△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为( )
A.1 B.2 C. D.7
8.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是( )
A.AB∥CD,AB=CD B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD D.AB=CD,BC=AD
9.如图,在平行四边形ABCD中,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.11 B.10 C.9 D.8
10.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是( )
A.6cm B.12cm C.18cm D.48cm
二.填空题(共10小题,满分30分)
11.在△ABC中,∠C=90°,AC=6,BC=8,则斜边AB的中线长为 .
12.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
13.如图,∠1+∠2+∠3+∠4的度数为 .
14.如果一个正多边形的中心角为72°,则该正多边形的对角线条数为 .
15.如图,△ABC中,三条中位线围成的△DEF的周长是15cm,则△ABC的周长是 cm.
16.我们知道:四边形具有不稳定性.如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,A(﹣3,0),B(4,0),边AD长为5.现固定边AB,“推”矩形使点D落在y轴的正半轴上(落点记为D′),相应地,点C的对应点C′的坐标为 .
17.如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是 .
18.如图,直角坐标系中的网格由单位正方形构成,已知△ABC,A(2,3),B(﹣2,0),C(0,﹣1).若以A,B,C,D为顶点的四边形为平行四边形,则点D的坐标为 .
19.如图,在Rt△ABC中,∠ACB=90°,AC=BC=5,点E、F分别在CA,CB上,且CE=CF=1,点M、N分别为AF、BE的中点,则MN的长为 .
20.如图,在四边形ABCD中,连接AC,∠ACB=∠CAD.请你添加一个条件 ,使AB=CD.(填一种情况即可)
三.解答题(共7小题,满分60分)
21.如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.
(1)求证:DC=BE;
(2)若∠AEC=72°,求∠BCE的度数.
22.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 1 3 6 10 15 21 a …
正方形数 1 4 9 16 25 b 49 …
五边形数 1 5 12 22 c 51 70 …
(1)按照规律,表格中a= ,b= ,c= ;
(2)观察表中规律,第n个“五边形数”是 .
23.如图,五边形ABCDE内部有若干个点,用这些点以及五边形ABCDE的顶点A、B、C、D、E把原五边形分割成一些三角形(互相不重叠)
(1)填写下表:
五边形ABCDE内点的个数 1 2 3 4 …… n
分割成的三角形的个数 5 7 9 ……
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形ABCDE内部有多少个点?若不能,请说明理由.
24.已知n棱柱中的棱长都是12cm,且该棱柱共有12个顶点.
(1)该棱柱的底面是 边形;
(2)求该棱柱所有棱长的和及棱柱侧面展开图的面积.
25.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
26.已知:如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,EF分别交BD、AC于点G、H.求证:OG=OH.
27.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.
(1)求AE的长;
(2)若F是BC中点,求线段EF的长.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:①1°=60′,故①原说法错误;
②七棱柱有14个顶点,正确;
③两点之间线段最短,正确;
④各边、各角分别相等的多边形是正多边形,故④原说法错误;
⑤23xy是二次单项式,故⑤原说法错误;
∴正确的有:②③共2个.
故选:B.
2.解:含有三角形结构的支架不容易变形.
故选:B.
3.解:A、平行四边形的判定定理:有两组对边分别平行的四边形是平行四边形,故本选项正确;
B、平行四边形的性质:平行四边形的对角线互相平分,故本选项正确;
C、平行四边形的对角相等,邻角互补,故本选项错误;
D、平行四边形的性质:平行四边形的对边平行且相等,故本选项正确;
故选:C.
4.解:∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD,CD=AD,
∴∠A=∠DCA,
∵∠B+∠A=90°,
∴∠B+∠ACD=90°,
∴A、B、D正确;
如果BD=AC,那么△ACD是等边三角形,
必须∠A=60°,题目没有这样的条件,所以C错误;
故选:C.
5.解:对角线的数量m=6﹣3=3条;
分成的三角形的数量为n=6﹣2=4个.
故选:C.
6.解:∵每次小明都是沿直线前进10米后向左转36°,
∴他走过的图形是正多边形,
边数n=360°÷36°=10,
∴他第一次回到出发点A时,一共走了10×10=100米.
故选:A.
7.解:在△AFG和△AFC中,
,
∴△AFG≌△AFC,
∴GF=FC,AG=AC=6,
∴GB=AB﹣AG=2,
∵GF=FC,BE=EC,
∴EF=GB=1,
故选:A.
8.解:A、AB∥CD,AB=CD.根据平行四边形的判定定理“一组对边平行且相等的四边形是平行四边形”可以判定四边形ABCD是平行四边形,故本选项错误;
B、AB∥CD,BC∥AD.根据平行四边形的判定定理“两组对边分别平行的四边形是平行四边形”可以判定四边形ABCD是平行四边形,故本选项错误;
C、AB∥CD,BC=AD,根据一组对边平行,另一组对边相等,不能判定四边形ABCD是平行四边形,故本选项正确;
D、AB=CD,BC=AD,根据平行四边形的判定定理“两组对边分别相等的四边形是平行四边形”可以判定四边形ABCD是平行四边形,故本选项错误;
故选:C.
9.解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO=AC=3,
∵AB⊥AC,AB=4,
∴BO==5,
∴BD=2BO=10,
故选:B.
10.解:∵D、E分别是△ABC的边AB、BC的中点,
∴DE=AC,
同理,EF=AB,DF=BC,
∴C△DEF=DE+EF+DF=AC+BC+AB=(AC+BC+AC)=×24=12cm.
故选:B.
二.填空题(共10小题,满分30分)
11.解:∵在△ABC中,∠C=90°,AC=6,BC=8,
∴AB==10,
∴斜边AB的中线长:CD=AB=5.
故答案为:5.
12.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
13.解:∵多边形的外角和是360°,
∴∠1+∠2+∠3+∠4=360°,
故答案为:360°.
14.解:由题意可得:
边数为360°÷72°=5,
所以这个多边形的对角线条数是(条),
故答案为:5.
15.解:∵△DEF的周长是15,
∴DE+DF+EF=15,
∵DE、DF、EF分别是△ABC的中位线,
∴BC=2DE,AC=2DF,AB=2EF,
∴△ABC的周长=BC+AC+AB=2(DE+DF+EF)=30(cm),
故答案为:30.
16.解:由勾股定理,得
OD′==4,
即D′(0,4).
矩形ABCD的边AB在x轴上,
∴四边形ABC′D′是平行四边形,
AD′=BC′,C′D′=AB=4﹣(﹣3)=7,
C′与D′的纵坐标相等,
∴C′(7,4)
故答案为:(7,4).
17.解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故答案为:15.
18.解:如图,若以A,B,C,D为顶点的四边形为平行四边形,则点D的坐标为D1(0,4)或D2(4,2)或D3(﹣4,﹣4).
故答案为:(0,4)或(4,2)或(﹣4,﹣4).
19.解:取AB的中点D,连接MD、ND,如图,AE=BF=5﹣1=4,
∵点M、N分别为AF、BE的中点,
∴DM为△ABF的中位线,DN为△ABE的中位线,
∴DM=BF=2,DM∥BF,DN=AE=2,DN∥AE,
∵AE⊥BF,
∴DM⊥DN,
∴△DMN为等腰直角三角形,
∴MN=DM=2.
故答案为2.
20.解:添加的条件:AD=BC(答案不唯一).
理由是:∵∠ACB=∠CAD,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD.
故答案为:AD=BC(答案不唯一).
三.解答题(共7小题,满分60分)
21.(1)证明:∵DG垂直平分CE,
∴DE=DC,
∵AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE=AB,
∴DC=BE;
(2)∵DE=DC,
∴∠DEC=∠DCE,
∴∠EDB=∠DEC+∠BCE=2∠BCE
∵DE=BE
∴∠B=∠EDB,
∴∠B=2∠BCE,
∴∠AEC=3∠BCE=72°,
∴∠BCE=24°.
22.解:(1)∵前6个“三角形数”分别是:
1=、3=、6=、10=、15=、21=,
∴第n个“三角形数”是,
∴a==28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“五边形数”分别是:
1=,5=,12=,22=,
∴c==35.
(2)根据(1)中的规律得出:第n个“五边形数”是;
故答案为:.
23.解:(1)有1个点时,内部分割成5个三角形;
有2个点时,内部分割成5+2=7个三角形;
有3个点时,内部分割成5+2×2=9个三角形;
有4个点时,内部分割成5+2×3=11个三角形; …
以此类推,有n个点时,内部分割成5+2×(n﹣1)=(2n+3)个三角形;
故答案为:11;
(2)能.理由如下:由(1)知2n+3=2019,解得n=1008,
∴此时五边形ABCDE内部有1008点.
24.解:(1)∵棱柱共有12个顶点,
∴该棱柱是六棱柱,
故答案为:六;
(2)该棱柱所有棱长的和为:12×6×3=216(cm),
1棱柱侧面展开图12×12×6=864(cm2).
25.解:设这个多边形的边数为n,根据题意,得
(n﹣2) 180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
26.解:取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=BD,
同理:ME∥AC,ME=AC,
∵AC=BD
∴ME=MF
∴∠MEF=∠MFE,
∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG
∴OG=OH.
27.解:(1)∵AC=23,CD=10,
∴AD=23﹣10=13,
∵AB=13,
∴AB=CD,
∵AE平分∠BAC,
∴DE=BE,AE⊥BD,
∵BD=10,
∴DE=5,
∴AE===12;
(2)∵E是BD的中点,F是BC中点,
∴EF=CD==5.
