28.2.1 解直角三角形 同步练习(含答案)
文档属性
| 名称 | 28.2.1 解直角三角形 同步练习(含答案) | 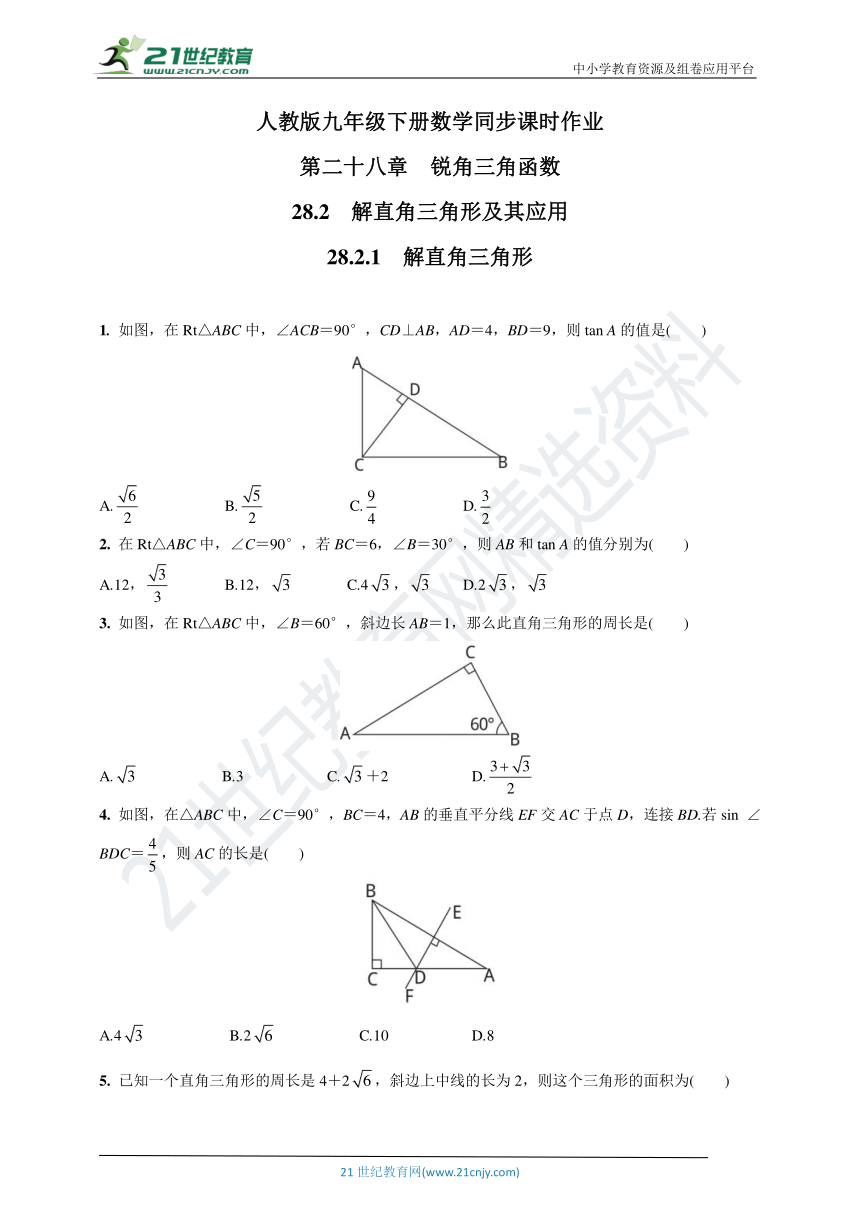 | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 12:53:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AD=4,BD=9,则tan A的值是( )
A. B. C. D.
2. 在Rt△ABC中,∠C=90°,若BC=6,∠B=30°,则AB和tan A的值分别为( )
A.12, B.12, C.4, D.2,
3. 如图,在Rt△ABC中,∠B=60°,斜边长AB=1,那么此直角三角形的周长是( )
A. B.3 C.+2 D.
4. 如图,在△ABC中,∠C=90°,BC=4,AB的垂直平分线EF交AC于点D,连接BD.若sin ∠BDC=,则AC的长是( )
A.4 B.2 C.10 D.8
5. 已知一个直角三角形的周长是4+2,斜边上中线的长为2,则这个三角形的面积为( )
A.5 B.2 C. D.1
6. 已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C=90°,∠A=30°,斜边上的高为1,则Rt△ABC三边的长分别为( )
A.a=,b=2,c= B.a=,b=2,c=
C.a=2,b=,c= D.a=2,b=2,c=4
7. 在Rt△ABC中,∠C=90°,∠A=30°,若斜边上中线的长为1,则斜边上的高为( )
A. B. C. D.
8. 一个三角形的一边长是2m,这边上的中线长为m,另两边之和为m+m,则这个三角形的面积是( )
A.m2 B.m2 C.m2 D.3m2
9. 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=7,c=7,则b= ,∠A= ,∠B= .
10. 如图所示,在边长相同的小正方形组成的网格中,AB与CD交于点P,那么tan ∠APD= .
11. 在△ABC中,∠C=90°,tan A=,△ABC的周长为60,那么△ABC的面积为 .
12. 在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=45°,c=14.
(2)a=,∠A=60°.
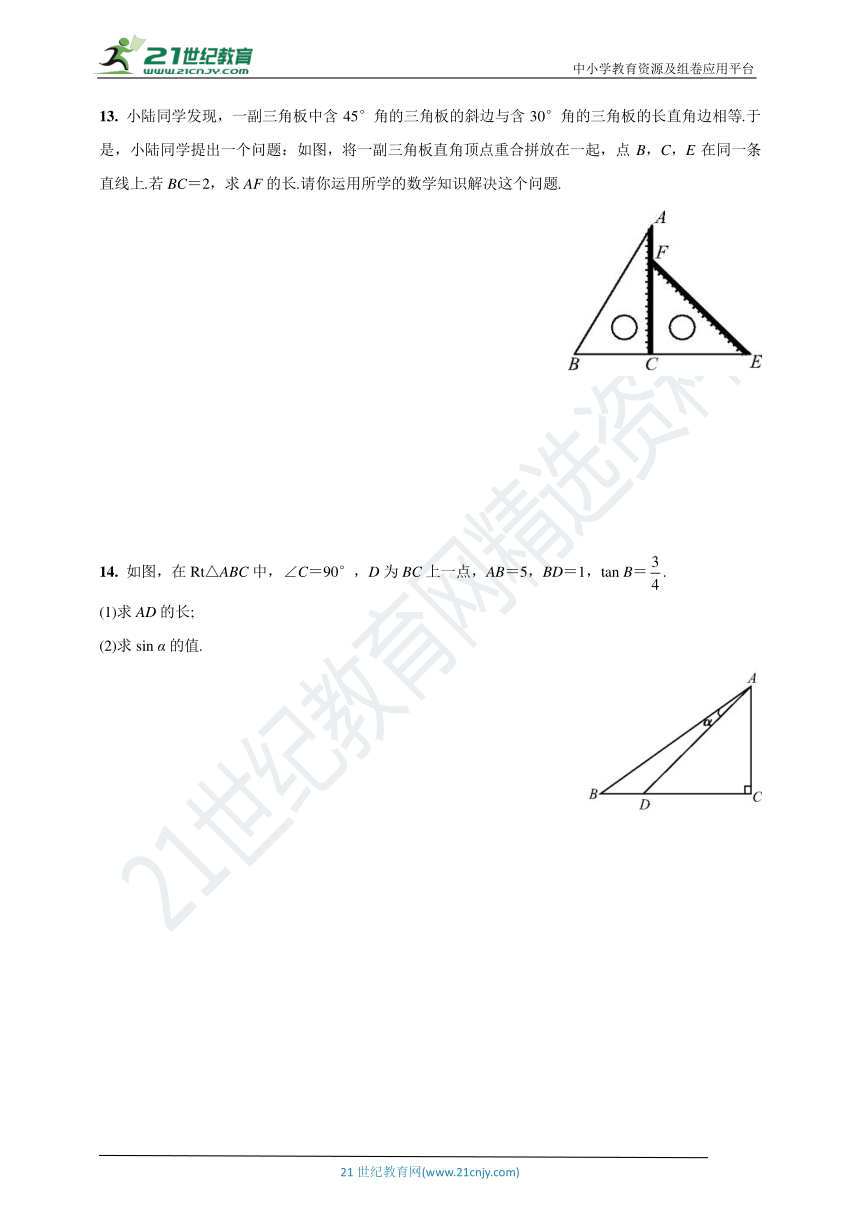
13. 小陆同学发现,一副三角板中含45°角的三角板的斜边与含30°角的三角板的长直角边相等.于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一条直线上.若BC=2,求AF的长.请你运用所学的数学知识解决这个问题.
14. 如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan B=.
(1)求AD的长;
(2)求sin α的值.
15. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan ∠ACE的值;
(2)求AE∶EB的值.
参 考 答 案
1. D 2. C 3. D 4. D 5. B 6. A 7. D 8. B
9. 7 45° 45°
10. 2
11. 120
12. 解:(1)∠A=45°,a=b==7.
(2)∠B=30°,b=,c=2.
13. 解:在Rt△ABC中,BC=2,∠A=30°,∴AC==2,∴EF=AC=2.∵∠E=45°,∴FC=EF·sin E=,∴AF=AC-FC=2-.
14. 解:(1)由tan B=可设AC=3x,BC=4x.又AC2+BC2=AB2,∴(3x)2+(4x)2=52,解得x=-1(舍去),或x=1,∴AC=3,BC=4. ∵BD=1,∴CD=3,∴AD==3.
(3)过点D作DE⊥AB于点E,∵BD·AC=AB·DE,∴DE==,∴sin α==.
15. 解:(1)由∠ACB=90°,CE⊥BD,得∠ACE=∠CBD.在△BCD中,BC=3,CD=AC=2,∠BCD=90°,∴tan ∠CBD=,即tan ∠ACE=.
(2)过点A作AC的垂线交CE的延长线于点P,则在△CAP中,CA=4,∠CAP=90°,tan ∠ACP=,∴AP=4×=.又∵∠ACB=90°,∠CAP=90°,∴BC∥AP,∴AE∶EB=AP∶BC=8∶9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AD=4,BD=9,则tan A的值是( )
A. B. C. D.
2. 在Rt△ABC中,∠C=90°,若BC=6,∠B=30°,则AB和tan A的值分别为( )
A.12, B.12, C.4, D.2,
3. 如图,在Rt△ABC中,∠B=60°,斜边长AB=1,那么此直角三角形的周长是( )
A. B.3 C.+2 D.
4. 如图,在△ABC中,∠C=90°,BC=4,AB的垂直平分线EF交AC于点D,连接BD.若sin ∠BDC=,则AC的长是( )
A.4 B.2 C.10 D.8
5. 已知一个直角三角形的周长是4+2,斜边上中线的长为2,则这个三角形的面积为( )
A.5 B.2 C. D.1
6. 已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C=90°,∠A=30°,斜边上的高为1,则Rt△ABC三边的长分别为( )
A.a=,b=2,c= B.a=,b=2,c=
C.a=2,b=,c= D.a=2,b=2,c=4
7. 在Rt△ABC中,∠C=90°,∠A=30°,若斜边上中线的长为1,则斜边上的高为( )
A. B. C. D.
8. 一个三角形的一边长是2m,这边上的中线长为m,另两边之和为m+m,则这个三角形的面积是( )
A.m2 B.m2 C.m2 D.3m2
9. 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=7,c=7,则b= ,∠A= ,∠B= .
10. 如图所示,在边长相同的小正方形组成的网格中,AB与CD交于点P,那么tan ∠APD= .
11. 在△ABC中,∠C=90°,tan A=,△ABC的周长为60,那么△ABC的面积为 .
12. 在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=45°,c=14.
(2)a=,∠A=60°.
13. 小陆同学发现,一副三角板中含45°角的三角板的斜边与含30°角的三角板的长直角边相等.于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一条直线上.若BC=2,求AF的长.请你运用所学的数学知识解决这个问题.
14. 如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan B=.
(1)求AD的长;
(2)求sin α的值.
15. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan ∠ACE的值;
(2)求AE∶EB的值.
参 考 答 案
1. D 2. C 3. D 4. D 5. B 6. A 7. D 8. B
9. 7 45° 45°
10. 2
11. 120
12. 解:(1)∠A=45°,a=b==7.
(2)∠B=30°,b=,c=2.
13. 解:在Rt△ABC中,BC=2,∠A=30°,∴AC==2,∴EF=AC=2.∵∠E=45°,∴FC=EF·sin E=,∴AF=AC-FC=2-.
14. 解:(1)由tan B=可设AC=3x,BC=4x.又AC2+BC2=AB2,∴(3x)2+(4x)2=52,解得x=-1(舍去),或x=1,∴AC=3,BC=4. ∵BD=1,∴CD=3,∴AD==3.
(3)过点D作DE⊥AB于点E,∵BD·AC=AB·DE,∴DE==,∴sin α==.
15. 解:(1)由∠ACB=90°,CE⊥BD,得∠ACE=∠CBD.在△BCD中,BC=3,CD=AC=2,∠BCD=90°,∴tan ∠CBD=,即tan ∠ACE=.
(2)过点A作AC的垂线交CE的延长线于点P,则在△CAP中,CA=4,∠CAP=90°,tan ∠ACP=,∴AP=4×=.又∵∠ACB=90°,∠CAP=90°,∴BC∥AP,∴AE∶EB=AP∶BC=8∶9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
