人教版七年级数学下册 第五章相交线与平行线 小结课件(共24张)
文档属性
| 名称 | 人教版七年级数学下册 第五章相交线与平行线 小结课件(共24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
学习目标:
1.对本小节所学知识进行回顾与思考,把本节内容条理化,系统化.
2.通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言的运用.
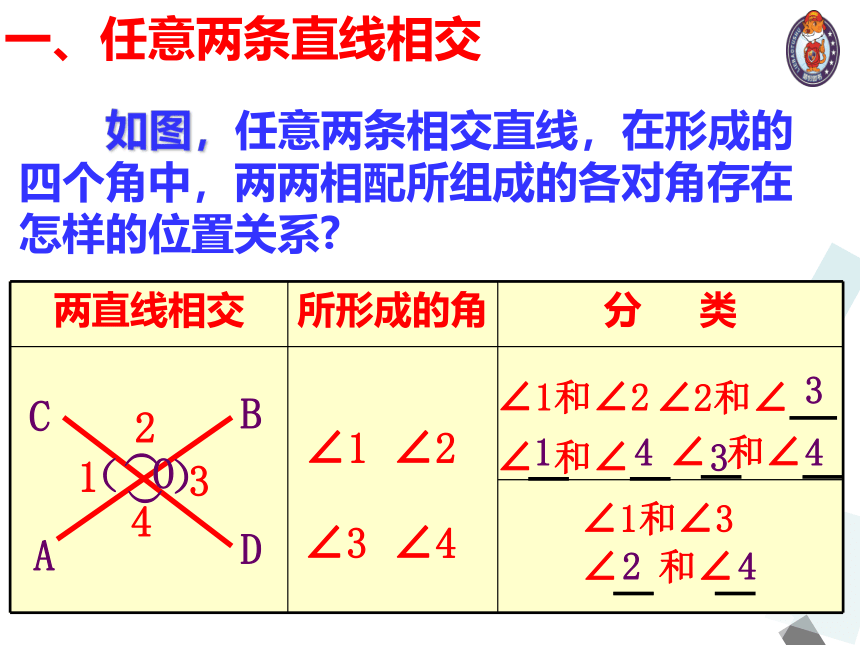
如图,任意两条相交直线,在形成的四个角中,两两相配所组成的各对角存在怎样的位置关系
两直线相交 所形成的角 分 类
O
A
B
C
D
)
(
1
3
4
2
)
(
∠3
∠1
∠2
∠4
∠1和∠2
4
∠2和∠
∠ 和∠
∠ 和∠
1
4
3
4
3
∠1和∠3
∠ 和∠
2
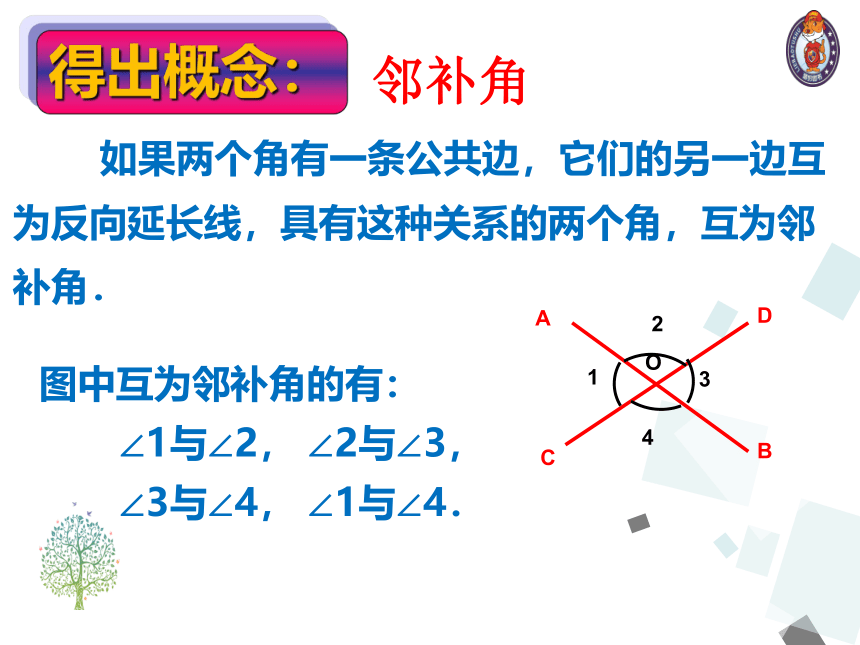
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
图中互为邻补角的有:
∠1与∠2, ∠2与∠3,
∠3与∠4, ∠1与∠4.
得出概念:
邻补角
O
C
D
A
B
1
3
4
2
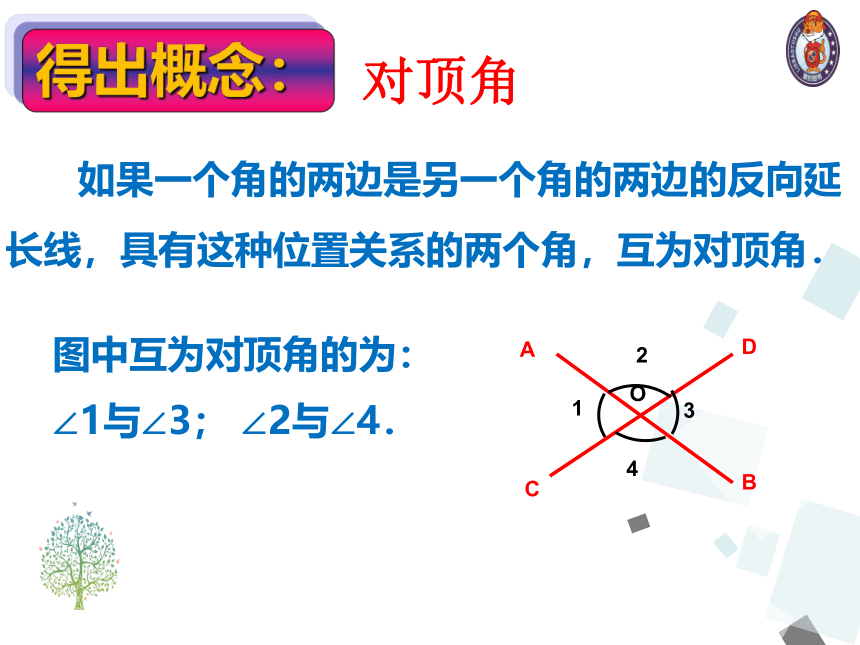
如果一个角的两边是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中互为对顶角的为:
∠1与∠3; ∠2与∠4.
对顶角
O
C
D
A
B
1
3
4
2
得出概念:
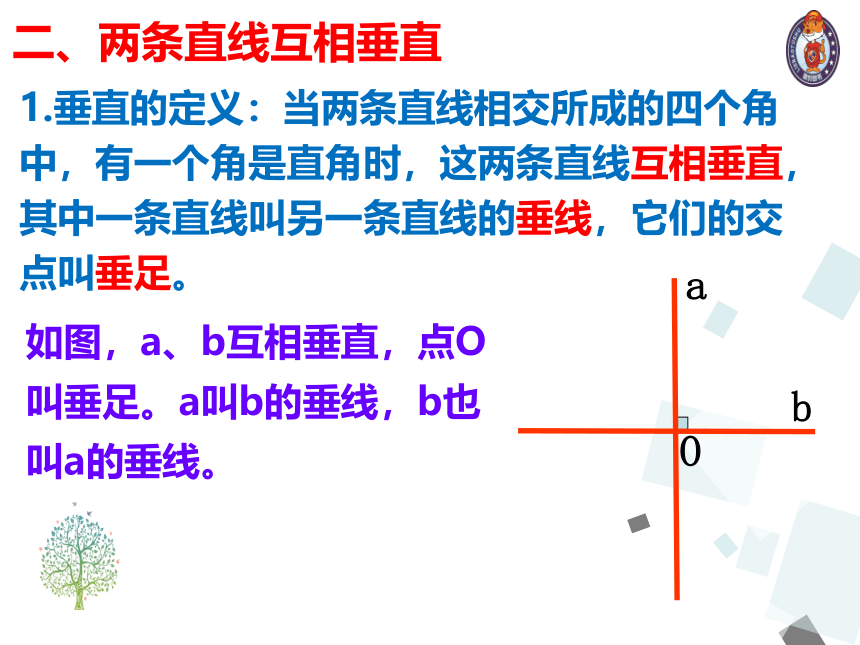
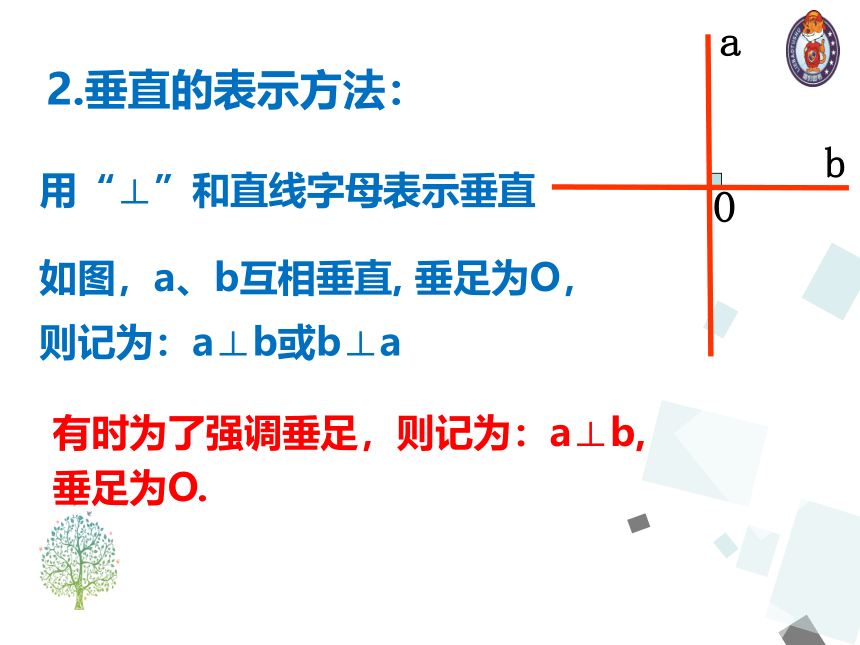
1.垂直的定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
如图,a、b互相垂直,点O叫垂足。a叫b的垂线,b也叫a的垂线。
b
a
O
二、两条直线互相垂直
用“⊥”和直线字母表示垂直
2.垂直的表示方法:
如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a
有时为了强调垂足,则记为:a⊥b, 垂足为O.
b
a
O
7
8
5
6
A
B
4
1
3
2
C
D
E
F
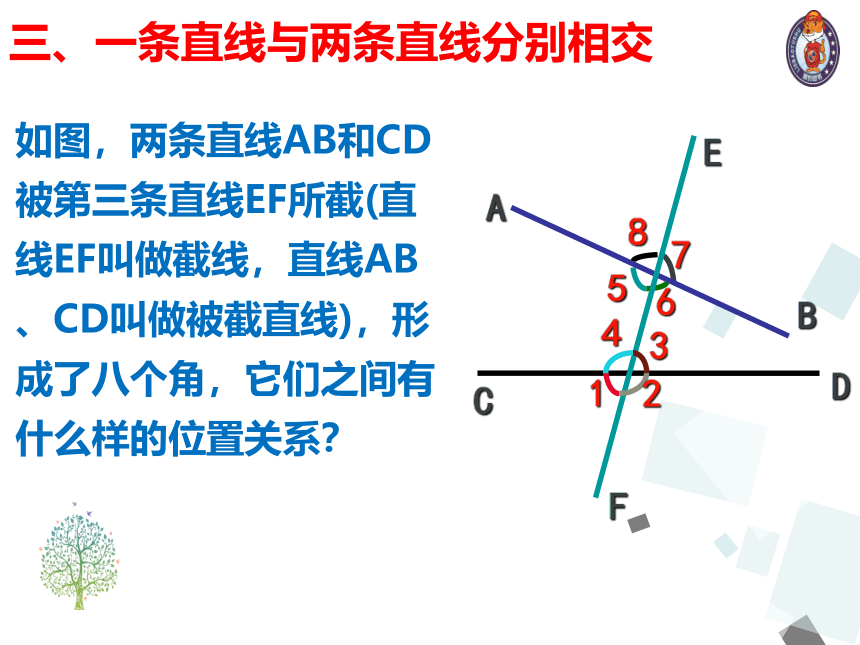
三、一条直线与两条直线分别相交
如图,两条直线AB和CD被第三条直线EF所截(直线EF叫做截线,直线AB、CD叫做被截直线),形成了八个角,它们之间有什么样的位置关系?
5
1
7
8
5
4
1
3
2
6
2
6
7
3
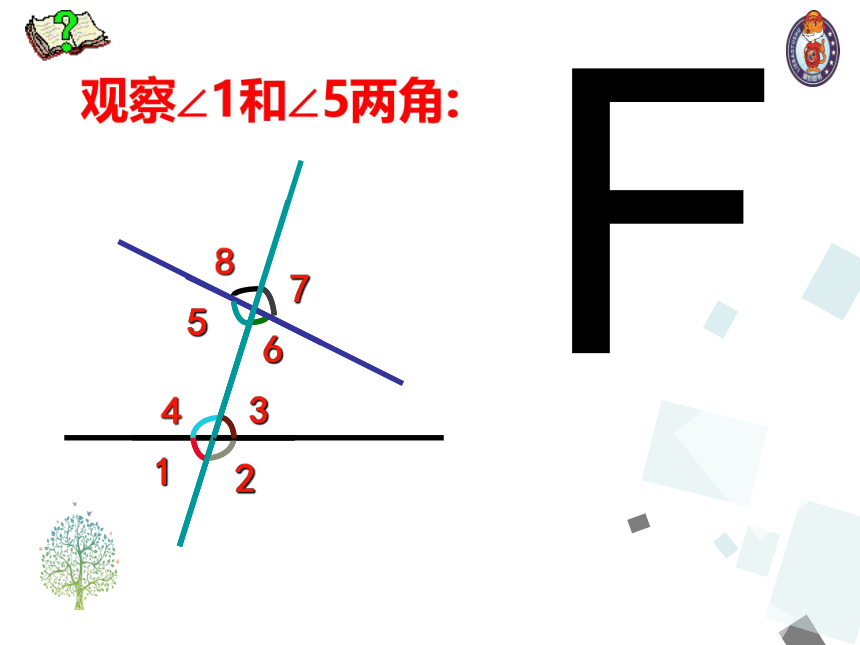
观察∠1和∠5两角:
F
5
1
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有……
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠3和∠5两角:
Z
5
3
内错角
5
3
观察∠3和∠5两角:
夹在两条被截直线内,分别在截线两侧(交错)
7
8
5
4
1
3
2
6
5
3
4
6
图中的内错角除∠3和∠5外,还有……
5
1
7
8
5
4
1
3
2
6
观察∠3和∠6:
3
6
U
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两条被截直线内
7
8
5
4
1
3
2
6
5
4
3
6
图中的同旁内角除∠3和∠6外,还有……
形如字母“U”
(或反置、斜放)
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置、斜放)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或反置、斜放)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
1、下列图中的∠1与∠2是邻补角吗?为什么?
1
2
2
1
(1)
(2)
不是
是
邻补角的特点:
1、顶点相同,
2、有一条公共边,
3、另一边互为反向延长线。
练一练
2、下列各图中∠1、∠2是对顶角吗?为什么?
不是
是
不是
不是
(1)
(2)
(3)
(4)
对顶角的特点:
1、顶点相同,
2、角的两边互为反向延长线。
3、如图,若∠AOD= 90°,
直线AB、CD的位置关系是
E
F
4、若直线AB⊥CD ,则∠AOD=
90 °
AB⊥CD
∵∠AOD=90°(已知),
∴AB⊥CD(垂直的定义).
这个推理过程可以写成:
∵AB⊥CD(已知),
∵∠AOD=90° (垂直的定义) .
这个推理过程可以写成:
A
O
C
B
D
5、如图, ∠1与∠2是_____和_____被_____所截形成的______角。
∠3与∠4是_____和_____被_____所截形成的______角。
AD
BC
AC
内错
AB
CD
AC
内错
6、如图, ∠1与∠2是_____和_____被_____所截形成的 ______ 角。
∠3与∠4是_____和_____被_____所截形成的______角。
AD
BC
CD
同旁内
AB
CD
BE
同位
学习目标:
1.对本小节所学知识进行回顾与思考,把本节内容条理化,系统化.
2.通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言的运用.
如图,任意两条相交直线,在形成的四个角中,两两相配所组成的各对角存在怎样的位置关系
两直线相交 所形成的角 分 类
O
A
B
C
D
)
(
1
3
4
2
)
(
∠3
∠1
∠2
∠4
∠1和∠2
4
∠2和∠
∠ 和∠
∠ 和∠
1
4
3
4
3
∠1和∠3
∠ 和∠
2
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
图中互为邻补角的有:
∠1与∠2, ∠2与∠3,
∠3与∠4, ∠1与∠4.
得出概念:
邻补角
O
C
D
A
B
1
3
4
2
如果一个角的两边是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中互为对顶角的为:
∠1与∠3; ∠2与∠4.
对顶角
O
C
D
A
B
1
3
4
2
得出概念:
1.垂直的定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
如图,a、b互相垂直,点O叫垂足。a叫b的垂线,b也叫a的垂线。
b
a
O
二、两条直线互相垂直
用“⊥”和直线字母表示垂直
2.垂直的表示方法:
如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a
有时为了强调垂足,则记为:a⊥b, 垂足为O.
b
a
O
7
8
5
6
A
B
4
1
3
2
C
D
E
F
三、一条直线与两条直线分别相交
如图,两条直线AB和CD被第三条直线EF所截(直线EF叫做截线,直线AB、CD叫做被截直线),形成了八个角,它们之间有什么样的位置关系?
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠1和∠5两角:
F
5
1
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有……
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠3和∠5两角:
Z
5
3
内错角
5
3
观察∠3和∠5两角:
夹在两条被截直线内,分别在截线两侧(交错)
7
8
5
4
1
3
2
6
5
3
4
6
图中的内错角除∠3和∠5外,还有……
5
1
7
8
5
4
1
3
2
6
观察∠3和∠6:
3
6
U
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两条被截直线内
7
8
5
4
1
3
2
6
5
4
3
6
图中的同旁内角除∠3和∠6外,还有……
形如字母“U”
(或反置、斜放)
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置、斜放)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或反置、斜放)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
1、下列图中的∠1与∠2是邻补角吗?为什么?
1
2
2
1
(1)
(2)
不是
是
邻补角的特点:
1、顶点相同,
2、有一条公共边,
3、另一边互为反向延长线。
练一练
2、下列各图中∠1、∠2是对顶角吗?为什么?
不是
是
不是
不是
(1)
(2)
(3)
(4)
对顶角的特点:
1、顶点相同,
2、角的两边互为反向延长线。
3、如图,若∠AOD= 90°,
直线AB、CD的位置关系是
E
F
4、若直线AB⊥CD ,则∠AOD=
90 °
AB⊥CD
∵∠AOD=90°(已知),
∴AB⊥CD(垂直的定义).
这个推理过程可以写成:
∵AB⊥CD(已知),
∵∠AOD=90° (垂直的定义) .
这个推理过程可以写成:
A
O
C
B
D
5、如图, ∠1与∠2是_____和_____被_____所截形成的______角。
∠3与∠4是_____和_____被_____所截形成的______角。
AD
BC
AC
内错
AB
CD
AC
内错
6、如图, ∠1与∠2是_____和_____被_____所截形成的 ______ 角。
∠3与∠4是_____和_____被_____所截形成的______角。
AD
BC
CD
同旁内
AB
CD
BE
同位
