青岛版小学四年级数学下册《智慧广场—重叠问题》教学建议
文档属性
| 名称 | 青岛版小学四年级数学下册《智慧广场—重叠问题》教学建议 |  | |
| 格式 | doc | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 16:23:08 | ||
图片预览

文档简介
《智慧广场—重叠问题》教学建议
本信息窗呈现的是四年级一班同学假期参加社会实践活动的情况,通过“参加社会实践活动的一共有凡人”的问题,引入对重叠问题的学习。
通过对本信息窗的学习,引导学生学会借助集合图解决重叠问题。
教学时,可以先从学生参加社会实践活动的话题谈起,通过多媒体或者挂图出示情境窗,引导学生观察、交流图中的信息,提出问题“参加社会实践活动一共有几人”,然后利用图中的数学信息展开学习活动。
“合作探索”的问题是:“参加社会实践活动的一共有几人?”教材呈现了学生可能出现的解决问题的方法及教师出示的集合图,展开对重叠问题的学习。
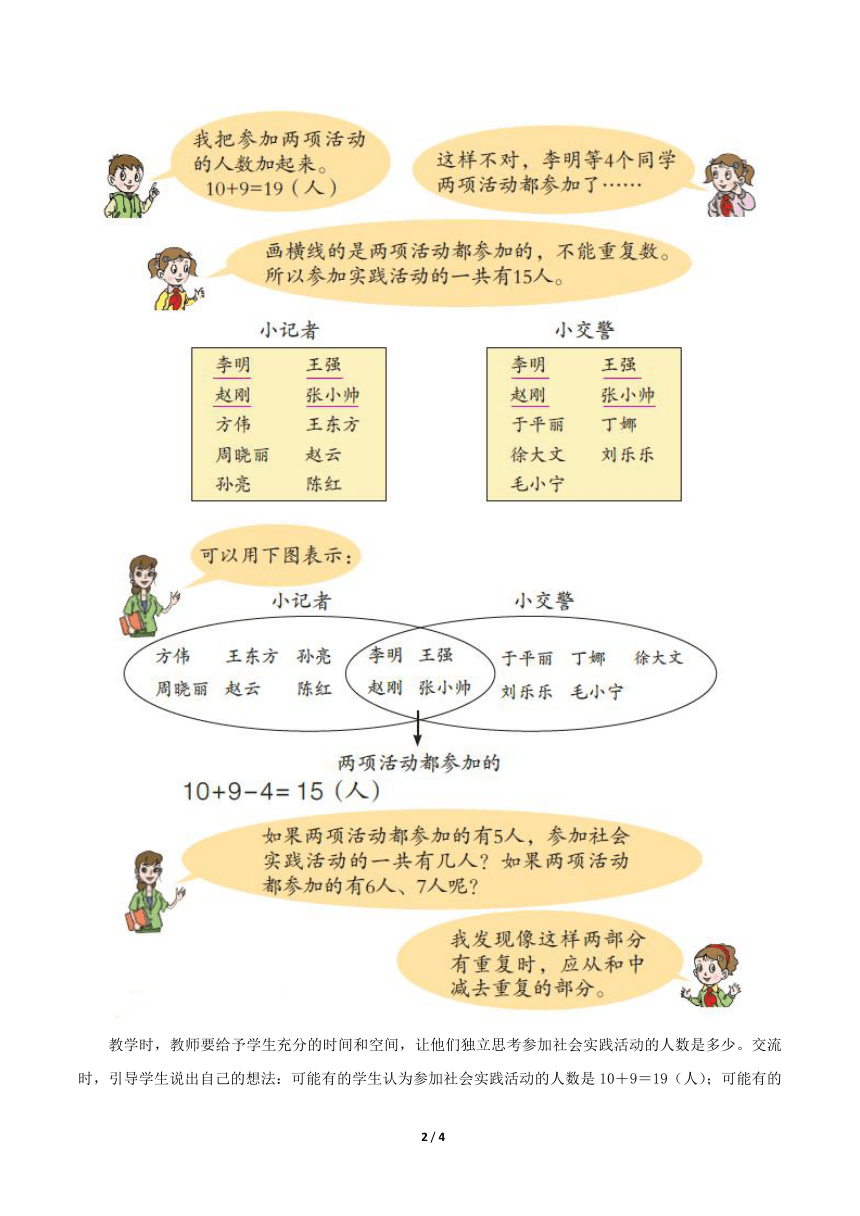
教学时,教师要给予学生充分的时间和空间,让他们独立思考参加社会实践活动的人数是多少。交流时,引导学生说出自己的想法:可能有的学生认为参加社会实践活动的人数是10+9=19(人);可能有的学生已经发现了名单中有重复的,也就是李明、王强、张小帅、赵刚两种实践活动都参加了;还有的学生可能把重复的人数用横线画出来,数出了参加社会实践活动的人数是15人。通过交流探讨,引导学生明确:要求参加实践活动一共有多少人,不能用两种活动的人数直接相加,从而引出本节课要研究的问题——重叠问题。
接着,教师可以组织同桌进行抢姓名卡片比赛(提前把参加社会实践活动的人名做成姓名卡片)。因为同桌两个人都想要“李明、王强、张小帅、赵刚”4张姓名卡片,就引发了矛盾,教师适时引导学生思考:两个人都想要的4张姓名卡片放在什么位置更好?学生可能会想到放在中间。教师继而引导学生进一步思考:能不能用一种直观图来清楚地表示出哪是参加小记者活动的,哪是参加小交警活动的?探讨交流中,学生可能会想到把参加小记者活动的10人圈在一起,把参加小交警活动的9人圈在一起,交叉部分有4个人,他们就是两种活动都参加的。这样引领学生一步步完成直观图(韦恩图),并根据直观图(韦恩图)列出算式解决重叠问题,10+9—4=15(人)。接着,教师可以进一步启动问题:如果两种活动都参加的有5人,参加实践活动的一共有几人?引导学生列出算式:1O+9—5=14(人)。然后启动问题:如果两种活动都参加的有6人、7人呢?最后,通过观察这些算式,共同概括总结出解决重叠问题的方法:先求出两部分人数的总和,再减去重复的也就是两种活动都参加的人数。在以上过程中,学生经历了解决重叠问题的建模过程,积累了基本的数学活动经验。
“自主练习”第1题是求“全班有多少人”的题目,引导学生直接用解决重叠问题的方法独立完成。
第2题是结合生活实际的练习。教师要引导学生在理解“两根竹竿各长230厘米,接头处长50厘米”的基础上,独立完成。
第3、4题是重叠问题的变式题。练习时,先引导学生理解题意,再列式计算,组织交流。
第5题求的是“两种棋都会的有多少人”,这是重叠问题的变形练习。在学生独立思考的基础上,教师要适时引导。解决问题有两种思路:21+17+10-45=2(人);21+17-(45-10)=2(人)。
2 / 4
本信息窗呈现的是四年级一班同学假期参加社会实践活动的情况,通过“参加社会实践活动的一共有凡人”的问题,引入对重叠问题的学习。
通过对本信息窗的学习,引导学生学会借助集合图解决重叠问题。
教学时,可以先从学生参加社会实践活动的话题谈起,通过多媒体或者挂图出示情境窗,引导学生观察、交流图中的信息,提出问题“参加社会实践活动一共有几人”,然后利用图中的数学信息展开学习活动。
“合作探索”的问题是:“参加社会实践活动的一共有几人?”教材呈现了学生可能出现的解决问题的方法及教师出示的集合图,展开对重叠问题的学习。
教学时,教师要给予学生充分的时间和空间,让他们独立思考参加社会实践活动的人数是多少。交流时,引导学生说出自己的想法:可能有的学生认为参加社会实践活动的人数是10+9=19(人);可能有的学生已经发现了名单中有重复的,也就是李明、王强、张小帅、赵刚两种实践活动都参加了;还有的学生可能把重复的人数用横线画出来,数出了参加社会实践活动的人数是15人。通过交流探讨,引导学生明确:要求参加实践活动一共有多少人,不能用两种活动的人数直接相加,从而引出本节课要研究的问题——重叠问题。
接着,教师可以组织同桌进行抢姓名卡片比赛(提前把参加社会实践活动的人名做成姓名卡片)。因为同桌两个人都想要“李明、王强、张小帅、赵刚”4张姓名卡片,就引发了矛盾,教师适时引导学生思考:两个人都想要的4张姓名卡片放在什么位置更好?学生可能会想到放在中间。教师继而引导学生进一步思考:能不能用一种直观图来清楚地表示出哪是参加小记者活动的,哪是参加小交警活动的?探讨交流中,学生可能会想到把参加小记者活动的10人圈在一起,把参加小交警活动的9人圈在一起,交叉部分有4个人,他们就是两种活动都参加的。这样引领学生一步步完成直观图(韦恩图),并根据直观图(韦恩图)列出算式解决重叠问题,10+9—4=15(人)。接着,教师可以进一步启动问题:如果两种活动都参加的有5人,参加实践活动的一共有几人?引导学生列出算式:1O+9—5=14(人)。然后启动问题:如果两种活动都参加的有6人、7人呢?最后,通过观察这些算式,共同概括总结出解决重叠问题的方法:先求出两部分人数的总和,再减去重复的也就是两种活动都参加的人数。在以上过程中,学生经历了解决重叠问题的建模过程,积累了基本的数学活动经验。
“自主练习”第1题是求“全班有多少人”的题目,引导学生直接用解决重叠问题的方法独立完成。
第2题是结合生活实际的练习。教师要引导学生在理解“两根竹竿各长230厘米,接头处长50厘米”的基础上,独立完成。
第3、4题是重叠问题的变式题。练习时,先引导学生理解题意,再列式计算,组织交流。
第5题求的是“两种棋都会的有多少人”,这是重叠问题的变形练习。在学生独立思考的基础上,教师要适时引导。解决问题有两种思路:21+17+10-45=2(人);21+17-(45-10)=2(人)。
2 / 4
