2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.5正态分布课件(共35张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.5正态分布课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 19:26:11 | ||
图片预览





文档简介
(共35张PPT)
现实中,除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量(continuous randomvariable).下面我们看一个具体问题.
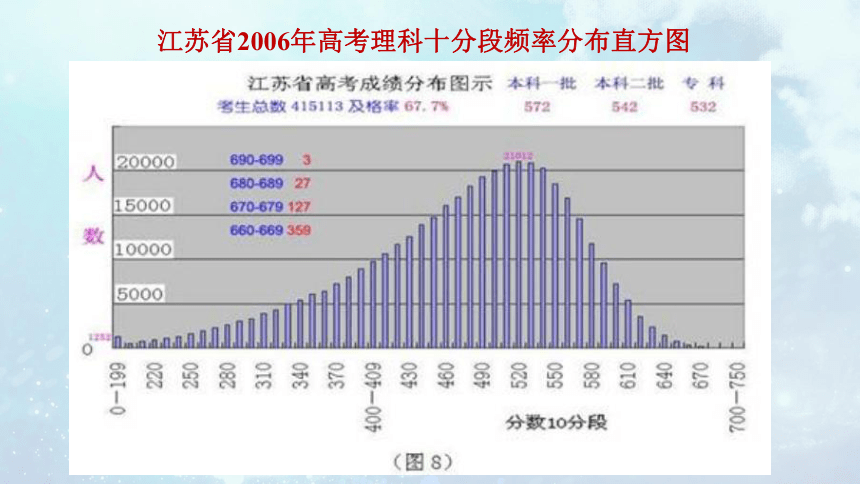
江苏省2006年高考理科十分段频率分布直方图
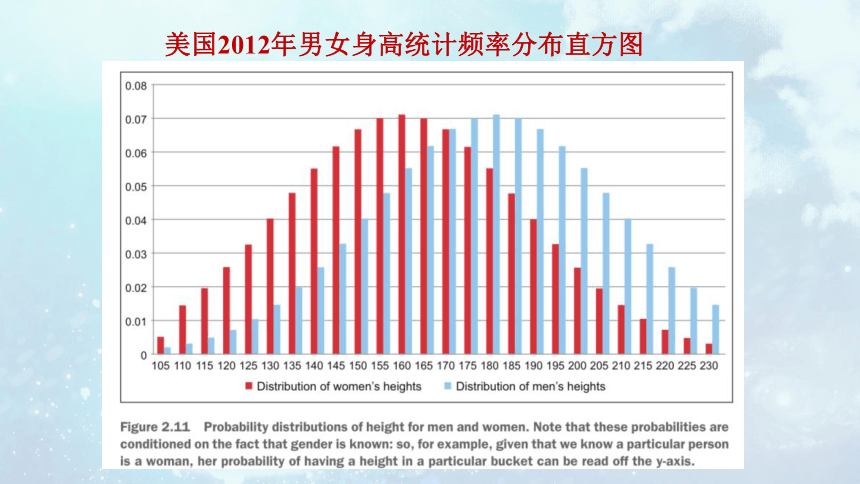
美国2012年男女身高统计频率分布直方图
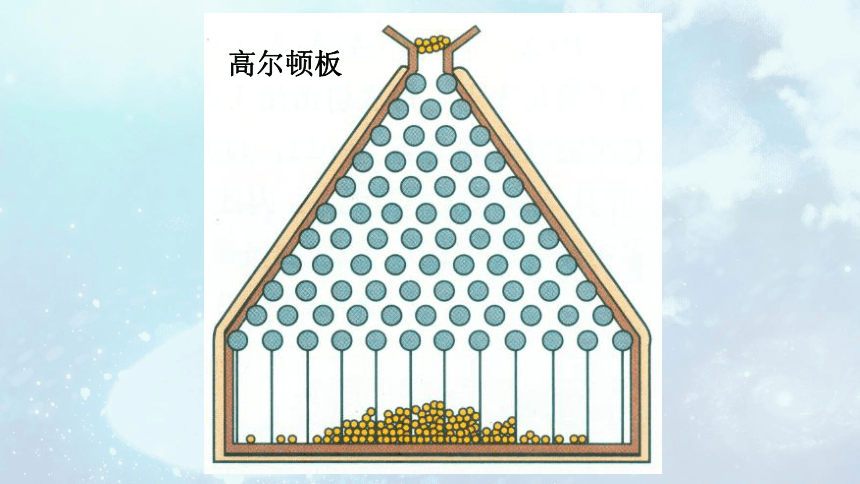
高尔顿板
1
3
5
7
9
球槽编号
频率
组距
11
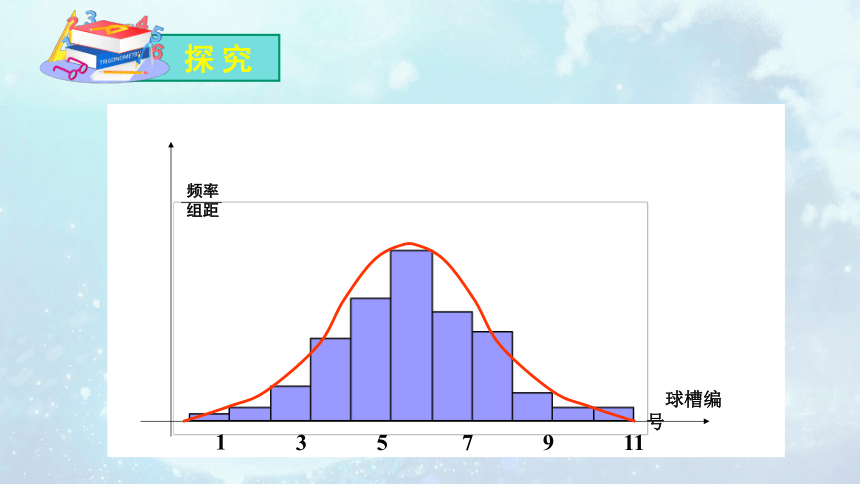
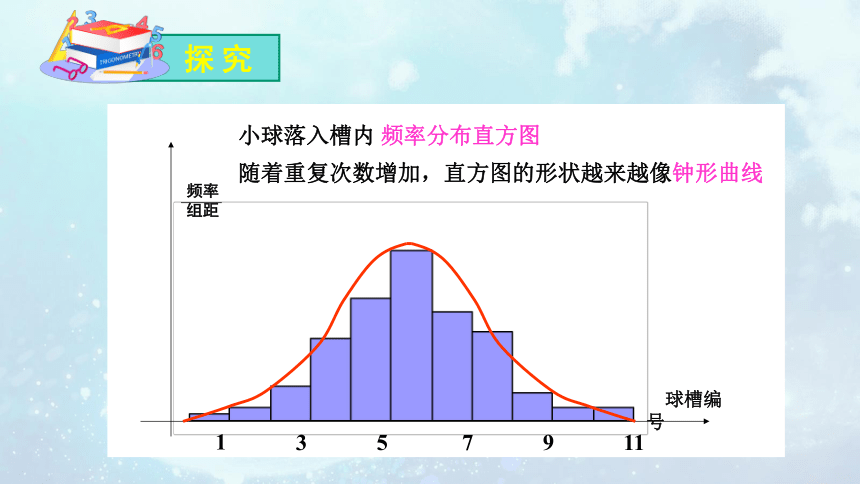
探 究
小球落入槽内 频率分布直方图
1
3
5
7
9
球槽编号
频率
组距
11
随着重复次数增加,直方图的形状越来越像钟形曲线
探 究
在数学家的不懈努力下,找到了以下刻画随机误差分布的解析式:
其中 为参数.
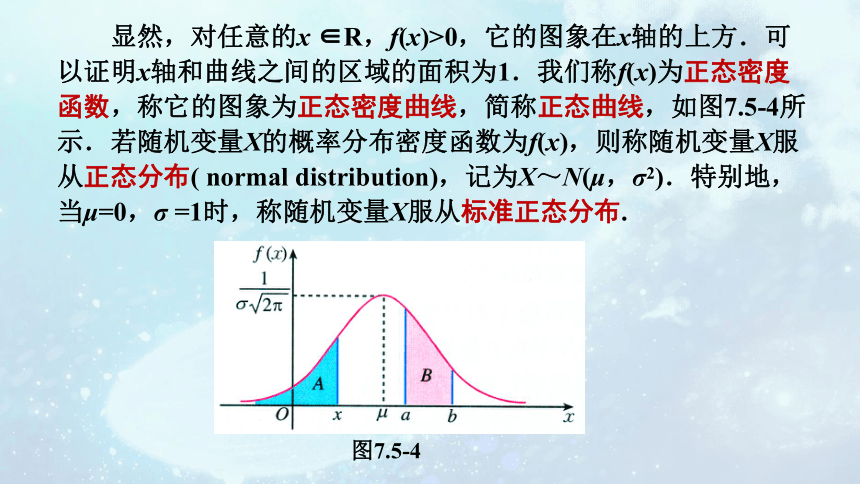
显然,对任意的x ∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如图7.5-4所示.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布( normal distribution),记为X~N(μ,σ2).特别地,当μ=0,σ =1时,称随机变量X服从标准正态分布.
图7.5-4
1
3
5
7
9
球槽编号
频率
组距
11
在生产中,在正常生产条件下各种产品的质量指标;
在测量中,测量结果;
在生物学中,同一群体的某一特征;……;
在气象中,某地每年七月份的平均气温、平均湿度以及降
雨量等,水文中的水位;
正态分布广泛存在于自然界、生产及科学技术的许多领域中。正态分布在概率和统计中占有重要地位。
在实际遇到的许多随机现象都服从或近似服从正态分布:
0
x
y
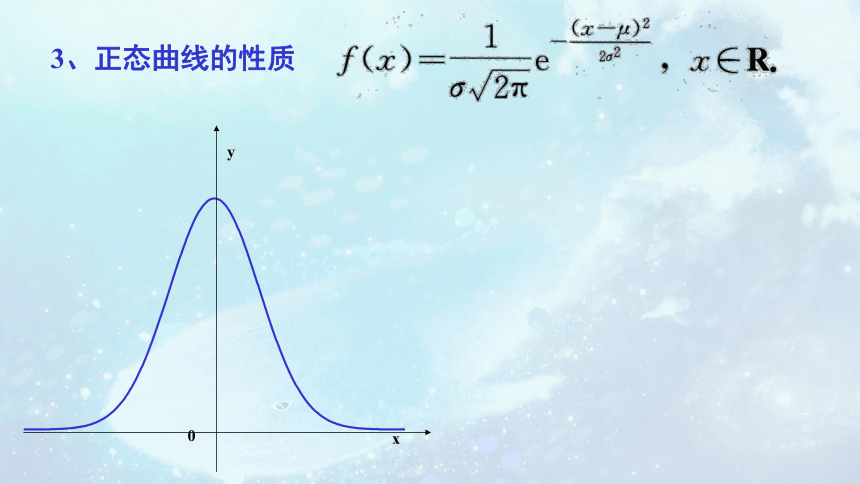
3、正态曲线的性质
0
x
y
3、正态曲线的性质
(3)当|x|无限增大时,曲线无限接近x轴
(1)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1
(2)曲线在x=μ处达到峰值(最高点)
3
1
2
σ=0.5
μ=-1
μ=0
μ=1
m 的意义:
3
1
2
σ=0.5
μ=-1
μ=0
μ=1
m 的意义:
反映总体随机变量取值的集中位置,即为均值.
=0.5
=1
=2
μ=0
s的意义:
=0.5
=1
=2
μ=0
s的意义:
反映随机变量的分布相对于均值μ的离散程度,即为标准差
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
4、正态曲线的结论
若X~N(μ,s2),则E(X)=μ,D(X)=s2
例 李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,样本方差为36;骑自行车平均用时34 min,样本方差为4.假设坐公交车用时X和骑自行车用时Y
都服从正态分布.
(1)估计X,Y的分布中的参数;
(2) 根据(1)中的估计结果,利
用信息技术工具画出X和Y的
分布密度曲线;
(3) 如果某天有38 min可用,李
明应选择哪种交通工具 如果
某天只有34 min可用,又应该
选择哪种交通工具 请说明理由.
图7.5-8
由此看到,尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X 的取值几乎总是落在区间[μ-3σ,μ+3σ]内,而在此区间以外取值的概率大约只有0.0027,通常认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布N (μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ 原则.
S(-x2 ,-x1)
-x2 - x1 x1 x2
S(x1,x2)=S(-x2,-x1)
正态曲线下的面积规律
对称区域面积相等。
例1、已知 ,且 ,
则 等于 ( )
A. 0.1 B. 0.2
C. 0.3 D. 0.4
A
例1、已知 ,且 ,
则 等于 ( )
A. 0.1 B. 0.2
C. 0.3 D. 0.4
2、设离散型随机变量X~N(0,1), 则 = ,
= .
3、 已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
4、若X~N(5,1), 求P(62、设离散型随机变量X~N(0,1), 则 = ,
= .
3、 已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
4、若X~N(5,1), 求P(6D
0.5
0.9545
0.1359
5、已知一次考试共有60名同学参加,考生的成绩X~ ,据此估计,大约应有57人的分数在下列哪个区间内? ( )
A. (90,110] B. (95,125]
C. (100,120] D. (105,115]
5、已知一次考试共有60名同学参加,考生的成绩X~ ,据此估计,大约应有57人的分数在下列哪个区间内? ( )
A. (90,110] B. (95,125]
C. (100,120] D. (105,115]
A
1.正态分布密度曲线函数;
2.正态曲线的性质;
3. 原则
知识小结
练习:
1、若一个正态分布的概率函数是一个偶函数且该函数的最大值等于 ,求该正态分布的概率密度函数的解析式。
20
25
30
15
10
x
y
5
35
2、如图,是一个正态曲线,试根据图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差。
《考一本》第25课时
根据频率与概率的关系,可用图7.5-3中的钟形曲线(曲线与水平轴之间的区域的面积为1)来描述袋装食盐质量误差的概率分布.例如,任意抽取一袋食盐,误差落在[-2,-1]内的概率,可用图中黄色阴影部分的
面积表示.
由函数知识可知,图7.5-3
中的钟形曲线是一个函数.那
么,这个函数是否存在解析式
呢
图7.5-3
思 考
一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响?它们反映正态分布的哪些特征
我们知道,函数y=f(x-p)的图
象可由y= f(x)的图象平移得到.因
此,在参数σ取固定值时,正态曲
线的位置由μ确定,且随着μ的变
化而沿x轴平移,如图7.5-5所示.
图7.5-5
当μ取定值时,因为正态曲线的峰值 与σ成反比,而且
对任意的σ>0,正态曲线与x轴之间的区域的面积总为1. 因此,当σ较小时,峰值高,正态曲线“瘦高”,表示随机变量X的分布比较集中;当σ较大时,峰值低,正态曲线“矮胖”,表示随机变量X的分布比较分散,如图7.5-6所示.
图7.5-6
观察图7.5-5和图7.5-6可以发现,参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于均值μ的离散程度.实际上,我们有
若X~N(μ,σ2),则E(X)=μ,D(X)=σ2.
图7.5-5
图7.5-6
现实中,除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量(continuous randomvariable).下面我们看一个具体问题.
江苏省2006年高考理科十分段频率分布直方图
美国2012年男女身高统计频率分布直方图
高尔顿板
1
3
5
7
9
球槽编号
频率
组距
11
探 究
小球落入槽内 频率分布直方图
1
3
5
7
9
球槽编号
频率
组距
11
随着重复次数增加,直方图的形状越来越像钟形曲线
探 究
在数学家的不懈努力下,找到了以下刻画随机误差分布的解析式:
其中 为参数.
显然,对任意的x ∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如图7.5-4所示.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布( normal distribution),记为X~N(μ,σ2).特别地,当μ=0,σ =1时,称随机变量X服从标准正态分布.
图7.5-4
1
3
5
7
9
球槽编号
频率
组距
11
在生产中,在正常生产条件下各种产品的质量指标;
在测量中,测量结果;
在生物学中,同一群体的某一特征;……;
在气象中,某地每年七月份的平均气温、平均湿度以及降
雨量等,水文中的水位;
正态分布广泛存在于自然界、生产及科学技术的许多领域中。正态分布在概率和统计中占有重要地位。
在实际遇到的许多随机现象都服从或近似服从正态分布:
0
x
y
3、正态曲线的性质
0
x
y
3、正态曲线的性质
(3)当|x|无限增大时,曲线无限接近x轴
(1)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1
(2)曲线在x=μ处达到峰值(最高点)
3
1
2
σ=0.5
μ=-1
μ=0
μ=1
m 的意义:
3
1
2
σ=0.5
μ=-1
μ=0
μ=1
m 的意义:
反映总体随机变量取值的集中位置,即为均值.
=0.5
=1
=2
μ=0
s的意义:
=0.5
=1
=2
μ=0
s的意义:
反映随机变量的分布相对于均值μ的离散程度,即为标准差
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
4、正态曲线的结论
若X~N(μ,s2),则E(X)=μ,D(X)=s2
例 李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,样本方差为36;骑自行车平均用时34 min,样本方差为4.假设坐公交车用时X和骑自行车用时Y
都服从正态分布.
(1)估计X,Y的分布中的参数;
(2) 根据(1)中的估计结果,利
用信息技术工具画出X和Y的
分布密度曲线;
(3) 如果某天有38 min可用,李
明应选择哪种交通工具 如果
某天只有34 min可用,又应该
选择哪种交通工具 请说明理由.
图7.5-8
由此看到,尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X 的取值几乎总是落在区间[μ-3σ,μ+3σ]内,而在此区间以外取值的概率大约只有0.0027,通常认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布N (μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ 原则.
S(-x2 ,-x1)
-x2 - x1 x1 x2
S(x1,x2)=S(-x2,-x1)
正态曲线下的面积规律
对称区域面积相等。
例1、已知 ,且 ,
则 等于 ( )
A. 0.1 B. 0.2
C. 0.3 D. 0.4
A
例1、已知 ,且 ,
则 等于 ( )
A. 0.1 B. 0.2
C. 0.3 D. 0.4
2、设离散型随机变量X~N(0,1), 则 = ,
= .
3、 已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
4、若X~N(5,1), 求P(6
= .
3、 已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
4、若X~N(5,1), 求P(6
0.5
0.9545
0.1359
5、已知一次考试共有60名同学参加,考生的成绩X~ ,据此估计,大约应有57人的分数在下列哪个区间内? ( )
A. (90,110] B. (95,125]
C. (100,120] D. (105,115]
5、已知一次考试共有60名同学参加,考生的成绩X~ ,据此估计,大约应有57人的分数在下列哪个区间内? ( )
A. (90,110] B. (95,125]
C. (100,120] D. (105,115]
A
1.正态分布密度曲线函数;
2.正态曲线的性质;
3. 原则
知识小结
练习:
1、若一个正态分布的概率函数是一个偶函数且该函数的最大值等于 ,求该正态分布的概率密度函数的解析式。
20
25
30
15
10
x
y
5
35
2、如图,是一个正态曲线,试根据图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差。
《考一本》第25课时
根据频率与概率的关系,可用图7.5-3中的钟形曲线(曲线与水平轴之间的区域的面积为1)来描述袋装食盐质量误差的概率分布.例如,任意抽取一袋食盐,误差落在[-2,-1]内的概率,可用图中黄色阴影部分的
面积表示.
由函数知识可知,图7.5-3
中的钟形曲线是一个函数.那
么,这个函数是否存在解析式
呢
图7.5-3
思 考
一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响?它们反映正态分布的哪些特征
我们知道,函数y=f(x-p)的图
象可由y= f(x)的图象平移得到.因
此,在参数σ取固定值时,正态曲
线的位置由μ确定,且随着μ的变
化而沿x轴平移,如图7.5-5所示.
图7.5-5
当μ取定值时,因为正态曲线的峰值 与σ成反比,而且
对任意的σ>0,正态曲线与x轴之间的区域的面积总为1. 因此,当σ较小时,峰值高,正态曲线“瘦高”,表示随机变量X的分布比较集中;当σ较大时,峰值低,正态曲线“矮胖”,表示随机变量X的分布比较分散,如图7.5-6所示.
图7.5-6
观察图7.5-5和图7.5-6可以发现,参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于均值μ的离散程度.实际上,我们有
若X~N(μ,σ2),则E(X)=μ,D(X)=σ2.
图7.5-5
图7.5-6
