青岛版小学四年级数学下册《平均数(信息窗1)》教学设计
文档属性
| 名称 | 青岛版小学四年级数学下册《平均数(信息窗1)》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 615.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 21:56:29 | ||
图片预览


文档简介
《平均数(信息窗1)》教学设计
教学内容:教科书第91~92页,平均数的意义。
教学目标:
1.结合生活实例,理解平均数的意义,探索求平均数的基本方法,初步学会根据具体情况运用平均数分析与解决实际问题,根据统计结果作出简单的判断和预测。
2.在具体情境中培养整理数据、分析数据的意识和能力,体会统计的作用及其价值。
3.使学生进一步体会数学与生活的密切联系,体验运用数学知识解决问题的乐趣,培养学生善于观察、勤于思考、勇于探索的良好学习习惯。
教学重点:理解平均数的意义、求平均数的方法。
教学难点:理解平均数的意义。
教学过程:
1.创设情境,引出并初步认识平均数。
师:同学们喜欢体育运动吗?能告诉大家你喜欢哪些体育运动吗?
生1:跳远。
生2:踢足球。
生3:打篮球。
…………
师:老师和你一样,也喜欢打篮球。请看——(多媒体出示课本情境图及7、8号运动员在小组赛中得分情况统计表)从成绩记录中你有什么不明白的地方吗?
生:横线表示什么?
师:横线表示没上场。
师:仔细分析7号和8号的得分情况,思考一下谁的投篮水平高。
生l:我算了一下,7号在小组赛中共得了9+11+13=33(分),8号共得了7+13+12+8=40(分)。所以我们认为8号投篮水平高。
生2:我也算了两名队员在小组赛中的总得分,8号队员得分多,所以我也认为8号投篮水平高。
师:(用目光巡视其他同学)你们同意吗?
生3:不同意,7号上场3次,8号上场4次,上场次数不一样,比总分不公平!
师:比总分不公平,怎样比才公平?
生4:7号最少得9分,8号最少才得7分,所以7号的投篮水平高。
生5:这样也不行,你可以比较最少的,我也可以比较最多的,7号最多得13分,8号最多也得13分,难道他们的投篮水平一样高?
师:说得有道理17号和8号每人每场的得分不一样,比其中一场的得分就不好比了,那怎么办?
生6:如果能把7号和8号运动员每场得的分数变得一样多,就可以比了。
师:这位同学的意思是把7号运动员的每场得分匀一匀,变得同样多,把8号运动员的每场得分匀一匀,变得同样多,然后再来比,这样可以吗?
(学生都表示同意。)
师:像这样,把几个数“匀一匀”,使每个数变得同样多,在数学上有一个专门的名字,叫作“平均数”。今天这节课,我们就来一起认识它。(板书课题。)
【评析:在生活中,人们常用平均数来表示一组数据的整体水平,用它来反映统计对象的一般情况。然而,对于孩子而言,平均数又是抽象的、难以理解的。执教者依托教材,巧妙创设“篮球比赛中队员受伤,7号和8号两名篮球运动员到底该换谁上场”这个富有挑战性的问题,引导学生在熟知的生活情境中应.用已有的知识经验解决问题,既激发了学生的探究欲望,同时也在解决问题的过程中自然地引出了平均数,化抽象为形象,学生主动体会了平均数的意义和作用。】
2.探究求平均数的策略与方法。
(1)“移多补少”理解平均数的含义和统计的意义。
师:那么,我们就先来求一求7号队员的平均得分是多少。
(课件出示7号运动员得分统计表。)
师:请小组长拿出学具袋,同学们可以借助统计图,也可以算一算得出7号运动员的平均每场得分,我们比一比哪个小组的办法好。(小组活动。)
师:哪个小组愿意上来展示一下你们的方法?
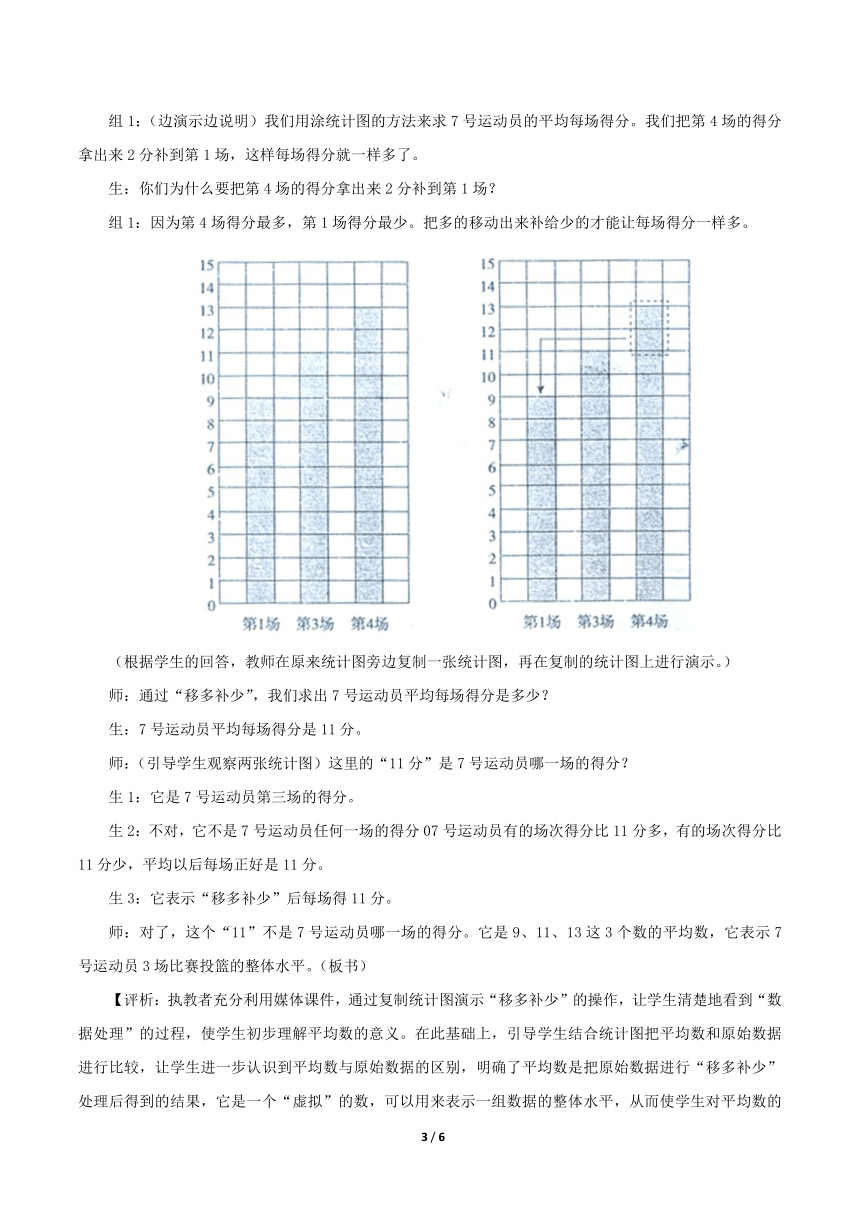
组1:(边演示边说明)我们用涂统计图的方法来求7号运动员的平均每场得分。我们把第4场的得分拿出来2分补到第1场,这样每场得分就一样多了。
生:你们为什么要把第4场的得分拿出来2分补到第1场?
组1:因为第4场得分最多,第1场得分最少。把多的移动出来补给少的才能让每场得分一样多。
(根据学生的回答,教师在原来统计图旁边复制一张统计图,再在复制的统计图上进行演示。)
师:通过“移多补少”,我们求出7号运动员平均每场得分是多少?
生:7号运动员平均每场得分是11分。
师:(引导学生观察两张统计图)这里的“11分”是7号运动员哪一场的得分?
生1:它是7号运动员第三场的得分。
生2:不对,它不是7号运动员任何一场的得分07号运动员有的场次得分比11分多,有的场次得分比11分少,平均以后每场正好是11分。
生3:它表示“移多补少”后每场得11分。
师:对了,这个“11”不是7号运动员哪一场的得分。它是9、11、13这3个数的平均数,它表示7号运动员3场比赛投篮的整体水平。(板书)
【评析:执教者充分利用媒体课件,通过复制统计图演示“移多补少”的操作,让学生清楚地看到“数据处理”的过程,使学生初步理解平均数的意义。在此基础上,引导学生结合统计图把平均数和原始数据进行比较,让学生进一步认识到平均数与原始数据的区别,明确了平均数是把原始数据进行“移多补少”处理后得到的结果,它是一个“虚拟”的数,可以用来表示一组数据的整体水平,从而使学生对平均数的统计意义有了更清晰的认识。】
(2)探索算法,掌握求平均数的一般方法。
师:还有选用其他方法的吗?我刚才看到有不少同学用纸笔在计算。
组2:我们是这样算的:9+11+13=33(分),再用33÷3=11(分)。(教师板书。)
师:能说说你们是怎么想的吗?
生:我们先求7号一共得了多少分,再除以4场求平均每场得多少分。
师:这是一种“先求总数,再求平均数”的方法,和我们刚才“移多补少”的方法得出的结果相同吗?
生:相同。
师:8号运动员的平均得分是多少呢?请你选一种自己喜欢的方法求一求。
师:谁来介绍一下你的方法?.
(一名学生口述“移多补少”的过程,教师根据学生的口述,课件演示。另一名学生用“先求总数,再求平均数”的方法。)
师:这里的“10分”是8号运动员哪一场的得分?
生:它不是8号运动员哪一场的得分,它是7、13、12、8这4个数的平均数,它表示的是8号运动员4场比赛投篮的整体水平。(板书。)
师:同学们,现在你能确定派谁上场了吗?说说你的理由。
生:派7号上场,因为7号的平均数高。
师:7号的平均分高决定了7号运动员投篮的整体水平要高一些。
【评析:教师积极地为学生创设自主探究、合作交流的空间,让学生在动手、动口、动脑多种感官协同运作的过程中经历了“平均数”的形成过程,感悟到“求平均数”的多种方法。】
3.走进生活,应用新知。
(1)变式练习,巩固新知。
师:为了取得好成绩,篮球队员平日的身体素质训练是非常辛苦的,我们一起来看看他们分组训练时1分钟拍球成绩统计图。(课件出示。)
师:他们三个人的平均成绩是多少呢?请你先来估计一下。
生1:37个。
生2:38个。
…………
师:你们这样估计有根据吗?
生3:平均数肯定比最大的那个数小,比最小的那个数大。
师:你的这个发现太棒了。同学们估计得准不准呢?请你用自己的方法算算看。
(学生独立完成。)
师:谁来说说你的方法?
生:我用“移多补少”的方法,从41里拿3个给35,三个人就一样多了,都是38个。
师:平均拍38个和李丽拍的38个表示的意义相同吗?
生:不同。
(出示6个同学分别拍了35、41、38、31、43、40个。)
师:现在平均每人拍多少个?
生:(35+41+38+31+43+40)÷6=38(个)。
师:为什么不用“移多补少”的方法?
(学生讨论交流后明确:当数据比较复杂时,通常运用“先求总数,再求平均数”的方法计算。)
【评析:巩固练习来源于教材,教师在备课时做了深入的挖掘和处理,通过“拍球”的一组练习,既可以帮助学生进一步理解平均数的意义和计算方法,同时教师适当地引导学生进行“估计”,有效地提升了学生对平均数的认识。】
(2)深化拓展,应用新知。
师:乐于助人的小刚遇到难题了,咱们一起去看看。
一群男孩子正在踢足球,不小心把足球踢到旁边的小河里了,个子最高的小刚自告奋勇地要下水捞足球。(课件出示。)
(此题一出,全班同学迅速地分成两大阵营,一组认为没有危险,一组认为有危险。)
甲方:我们认为小刚不会有危险,因为小刚身高140厘米,而平均水深只有110厘米,小刚站在小河里水不会没过他的头。
乙方:请问甲方,什么叫平均水深?
甲方:平均水深嘛,就是深水和浅水匀乎匀乎,中间的那个数。
乙方(紧追不舍):也就是说不是水下每个地方都是l10厘米深,有的地方比110厘米深,有的地方比110厘米浅。那么,如果小刚站在了深水的地方呢?
(甲方同学吱吱呜呜说不出话来了,很不好意思地站到了乙方的阵营里。)
【评析:将平均数的问题深化到现实生活的层面,在应用“平均水深”解决问题的过程中,让学生进一步体验了事件发生的随机性,提高了学生的实际应用能力。】
(课件出示:据《2011年中国统计年鉴》显示:我国森林总面积约为19545.22万公顷,位居世界第5位;人均森林总面积约为0.15公顷,仅相当于世界人均拥有量的,在世界排120位。)
师:看了这条信息,你有什么想法?你还能找到这样的平均数吗?
【评析:数学来源于生活,必然服务于生活。提供给学生实实在在的社会生活资料,让学生深入理解平均数的意义,感受平均数在生活中的应用,同时也在此过程中让学生得到了适时的环保教育。】
1 / 6
教学内容:教科书第91~92页,平均数的意义。
教学目标:
1.结合生活实例,理解平均数的意义,探索求平均数的基本方法,初步学会根据具体情况运用平均数分析与解决实际问题,根据统计结果作出简单的判断和预测。
2.在具体情境中培养整理数据、分析数据的意识和能力,体会统计的作用及其价值。
3.使学生进一步体会数学与生活的密切联系,体验运用数学知识解决问题的乐趣,培养学生善于观察、勤于思考、勇于探索的良好学习习惯。
教学重点:理解平均数的意义、求平均数的方法。
教学难点:理解平均数的意义。
教学过程:
1.创设情境,引出并初步认识平均数。
师:同学们喜欢体育运动吗?能告诉大家你喜欢哪些体育运动吗?
生1:跳远。
生2:踢足球。
生3:打篮球。
…………
师:老师和你一样,也喜欢打篮球。请看——(多媒体出示课本情境图及7、8号运动员在小组赛中得分情况统计表)从成绩记录中你有什么不明白的地方吗?
生:横线表示什么?
师:横线表示没上场。
师:仔细分析7号和8号的得分情况,思考一下谁的投篮水平高。
生l:我算了一下,7号在小组赛中共得了9+11+13=33(分),8号共得了7+13+12+8=40(分)。所以我们认为8号投篮水平高。
生2:我也算了两名队员在小组赛中的总得分,8号队员得分多,所以我也认为8号投篮水平高。
师:(用目光巡视其他同学)你们同意吗?
生3:不同意,7号上场3次,8号上场4次,上场次数不一样,比总分不公平!
师:比总分不公平,怎样比才公平?
生4:7号最少得9分,8号最少才得7分,所以7号的投篮水平高。
生5:这样也不行,你可以比较最少的,我也可以比较最多的,7号最多得13分,8号最多也得13分,难道他们的投篮水平一样高?
师:说得有道理17号和8号每人每场的得分不一样,比其中一场的得分就不好比了,那怎么办?
生6:如果能把7号和8号运动员每场得的分数变得一样多,就可以比了。
师:这位同学的意思是把7号运动员的每场得分匀一匀,变得同样多,把8号运动员的每场得分匀一匀,变得同样多,然后再来比,这样可以吗?
(学生都表示同意。)
师:像这样,把几个数“匀一匀”,使每个数变得同样多,在数学上有一个专门的名字,叫作“平均数”。今天这节课,我们就来一起认识它。(板书课题。)
【评析:在生活中,人们常用平均数来表示一组数据的整体水平,用它来反映统计对象的一般情况。然而,对于孩子而言,平均数又是抽象的、难以理解的。执教者依托教材,巧妙创设“篮球比赛中队员受伤,7号和8号两名篮球运动员到底该换谁上场”这个富有挑战性的问题,引导学生在熟知的生活情境中应.用已有的知识经验解决问题,既激发了学生的探究欲望,同时也在解决问题的过程中自然地引出了平均数,化抽象为形象,学生主动体会了平均数的意义和作用。】
2.探究求平均数的策略与方法。
(1)“移多补少”理解平均数的含义和统计的意义。
师:那么,我们就先来求一求7号队员的平均得分是多少。
(课件出示7号运动员得分统计表。)
师:请小组长拿出学具袋,同学们可以借助统计图,也可以算一算得出7号运动员的平均每场得分,我们比一比哪个小组的办法好。(小组活动。)
师:哪个小组愿意上来展示一下你们的方法?
组1:(边演示边说明)我们用涂统计图的方法来求7号运动员的平均每场得分。我们把第4场的得分拿出来2分补到第1场,这样每场得分就一样多了。
生:你们为什么要把第4场的得分拿出来2分补到第1场?
组1:因为第4场得分最多,第1场得分最少。把多的移动出来补给少的才能让每场得分一样多。
(根据学生的回答,教师在原来统计图旁边复制一张统计图,再在复制的统计图上进行演示。)
师:通过“移多补少”,我们求出7号运动员平均每场得分是多少?
生:7号运动员平均每场得分是11分。
师:(引导学生观察两张统计图)这里的“11分”是7号运动员哪一场的得分?
生1:它是7号运动员第三场的得分。
生2:不对,它不是7号运动员任何一场的得分07号运动员有的场次得分比11分多,有的场次得分比11分少,平均以后每场正好是11分。
生3:它表示“移多补少”后每场得11分。
师:对了,这个“11”不是7号运动员哪一场的得分。它是9、11、13这3个数的平均数,它表示7号运动员3场比赛投篮的整体水平。(板书)
【评析:执教者充分利用媒体课件,通过复制统计图演示“移多补少”的操作,让学生清楚地看到“数据处理”的过程,使学生初步理解平均数的意义。在此基础上,引导学生结合统计图把平均数和原始数据进行比较,让学生进一步认识到平均数与原始数据的区别,明确了平均数是把原始数据进行“移多补少”处理后得到的结果,它是一个“虚拟”的数,可以用来表示一组数据的整体水平,从而使学生对平均数的统计意义有了更清晰的认识。】
(2)探索算法,掌握求平均数的一般方法。
师:还有选用其他方法的吗?我刚才看到有不少同学用纸笔在计算。
组2:我们是这样算的:9+11+13=33(分),再用33÷3=11(分)。(教师板书。)
师:能说说你们是怎么想的吗?
生:我们先求7号一共得了多少分,再除以4场求平均每场得多少分。
师:这是一种“先求总数,再求平均数”的方法,和我们刚才“移多补少”的方法得出的结果相同吗?
生:相同。
师:8号运动员的平均得分是多少呢?请你选一种自己喜欢的方法求一求。
师:谁来介绍一下你的方法?.
(一名学生口述“移多补少”的过程,教师根据学生的口述,课件演示。另一名学生用“先求总数,再求平均数”的方法。)
师:这里的“10分”是8号运动员哪一场的得分?
生:它不是8号运动员哪一场的得分,它是7、13、12、8这4个数的平均数,它表示的是8号运动员4场比赛投篮的整体水平。(板书。)
师:同学们,现在你能确定派谁上场了吗?说说你的理由。
生:派7号上场,因为7号的平均数高。
师:7号的平均分高决定了7号运动员投篮的整体水平要高一些。
【评析:教师积极地为学生创设自主探究、合作交流的空间,让学生在动手、动口、动脑多种感官协同运作的过程中经历了“平均数”的形成过程,感悟到“求平均数”的多种方法。】
3.走进生活,应用新知。
(1)变式练习,巩固新知。
师:为了取得好成绩,篮球队员平日的身体素质训练是非常辛苦的,我们一起来看看他们分组训练时1分钟拍球成绩统计图。(课件出示。)
师:他们三个人的平均成绩是多少呢?请你先来估计一下。
生1:37个。
生2:38个。
…………
师:你们这样估计有根据吗?
生3:平均数肯定比最大的那个数小,比最小的那个数大。
师:你的这个发现太棒了。同学们估计得准不准呢?请你用自己的方法算算看。
(学生独立完成。)
师:谁来说说你的方法?
生:我用“移多补少”的方法,从41里拿3个给35,三个人就一样多了,都是38个。
师:平均拍38个和李丽拍的38个表示的意义相同吗?
生:不同。
(出示6个同学分别拍了35、41、38、31、43、40个。)
师:现在平均每人拍多少个?
生:(35+41+38+31+43+40)÷6=38(个)。
师:为什么不用“移多补少”的方法?
(学生讨论交流后明确:当数据比较复杂时,通常运用“先求总数,再求平均数”的方法计算。)
【评析:巩固练习来源于教材,教师在备课时做了深入的挖掘和处理,通过“拍球”的一组练习,既可以帮助学生进一步理解平均数的意义和计算方法,同时教师适当地引导学生进行“估计”,有效地提升了学生对平均数的认识。】
(2)深化拓展,应用新知。
师:乐于助人的小刚遇到难题了,咱们一起去看看。
一群男孩子正在踢足球,不小心把足球踢到旁边的小河里了,个子最高的小刚自告奋勇地要下水捞足球。(课件出示。)
(此题一出,全班同学迅速地分成两大阵营,一组认为没有危险,一组认为有危险。)
甲方:我们认为小刚不会有危险,因为小刚身高140厘米,而平均水深只有110厘米,小刚站在小河里水不会没过他的头。
乙方:请问甲方,什么叫平均水深?
甲方:平均水深嘛,就是深水和浅水匀乎匀乎,中间的那个数。
乙方(紧追不舍):也就是说不是水下每个地方都是l10厘米深,有的地方比110厘米深,有的地方比110厘米浅。那么,如果小刚站在了深水的地方呢?
(甲方同学吱吱呜呜说不出话来了,很不好意思地站到了乙方的阵营里。)
【评析:将平均数的问题深化到现实生活的层面,在应用“平均水深”解决问题的过程中,让学生进一步体验了事件发生的随机性,提高了学生的实际应用能力。】
(课件出示:据《2011年中国统计年鉴》显示:我国森林总面积约为19545.22万公顷,位居世界第5位;人均森林总面积约为0.15公顷,仅相当于世界人均拥有量的,在世界排120位。)
师:看了这条信息,你有什么想法?你还能找到这样的平均数吗?
【评析:数学来源于生活,必然服务于生活。提供给学生实实在在的社会生活资料,让学生深入理解平均数的意义,感受平均数在生活中的应用,同时也在此过程中让学生得到了适时的环保教育。】
1 / 6
