人教版九年级下册数学同步课时作业28.2.2 第1课时 仰角、俯角(含答案)
文档属性
| 名称 | 人教版九年级下册数学同步课时作业28.2.2 第1课时 仰角、俯角(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 19:48:18 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第1课时 仰角、俯角
1. 如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β.已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asin α+asin β B.acos α+acos β
C.atan α+atan β D.+
2. 如图,为安全起见,游乐园拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 m B.2 m C.3 m D.3 m
3. 如图所示的钓鱼竿AC长6 m,露在水面上的鱼线BC长3 m,钓者想看看鱼钩上的情况,把鱼竿AC逆时针转动15°到AC'的位置,此时露在水面上的鱼线B'C'的长度是( )
A.4 m B.3 m C.2 m D.3 m
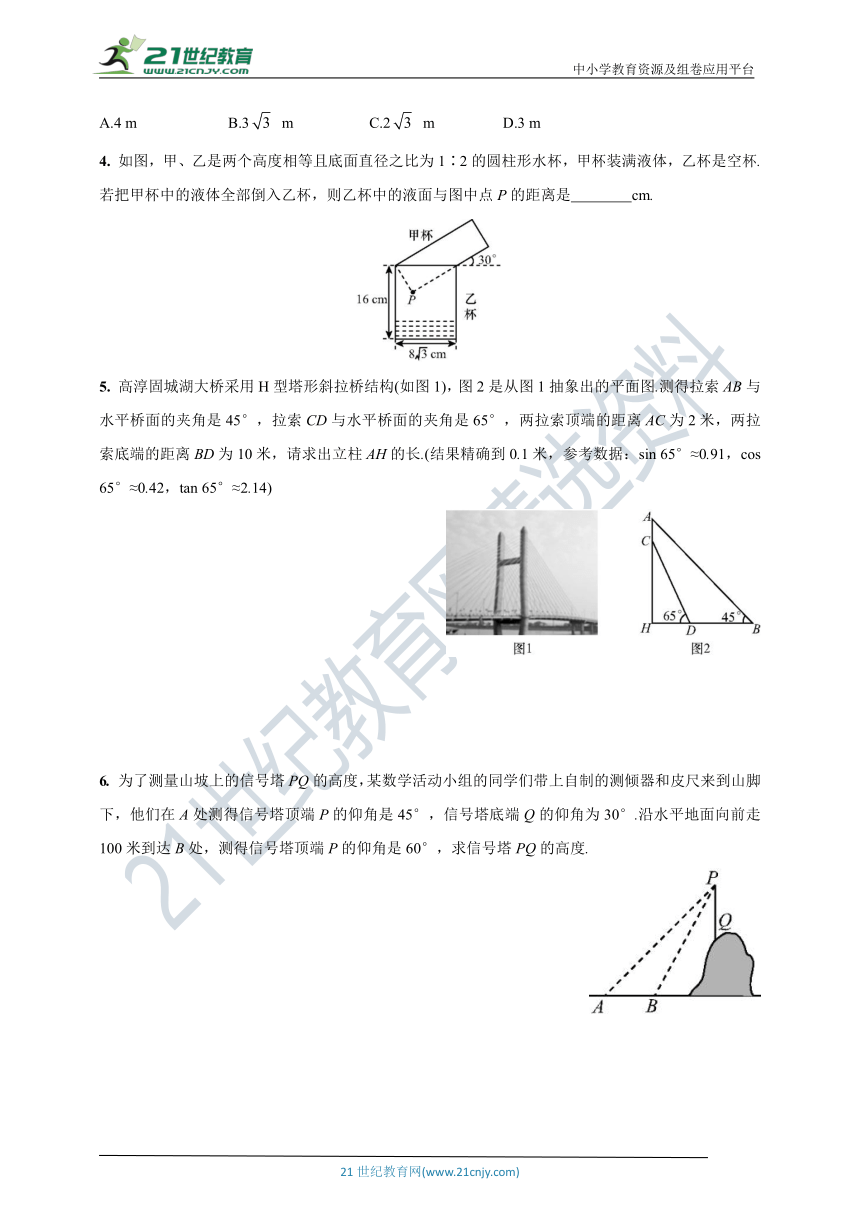
4. 如图,甲、乙是两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是 cm.
5. 高淳固城湖大桥采用H型塔形斜拉桥结构(如图1),图2是从图1抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端的距离BD为10米,请求出立柱AH的长.(结果精确到0.1米,参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
6. 为了测量山坡上的信号塔PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端Q的仰角为30°.沿水平地面向前走100米到达B处,测得信号塔顶端P的仰角是60°,求信号塔PQ的高度.
参 考 答 案
1. C 2. C 3. B
4. 6
5. 解:设AH的长为x米,则CH的长为(x-2)米.在Rt△ABH中,AH=BH·tan 45°,∴BH=x,∴DH=BH-BD=x-10.在Rt△CDH中,CH=DH·tan 65°,∴x-2≈2.14(x-10),解得x≈17.0.答:立柱AH的长约为17.0米.
6. 解:延长PQ交直线AB于点M,连接AQ,∴∠PMA=90°.设PM的长为x米,在Rt△PAM中,∠PAM=45°,∴AM=PM=x米,∴BM=(x-100)米.在Rt△PBM中,∵tan ∠PBM=,∴tan 60°==,解得x=50(3+).在Rt△QAM中,∵tan ∠QAM=,∴QM=AM·tan ∠QAM=50(3+)×tan 30°=50(+1)(米),∴PQ=PM-QM=100(米).答:信号塔PQ的高度约为100米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第1课时 仰角、俯角
1. 如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β.已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asin α+asin β B.acos α+acos β
C.atan α+atan β D.+
2. 如图,为安全起见,游乐园拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 m B.2 m C.3 m D.3 m
3. 如图所示的钓鱼竿AC长6 m,露在水面上的鱼线BC长3 m,钓者想看看鱼钩上的情况,把鱼竿AC逆时针转动15°到AC'的位置,此时露在水面上的鱼线B'C'的长度是( )
A.4 m B.3 m C.2 m D.3 m
4. 如图,甲、乙是两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是 cm.
5. 高淳固城湖大桥采用H型塔形斜拉桥结构(如图1),图2是从图1抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端的距离BD为10米,请求出立柱AH的长.(结果精确到0.1米,参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
6. 为了测量山坡上的信号塔PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端Q的仰角为30°.沿水平地面向前走100米到达B处,测得信号塔顶端P的仰角是60°,求信号塔PQ的高度.
参 考 答 案
1. C 2. C 3. B
4. 6
5. 解:设AH的长为x米,则CH的长为(x-2)米.在Rt△ABH中,AH=BH·tan 45°,∴BH=x,∴DH=BH-BD=x-10.在Rt△CDH中,CH=DH·tan 65°,∴x-2≈2.14(x-10),解得x≈17.0.答:立柱AH的长约为17.0米.
6. 解:延长PQ交直线AB于点M,连接AQ,∴∠PMA=90°.设PM的长为x米,在Rt△PAM中,∠PAM=45°,∴AM=PM=x米,∴BM=(x-100)米.在Rt△PBM中,∵tan ∠PBM=,∴tan 60°==,解得x=50(3+).在Rt△QAM中,∵tan ∠QAM=,∴QM=AM·tan ∠QAM=50(3+)×tan 30°=50(+1)(米),∴PQ=PM-QM=100(米).答:信号塔PQ的高度约为100米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
