苏科版七年级数学下册 第7章平面图形的认识(二) 小结与思考 课件 (共10张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 第7章平面图形的认识(二) 小结与思考 课件 (共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 92.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 20:02:10 | ||
图片预览




文档简介
(共10张PPT)
小结与思考
am·an=am+n
同底数幂相乘,底数 ,指数 .
不变
相加
一同底数幂的乘法
am·an·as=
am+n+s
(m、n、s都是正整数)
(m、n都是正整数)
当我们学了负指数幂之后上面指数不再受正负性的限制.
例.am·a-n=am-n
am·a-n·a-p=
am-n-p
幂的乘方,底数 ,指数 。
幂的乘方运算性质:
积的乘方的运算性质:
(ab)n=_____. (n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
不变
相乘
同底数幂的除法知识点梳理:
1.同底数幂的除法运算性质:
同底数幂相除,
底数不变,指数相减.
am÷an=am–n (m,n为正整数)
2.任何不等于0的数的0次幂等于1.
3.任何不等于0的数的-n次幂,等于这个数的n次幂的倒数.(n是正整数)
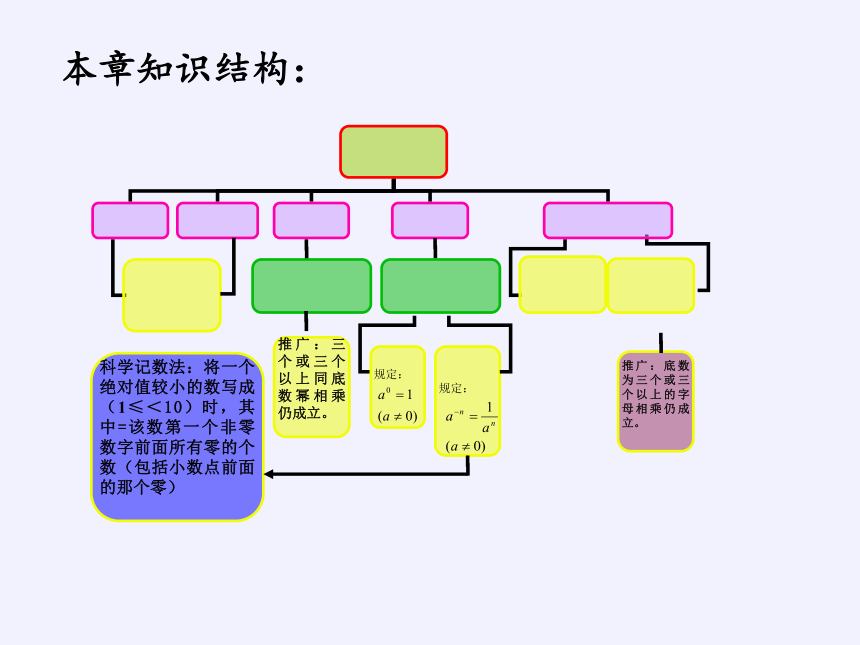
推广:底数为三个或三个以上的字母相乘仍成立。
推广:三个或三个以上同底数幂相乘仍成立。
规定:
规定:
科学记数法:将一个绝对值较小的数写成(1≤<10)时,其中=该数第一个非零数字前面所有零的个数(包括小数点前面的那个零)
本章知识结构:
填空:
(1)若a7·am=a10,则m=______;
(2)若xa·x3=x2a·x2,则a=_______;
(3)a3·____·a2=a3;
用科学记数法表示下列各数.
(1)360000000=____________;
(2)-2730000=_____________;
(3)-0.00000000901=_________;
(4)0.00007008=_____________.
计算
(-2xy2)3
2. (-a2)3.(-a3)2
3. a5.a3+(2a2)4
4. (-2a)3-(-a).(3a)2
5.m19÷m14·m3
6.(-x2y)5÷(-x2y)3
7.(x-y)8÷(x-y)4÷(y-x)3
8.98×272÷(-3)18
1.求m的值:8·22m-1·4m=218.
2.已知am=2,an=3,求(1)a3m+2n.(2)a3m-2n
3.若2x+3·3x+3=36x-2,则x的值是多少
4.若x2n=5,求(3x3n)2-4(x2)2n 的值.
5.比较345与430的大小;
解答题
谢 谢
小结与思考
am·an=am+n
同底数幂相乘,底数 ,指数 .
不变
相加
一同底数幂的乘法
am·an·as=
am+n+s
(m、n、s都是正整数)
(m、n都是正整数)
当我们学了负指数幂之后上面指数不再受正负性的限制.
例.am·a-n=am-n
am·a-n·a-p=
am-n-p
幂的乘方,底数 ,指数 。
幂的乘方运算性质:
积的乘方的运算性质:
(ab)n=_____. (n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
不变
相乘
同底数幂的除法知识点梳理:
1.同底数幂的除法运算性质:
同底数幂相除,
底数不变,指数相减.
am÷an=am–n (m,n为正整数)
2.任何不等于0的数的0次幂等于1.
3.任何不等于0的数的-n次幂,等于这个数的n次幂的倒数.(n是正整数)
推广:底数为三个或三个以上的字母相乘仍成立。
推广:三个或三个以上同底数幂相乘仍成立。
规定:
规定:
科学记数法:将一个绝对值较小的数写成(1≤<10)时,其中=该数第一个非零数字前面所有零的个数(包括小数点前面的那个零)
本章知识结构:
填空:
(1)若a7·am=a10,则m=______;
(2)若xa·x3=x2a·x2,则a=_______;
(3)a3·____·a2=a3;
用科学记数法表示下列各数.
(1)360000000=____________;
(2)-2730000=_____________;
(3)-0.00000000901=_________;
(4)0.00007008=_____________.
计算
(-2xy2)3
2. (-a2)3.(-a3)2
3. a5.a3+(2a2)4
4. (-2a)3-(-a).(3a)2
5.m19÷m14·m3
6.(-x2y)5÷(-x2y)3
7.(x-y)8÷(x-y)4÷(y-x)3
8.98×272÷(-3)18
1.求m的值:8·22m-1·4m=218.
2.已知am=2,an=3,求(1)a3m+2n.(2)a3m-2n
3.若2x+3·3x+3=36x-2,则x的值是多少
4.若x2n=5,求(3x3n)2-4(x2)2n 的值.
5.比较345与430的大小;
解答题
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
