师大金卷高中数学人教A版(2019)必修第二册统计单元测试卷1word版含答案
文档属性
| 名称 | 师大金卷高中数学人教A版(2019)必修第二册统计单元测试卷1word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 706.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 00:00:00 | ||
图片预览



文档简介
必修第二册统计单元测试卷
一、单选题
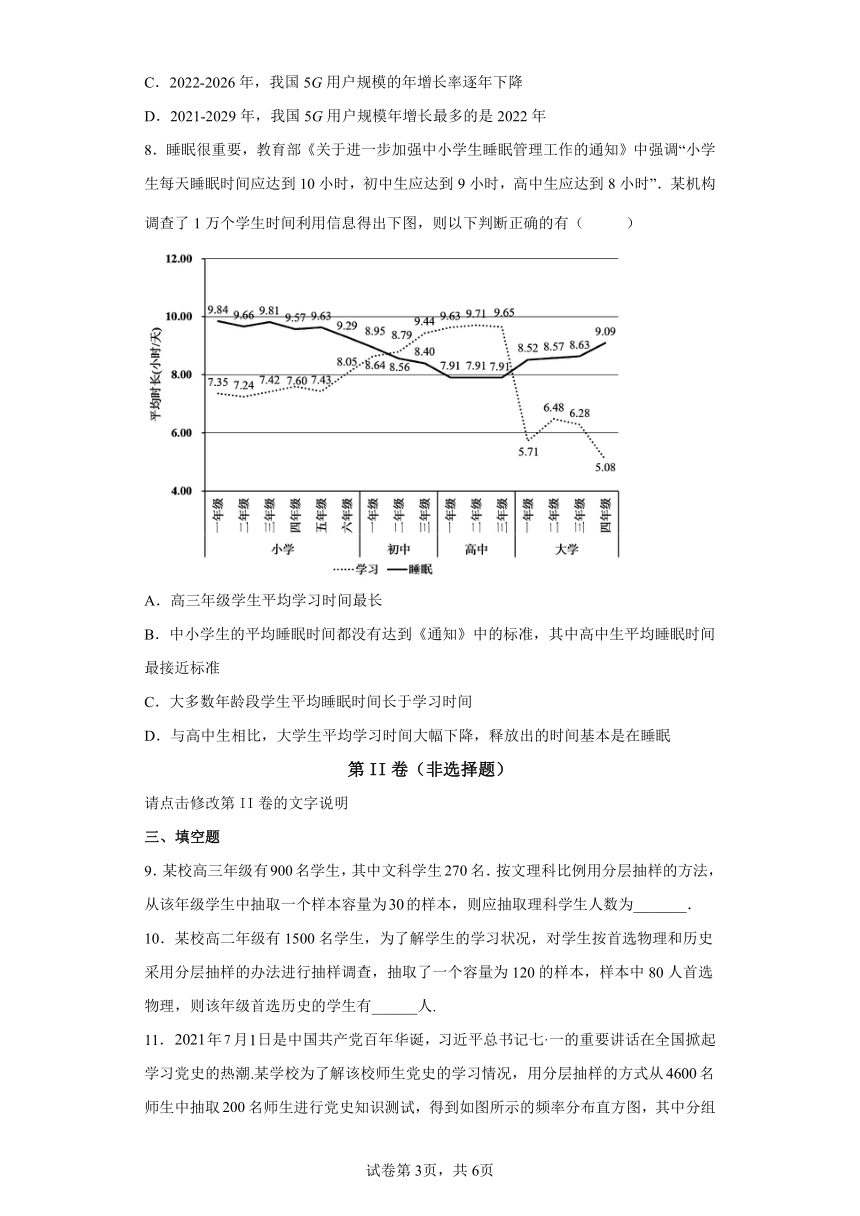
1.如图是民航部门统计的年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高
B.深圳和厦门的春运期间往返机票价格同去年相比有所下降
C.平均价格的涨幅从高到低居于前三位的城市为天津、西安、厦门
D.平均价格从高到低居于前三位的城市为北京、深圳、广州
2.某数学老师记录了班上8名同学的数学考试成绩,得到如下数据:90,98,100,108,111,115,115,125.则这组数据的分位数是( )
A.100 B.111 C.113 D.115
3.某乡镇实现脱贫目标后,在奔小康的道路上,继续大步前进,依托本地区苹果种植的优势,经过3年的发展,苹果总产量翻了一番,统计苹果的品质得到了如下饼图:70,80是指苹果的外径,则以下说法中不正确的是( )
A.80以上优质苹果所占比例增加
B.经过3年的努力,80以上优质苹果产量实现翻了一番的目标
C.70~80的苹果产量翻了一番
D.70以下次品苹果产量减少了一半
4.某次生物实验6个小组的耗材质量(单位:千克)分别为1.71,1.58,1.63,1.43,1.85,1.67,则这组数据的中位数是( )
A.1.63 B.1.67 C.1.64 D.1.65
5.总体由编号01,02,…,29,30的30个个体组成.利用下面的随机数表选取6个个体,选取方法是从如下随机数表的第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
第1行78 16 62 32 08 02 62 42 62 52 53 69 97 28 01 98
第2行32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.19 B.25 C.26 D.27
6.总体编号为01,02,…,29,30的30个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 1572 0802 6315 0216 4319 9714 0198
3204 9234 4936 8200 3623 4869 6938 7181
A.08 B.15 C.16 D.19
二、多选题
7.据新华社报道,“十三五”以来,中国建成了全球规模最大的信息通信网络,光纤宽带用户占比从2015年底的56%提升至94%,行政村通光纤和4G的比例均超过了99%;中国移动网络速率在全球139个国家和地区中排名第4位;在5G网络方面,中国已初步建成全球最大规模的5G移动网络.如图是某科研机构对我国2021-2029年5G用户规模和年增长率发展的预测图,则下列结论正确的是( )
2021—2029年中国5G用户规模和年增长率发展预测图
A.2021-2029年,我国5G用户规模逐年增加
B.2022-2029年,我国5G用户规模后4年的方差小于前4年的方差
C.2022-2026年,我国5G用户规模的年增长率逐年下降
D.2021-2029年,我国5G用户规模年增长最多的是2022年
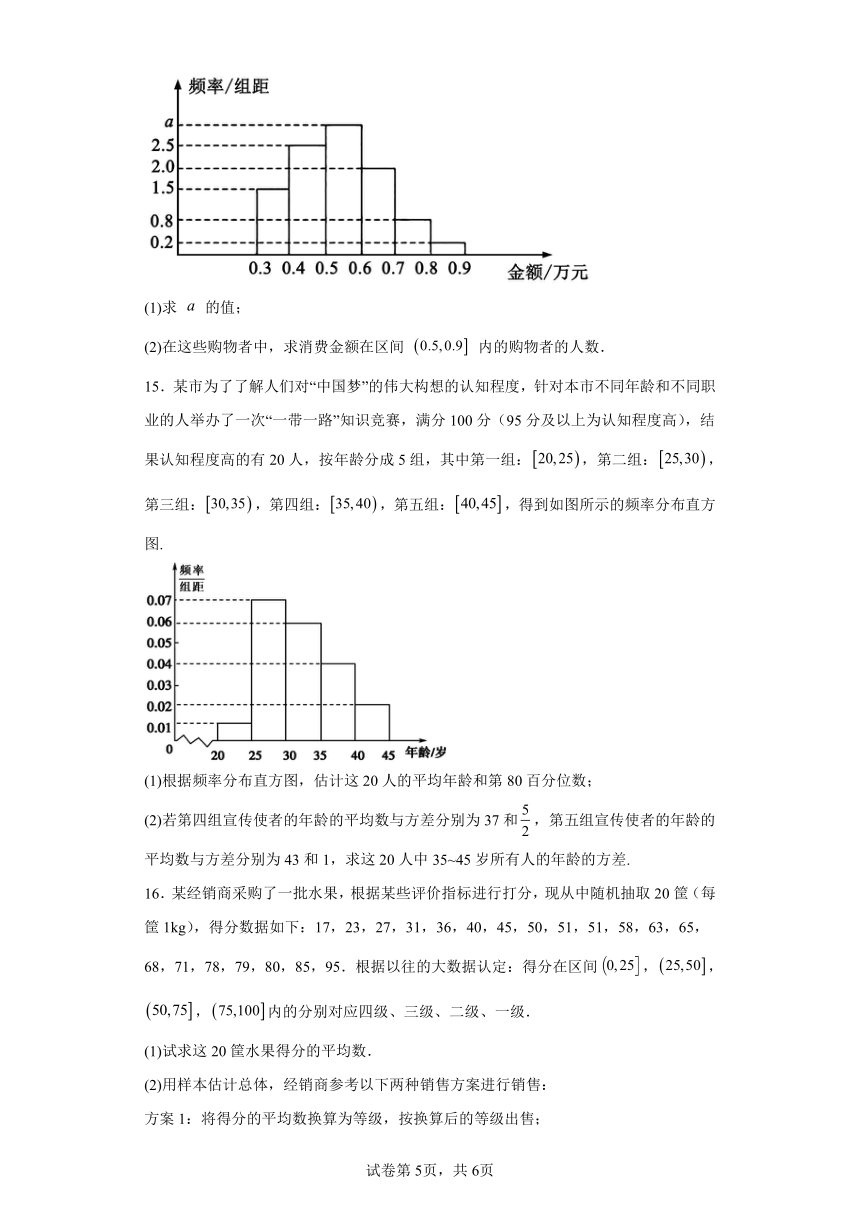
8.睡眠很重要,教育部《关于进一步加强中小学生睡眠管理工作的通知》中强调“小学生每天睡眠时间应达到10小时,初中生应达到9小时,高中生应达到8小时”.某机构调查了1万个学生时间利用信息得出下图,则以下判断正确的有( )
A.高三年级学生平均学习时间最长
B.中小学生的平均睡眠时间都没有达到《通知》中的标准,其中高中生平均睡眠时间最接近标准
C.大多数年龄段学生平均睡眠时间长于学习时间
D.与高中生相比,大学生平均学习时间大幅下降,释放出的时间基本是在睡眠
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.某校高三年级有名学生,其中文科学生名.按文理科比例用分层抽样的方法,从该年级学生中抽取一个样本容量为的样本,则应抽取理科学生人数为_______.
10.某校高二年级有1500名学生,为了解学生的学习状况,对学生按首选物理和历史采用分层抽样的办法进行抽样调查,抽取了一个容量为120的样本,样本中80人首选物理,则该年级首选历史的学生有______人.
11.年月日是中国共产党百年华诞,习近平总书记七·一的重要讲话在全国掀起学习党史的热潮.某学校为了解该校师生党史的学习情况,用分层抽样的方式从名师生中抽取名师生进行党史知识测试,得到如图所示的频率分布直方图,其中分组的区间为,,,,,则名师生测试成绩的中位数是______.(结果保留整数部分)
12.定义一个同学数学成绩优秀的标准为“连续5次数学考试成绩均不低于120分(满分150分)”.现有甲 乙 丙三位同学连续5次数学考试成绩的数据(数据都是正整数)的描述:
①甲同学的5个数据的中位数为125,总体均值为128;
②乙同学的5个数据的中位数为127,众数为121;
③丙同学的5个数据的众数为125,极差为10,总体均值为125.
则数学成绩一定优秀的同学是___________.
四、解答题
13.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
(1)已知样本中分数在[40,50)的学生有5人,试估计总体中分数小于40的人数;
(2)试估计测评成绩的75%分位数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
14.某商品公司随机选取了 1000 名购物者在某年度的消费情况进行统计,并根据消费金 额 (单位: 万元)分成 6 组,制成如下图所示的频率分布直方图:
(1)求 的值;
(2)在这些购物者中,求消费金额在区间 内的购物者的人数.
15.某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有20人,按年龄分成5组,其中第一组:,第二组:,第三组:,第四组:,第五组:,得到如图所示的频率分布直方图.
(1)根据频率分布直方图,估计这20人的平均年龄和第80百分位数;
(2)若第四组宣传使者的年龄的平均数与方差分别为37和,第五组宣传使者的年龄的平均数与方差分别为43和1,求这20人中35~45岁所有人的年龄的方差.
16.某经销商采购了一批水果,根据某些评价指标进行打分,现从中随机抽取20筐(每筐1kg),得分数据如下:17,23,27,31,36,40,45,50,51,51,58,63,65,68,71,78,79,80,85,95.根据以往的大数据认定:得分在区间,,,内的分别对应四级、三级、二级、一级.
(1)试求这20筐水果得分的平均数.
(2)用样本估计总体,经销商参考以下两种销售方案进行销售:
方案1:将得分的平均数换算为等级,按换算后的等级出售;
方案2:分等级出售.
不同等级水果的售价如下表所示:
等级 一级 二级 三级 四级
售价(万元/吨) 2 1.8 1.5 1.2
请从经销商的角度,根据售价分析采用哪种销售方案较好,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
从折线图看涨幅,从条形图看高低,逐项判定即可.
【详解】
从折线图看,深圳的涨幅最接近,从条形图看,北京的平均价格最高,故A正确;
从折线图看,深圳和厦门的涨幅均为负值,故B正确;
从折线图看,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京,故C错误;
从条形图看,平均价格从高到低居于前三位的城市为北京、深圳、广州,故D正确.
故选:C.
2.D
【解析】
【分析】
根据第p百分位数的定义直接计算,再判断作答.
【详解】
由知,这组数据的分位数是按从小到大排列的第6个位置的数,
所以这组数据的分位数是115.
故选:D
3.D
【解析】
【分析】
设原苹果总产量为,从而3年后苹果总产量为;根据饼图,分别计算出3年前和3年后各类苹果的产量,从而可判断选项.
【详解】
设原苹果总产量为,则经过3年的发展,苹果总产量为,
3年前80以上优质苹果所占比例,3年后80以上优质苹果所占比例,所占比例增加,故选项A正确;
3年前80以上优质苹果的产量为,3年后80以上优质苹果的产量为,故80以上优质苹果产量实现翻了一番的目标,选项B正确;
3年前70~80苹果的产量为,3年后70~80苹果的产量为,故70~80的苹果产量翻了一番,选项C正确;
3年前70以下次品苹果的产量为,3年后70以下次品苹果的产量为,故70以下次品苹果的产量没变,选项D错误.
故选:D.
4.D
【解析】
【分析】
将已有数据从小到大排序,根据中位数的定义确定该组数据的中位数.
【详解】
由题设,将数据从小到大排序可得:,
∴中位数为.
故选:D.
5.B
【解析】
【分析】
利用随机数表法列举出样本的前个个体的编号,由此可得出结论.
【详解】
由随机数表法可知,样本的前个个体的编号分别为、、、、,
因此,选出的第个个体的编号为.
故选:B
6.D
【解析】
【分析】
直接根据随机数表依次选取,遇到超出范围或重复的数据要丢弃
【详解】
随机数表第1行的第5列和第6列数字为15,则选取的5个个体依次为:15,08,02,16,19
故选出来的第5个个体的编号为19
故选:D
7.ABC
【解析】
【分析】
根据预测图对选项进行分析,由此确定正确选项.
【详解】
由题图可知,2021-2029年,我国5G用户规模逐年增加,故A正确;
2022-2029年,我国5G用户规模前4年比后4年的分散,方差比后4年的大,故B正确;
2022-2026年,我国5G用户规模的年增长率逐年下降,故C正确;
2021-2029年,我国5G用户规模年增长最多的是2023年,增加了37 499.9万人,而2022年我国5G用户规模增加了20 498.1万人,所以D错误.
故选:ABC
8.BC
【解析】
【分析】
根据图象提供数据对选项进行分析,从而确定正确答案.
【详解】
根据图象可知,高三年级学生平均学习时间没有高二年级学生平均学习时间长,A选项错误.
根据图象可知,中小学生平均睡眠时间都没有达到《通知》中的标准,高中生平均睡眠时间最接近标准,B选项正确.
学习时间大于睡眠时间的有:初二、初三、高一、高二、高三,占比.睡眠时间长于学习时间的占比,C选项正确.
从高三到大学一年级,学习时间减少,睡眠时间增加,所以D选项错误.
故选:BC
9.
【解析】
【分析】
根据分层抽样可计算出抽取理科学生人数.
【详解】
设应抽取理科学生人数为,则,解得.
故答案为:.
10.500
【解析】
【分析】
根据分层抽样的定义进行求解.
【详解】
解:根据题意抽取的120人中有人选历史.
设该年级首选历史的学生有人,则,解得.
故答案为:500
11.
【解析】
【分析】
利用中位数左边的矩形面积之和为可列等式求出中位数的值.
【详解】
由频率分布直方图知前三组频率之和,
前四组频率之和,
所以中位数在第四组,设中位数为,则,解得.
故答案为:.
12.乙
【解析】
【分析】
根据中位数、均值、众数、极差等概念,找出满足条件的5个数,看最小的能否小于120即可判断.
【详解】
在①中,甲同学的5个数据的中位数为125,总体均值为128,
可以找到很多反例,如118,119,125,128,150,故甲同学的数学成绩不一定优秀;
在②中,乙同学的5个数据的中位数为127,众数为121,
所以前三个数为121,121,127,则后两个数肯定大于127,故乙同学的数学成绩一定优秀;
在③中,丙同学的5个数据的众数为125,极差为10,总体均值为125,最大值与最小值的差为10,若最大值为129,则最小值为119.即119,125,125,127,129,故丙同学的数学成绩不一定优秀.
综上,数学成绩一定优秀的同学只有乙.
故答案为:乙.
13.(1)20人
(2)
(3)
【解析】
【分析】
(1)根据频率分布直方图先求出样本中分数在[40,90)的频率,即可解出;
(2)先根据频率分布直方图判断出75%分位数在[70,80)之间,即可根据分位数公式算出;
(3)根据频率分布直方图知分数不小于70分的人数中男女各占30人,从而可知样本中男生有60人,女生有40人,即可求出总体中男生和女生人数的比例.
(1)
由频率分布直方图知,分数在[50,90)的频率为(0.01+0.02+0.04+0.02)×10=0.9,在样本中分数在[50,90)的人数为100×0.9=90(人),在样本中分数在[40,90)的人数为95人,所以分数在[40,90)的人数为400×0.95=380(人),总体中分数小于40的人数为20人
(2)
测试成绩从低到高排序,占人数75%的人分数在[70,80)之间,所以估计测评成绩的75%分位数为
(3)
由频率分布直方图知,分数不小于70分的人数共有60人,由已知男女各占30人,从而样本中男生有60人,女生有40人,故总体中男生与女生的比例为.
14.(1)
(2)600人
【解析】
【分析】
(1)根据频率分布直方图的性质,各小矩形的面积之和为,即可求出;
(2)先由频率分布直方图可求出消费金额在区间内的频率,再根据频数=频率样本容量,即可得到购物者的人数.
(1)
由频率分布直方图及频率和等于1可得:
,解得.
(2)
消费金额在区间内的频率为,
所以消费金额在区间内的购物者的人数为人.
15.(1)32.25,第80百分位数为37.5
(2)10
【解析】
【分析】
(1)直接根据频率分布直方图计算平均数和百分位数;
(2)利用分层抽样得第四组和第五组分别抽取人和人,进而设第四组、第五组的宣传使者的年龄的平均数分别为,,方差分别为,,第四组和第五组所有宣传使者的年龄平均数为,方差为,进而根据方差公式,代入计算即可得答案.
(1)
设这20人的平均年龄为,则
.
设第80百分位数为,由,解得.
(2)
由频率分布直方图得各组人数之比为,
故各组中采用分层随机抽样的方法抽取20人,第四组和第五组分别抽取人和人,
设第四组、第五组的宣传使者的年龄的平均数分别为,,方差分别为,,
则,,,,
设第四组和第五组所有宣传使者的年龄平均数为,方差为.
则,,
因此,第四组和第五组所有宣传使者的年龄方差为10,
据此,可估计这人中年龄在35~45岁的所有人的年龄方差约为10.
16.(1)55.65
(2)采用方案1较好,理由见解析
【解析】
【分析】
(1)直接利用平均数的计算公式即可求解;
(2)分别计算出这两种方案的单价,进行比较,即可下结论.
(1)
这20筐水果得分的平均数为
.
(2)
方案1:由于得分的平均数,
所以可以估计这批水果的销售单价为1.8万元/吨.
方案2:设这批水果售价的平均值为万元/吨,由已知数据得,
得分在内的有17,23,共2个,所以估计四级水果所占比例为,
得分在内的有27,31,36,40,45,50,共6个,所以估计三级水果所占比例为,
得分在内的有51,51,58,63,65,68,71,共7个,所以估计二级水果所占比例为,
得分在内的有78,79,80,85,95,共5个,所以估计一级水果所占比例为,
则(万元/吨).
所以从经销商的角度考虑,采用方案1的售价较高,所以采用方案1较好
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图是民航部门统计的年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高
B.深圳和厦门的春运期间往返机票价格同去年相比有所下降
C.平均价格的涨幅从高到低居于前三位的城市为天津、西安、厦门
D.平均价格从高到低居于前三位的城市为北京、深圳、广州
2.某数学老师记录了班上8名同学的数学考试成绩,得到如下数据:90,98,100,108,111,115,115,125.则这组数据的分位数是( )
A.100 B.111 C.113 D.115
3.某乡镇实现脱贫目标后,在奔小康的道路上,继续大步前进,依托本地区苹果种植的优势,经过3年的发展,苹果总产量翻了一番,统计苹果的品质得到了如下饼图:70,80是指苹果的外径,则以下说法中不正确的是( )
A.80以上优质苹果所占比例增加
B.经过3年的努力,80以上优质苹果产量实现翻了一番的目标
C.70~80的苹果产量翻了一番
D.70以下次品苹果产量减少了一半
4.某次生物实验6个小组的耗材质量(单位:千克)分别为1.71,1.58,1.63,1.43,1.85,1.67,则这组数据的中位数是( )
A.1.63 B.1.67 C.1.64 D.1.65
5.总体由编号01,02,…,29,30的30个个体组成.利用下面的随机数表选取6个个体,选取方法是从如下随机数表的第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
第1行78 16 62 32 08 02 62 42 62 52 53 69 97 28 01 98
第2行32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.19 B.25 C.26 D.27
6.总体编号为01,02,…,29,30的30个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 1572 0802 6315 0216 4319 9714 0198
3204 9234 4936 8200 3623 4869 6938 7181
A.08 B.15 C.16 D.19
二、多选题
7.据新华社报道,“十三五”以来,中国建成了全球规模最大的信息通信网络,光纤宽带用户占比从2015年底的56%提升至94%,行政村通光纤和4G的比例均超过了99%;中国移动网络速率在全球139个国家和地区中排名第4位;在5G网络方面,中国已初步建成全球最大规模的5G移动网络.如图是某科研机构对我国2021-2029年5G用户规模和年增长率发展的预测图,则下列结论正确的是( )
2021—2029年中国5G用户规模和年增长率发展预测图
A.2021-2029年,我国5G用户规模逐年增加
B.2022-2029年,我国5G用户规模后4年的方差小于前4年的方差
C.2022-2026年,我国5G用户规模的年增长率逐年下降
D.2021-2029年,我国5G用户规模年增长最多的是2022年
8.睡眠很重要,教育部《关于进一步加强中小学生睡眠管理工作的通知》中强调“小学生每天睡眠时间应达到10小时,初中生应达到9小时,高中生应达到8小时”.某机构调查了1万个学生时间利用信息得出下图,则以下判断正确的有( )
A.高三年级学生平均学习时间最长
B.中小学生的平均睡眠时间都没有达到《通知》中的标准,其中高中生平均睡眠时间最接近标准
C.大多数年龄段学生平均睡眠时间长于学习时间
D.与高中生相比,大学生平均学习时间大幅下降,释放出的时间基本是在睡眠
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.某校高三年级有名学生,其中文科学生名.按文理科比例用分层抽样的方法,从该年级学生中抽取一个样本容量为的样本,则应抽取理科学生人数为_______.
10.某校高二年级有1500名学生,为了解学生的学习状况,对学生按首选物理和历史采用分层抽样的办法进行抽样调查,抽取了一个容量为120的样本,样本中80人首选物理,则该年级首选历史的学生有______人.
11.年月日是中国共产党百年华诞,习近平总书记七·一的重要讲话在全国掀起学习党史的热潮.某学校为了解该校师生党史的学习情况,用分层抽样的方式从名师生中抽取名师生进行党史知识测试,得到如图所示的频率分布直方图,其中分组的区间为,,,,,则名师生测试成绩的中位数是______.(结果保留整数部分)
12.定义一个同学数学成绩优秀的标准为“连续5次数学考试成绩均不低于120分(满分150分)”.现有甲 乙 丙三位同学连续5次数学考试成绩的数据(数据都是正整数)的描述:
①甲同学的5个数据的中位数为125,总体均值为128;
②乙同学的5个数据的中位数为127,众数为121;
③丙同学的5个数据的众数为125,极差为10,总体均值为125.
则数学成绩一定优秀的同学是___________.
四、解答题
13.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
(1)已知样本中分数在[40,50)的学生有5人,试估计总体中分数小于40的人数;
(2)试估计测评成绩的75%分位数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
14.某商品公司随机选取了 1000 名购物者在某年度的消费情况进行统计,并根据消费金 额 (单位: 万元)分成 6 组,制成如下图所示的频率分布直方图:
(1)求 的值;
(2)在这些购物者中,求消费金额在区间 内的购物者的人数.
15.某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有20人,按年龄分成5组,其中第一组:,第二组:,第三组:,第四组:,第五组:,得到如图所示的频率分布直方图.
(1)根据频率分布直方图,估计这20人的平均年龄和第80百分位数;
(2)若第四组宣传使者的年龄的平均数与方差分别为37和,第五组宣传使者的年龄的平均数与方差分别为43和1,求这20人中35~45岁所有人的年龄的方差.
16.某经销商采购了一批水果,根据某些评价指标进行打分,现从中随机抽取20筐(每筐1kg),得分数据如下:17,23,27,31,36,40,45,50,51,51,58,63,65,68,71,78,79,80,85,95.根据以往的大数据认定:得分在区间,,,内的分别对应四级、三级、二级、一级.
(1)试求这20筐水果得分的平均数.
(2)用样本估计总体,经销商参考以下两种销售方案进行销售:
方案1:将得分的平均数换算为等级,按换算后的等级出售;
方案2:分等级出售.
不同等级水果的售价如下表所示:
等级 一级 二级 三级 四级
售价(万元/吨) 2 1.8 1.5 1.2
请从经销商的角度,根据售价分析采用哪种销售方案较好,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
从折线图看涨幅,从条形图看高低,逐项判定即可.
【详解】
从折线图看,深圳的涨幅最接近,从条形图看,北京的平均价格最高,故A正确;
从折线图看,深圳和厦门的涨幅均为负值,故B正确;
从折线图看,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京,故C错误;
从条形图看,平均价格从高到低居于前三位的城市为北京、深圳、广州,故D正确.
故选:C.
2.D
【解析】
【分析】
根据第p百分位数的定义直接计算,再判断作答.
【详解】
由知,这组数据的分位数是按从小到大排列的第6个位置的数,
所以这组数据的分位数是115.
故选:D
3.D
【解析】
【分析】
设原苹果总产量为,从而3年后苹果总产量为;根据饼图,分别计算出3年前和3年后各类苹果的产量,从而可判断选项.
【详解】
设原苹果总产量为,则经过3年的发展,苹果总产量为,
3年前80以上优质苹果所占比例,3年后80以上优质苹果所占比例,所占比例增加,故选项A正确;
3年前80以上优质苹果的产量为,3年后80以上优质苹果的产量为,故80以上优质苹果产量实现翻了一番的目标,选项B正确;
3年前70~80苹果的产量为,3年后70~80苹果的产量为,故70~80的苹果产量翻了一番,选项C正确;
3年前70以下次品苹果的产量为,3年后70以下次品苹果的产量为,故70以下次品苹果的产量没变,选项D错误.
故选:D.
4.D
【解析】
【分析】
将已有数据从小到大排序,根据中位数的定义确定该组数据的中位数.
【详解】
由题设,将数据从小到大排序可得:,
∴中位数为.
故选:D.
5.B
【解析】
【分析】
利用随机数表法列举出样本的前个个体的编号,由此可得出结论.
【详解】
由随机数表法可知,样本的前个个体的编号分别为、、、、,
因此,选出的第个个体的编号为.
故选:B
6.D
【解析】
【分析】
直接根据随机数表依次选取,遇到超出范围或重复的数据要丢弃
【详解】
随机数表第1行的第5列和第6列数字为15,则选取的5个个体依次为:15,08,02,16,19
故选出来的第5个个体的编号为19
故选:D
7.ABC
【解析】
【分析】
根据预测图对选项进行分析,由此确定正确选项.
【详解】
由题图可知,2021-2029年,我国5G用户规模逐年增加,故A正确;
2022-2029年,我国5G用户规模前4年比后4年的分散,方差比后4年的大,故B正确;
2022-2026年,我国5G用户规模的年增长率逐年下降,故C正确;
2021-2029年,我国5G用户规模年增长最多的是2023年,增加了37 499.9万人,而2022年我国5G用户规模增加了20 498.1万人,所以D错误.
故选:ABC
8.BC
【解析】
【分析】
根据图象提供数据对选项进行分析,从而确定正确答案.
【详解】
根据图象可知,高三年级学生平均学习时间没有高二年级学生平均学习时间长,A选项错误.
根据图象可知,中小学生平均睡眠时间都没有达到《通知》中的标准,高中生平均睡眠时间最接近标准,B选项正确.
学习时间大于睡眠时间的有:初二、初三、高一、高二、高三,占比.睡眠时间长于学习时间的占比,C选项正确.
从高三到大学一年级,学习时间减少,睡眠时间增加,所以D选项错误.
故选:BC
9.
【解析】
【分析】
根据分层抽样可计算出抽取理科学生人数.
【详解】
设应抽取理科学生人数为,则,解得.
故答案为:.
10.500
【解析】
【分析】
根据分层抽样的定义进行求解.
【详解】
解:根据题意抽取的120人中有人选历史.
设该年级首选历史的学生有人,则,解得.
故答案为:500
11.
【解析】
【分析】
利用中位数左边的矩形面积之和为可列等式求出中位数的值.
【详解】
由频率分布直方图知前三组频率之和,
前四组频率之和,
所以中位数在第四组,设中位数为,则,解得.
故答案为:.
12.乙
【解析】
【分析】
根据中位数、均值、众数、极差等概念,找出满足条件的5个数,看最小的能否小于120即可判断.
【详解】
在①中,甲同学的5个数据的中位数为125,总体均值为128,
可以找到很多反例,如118,119,125,128,150,故甲同学的数学成绩不一定优秀;
在②中,乙同学的5个数据的中位数为127,众数为121,
所以前三个数为121,121,127,则后两个数肯定大于127,故乙同学的数学成绩一定优秀;
在③中,丙同学的5个数据的众数为125,极差为10,总体均值为125,最大值与最小值的差为10,若最大值为129,则最小值为119.即119,125,125,127,129,故丙同学的数学成绩不一定优秀.
综上,数学成绩一定优秀的同学只有乙.
故答案为:乙.
13.(1)20人
(2)
(3)
【解析】
【分析】
(1)根据频率分布直方图先求出样本中分数在[40,90)的频率,即可解出;
(2)先根据频率分布直方图判断出75%分位数在[70,80)之间,即可根据分位数公式算出;
(3)根据频率分布直方图知分数不小于70分的人数中男女各占30人,从而可知样本中男生有60人,女生有40人,即可求出总体中男生和女生人数的比例.
(1)
由频率分布直方图知,分数在[50,90)的频率为(0.01+0.02+0.04+0.02)×10=0.9,在样本中分数在[50,90)的人数为100×0.9=90(人),在样本中分数在[40,90)的人数为95人,所以分数在[40,90)的人数为400×0.95=380(人),总体中分数小于40的人数为20人
(2)
测试成绩从低到高排序,占人数75%的人分数在[70,80)之间,所以估计测评成绩的75%分位数为
(3)
由频率分布直方图知,分数不小于70分的人数共有60人,由已知男女各占30人,从而样本中男生有60人,女生有40人,故总体中男生与女生的比例为.
14.(1)
(2)600人
【解析】
【分析】
(1)根据频率分布直方图的性质,各小矩形的面积之和为,即可求出;
(2)先由频率分布直方图可求出消费金额在区间内的频率,再根据频数=频率样本容量,即可得到购物者的人数.
(1)
由频率分布直方图及频率和等于1可得:
,解得.
(2)
消费金额在区间内的频率为,
所以消费金额在区间内的购物者的人数为人.
15.(1)32.25,第80百分位数为37.5
(2)10
【解析】
【分析】
(1)直接根据频率分布直方图计算平均数和百分位数;
(2)利用分层抽样得第四组和第五组分别抽取人和人,进而设第四组、第五组的宣传使者的年龄的平均数分别为,,方差分别为,,第四组和第五组所有宣传使者的年龄平均数为,方差为,进而根据方差公式,代入计算即可得答案.
(1)
设这20人的平均年龄为,则
.
设第80百分位数为,由,解得.
(2)
由频率分布直方图得各组人数之比为,
故各组中采用分层随机抽样的方法抽取20人,第四组和第五组分别抽取人和人,
设第四组、第五组的宣传使者的年龄的平均数分别为,,方差分别为,,
则,,,,
设第四组和第五组所有宣传使者的年龄平均数为,方差为.
则,,
因此,第四组和第五组所有宣传使者的年龄方差为10,
据此,可估计这人中年龄在35~45岁的所有人的年龄方差约为10.
16.(1)55.65
(2)采用方案1较好,理由见解析
【解析】
【分析】
(1)直接利用平均数的计算公式即可求解;
(2)分别计算出这两种方案的单价,进行比较,即可下结论.
(1)
这20筐水果得分的平均数为
.
(2)
方案1:由于得分的平均数,
所以可以估计这批水果的销售单价为1.8万元/吨.
方案2:设这批水果售价的平均值为万元/吨,由已知数据得,
得分在内的有17,23,共2个,所以估计四级水果所占比例为,
得分在内的有27,31,36,40,45,50,共6个,所以估计三级水果所占比例为,
得分在内的有51,51,58,63,65,68,71,共7个,所以估计二级水果所占比例为,
得分在内的有78,79,80,85,95,共5个,所以估计一级水果所占比例为,
则(万元/吨).
所以从经销商的角度考虑,采用方案1的售价较高,所以采用方案1较好
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
