师大金卷高中数学人教A版(2019)必修第二册统计单元测试卷3word版含答案
文档属性
| 名称 | 师大金卷高中数学人教A版(2019)必修第二册统计单元测试卷3word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 452.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 00:00:00 | ||
图片预览




文档简介
必修第二册统计单元测试卷
一、单选题
1.某班对期中成绩进行分析,利用随机数表法抽取样本时,先将60个同学的成绩按01,02,03,……,60进行编号,然后从随机数表第9行第5列的数1开始向右读,则选出的第6个个体是( )
(注:如下为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58
33 21 12 34 29 78 64 56 07 82 52 45 07 44 38 15 51 00 13
A.07 B.25 C.42 D.52
2.电子元件,使用寿命时间统计如茎叶图所示,下列说法正确的是( )
A.,两电子元件使用时间的极差相等
B.电子元件使用时间的中位数比小
C.电子元件使用时间众数与中位数相等
D.,两电子元件使用时间的平均数相等
3.某班进行了一次数学测试,全班学生的成绩都落在区间内,其成绩的频率分布直方图如图所示,若该班学生这次数学测试成绩的中位数的估计值为,则的值为( )
A. B. C. D.
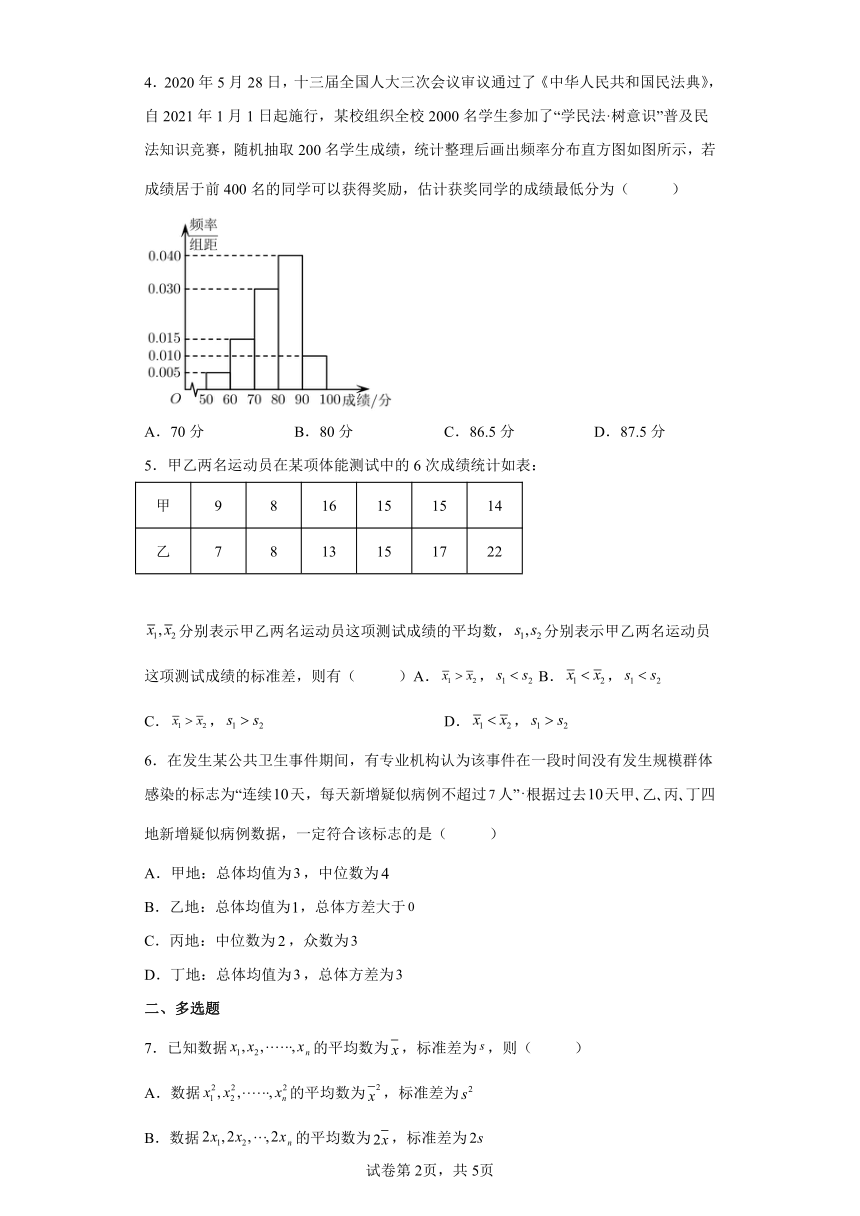
4.2020年5月28日,十三届全国人大三次会议审议通过了《中华人民共和国民法典》,自2021年1月1日起施行,某校组织全校2000名学生参加了“学民法·树意识”普及民法知识竞赛,随机抽取200名学生成绩,统计整理后画出频率分布直方图如图所示,若成绩居于前400名的同学可以获得奖励,估计获奖同学的成绩最低分为( )
A.70分 B.80分 C.86.5分 D.87.5分
5.甲乙两名运动员在某项体能测试中的6次成绩统计如表:
甲 9 8 16 15 15 14
乙 7 8 13 15 17 22
分别表示甲乙两名运动员这项测试成绩的平均数,分别表示甲乙两名运动员这项测试成绩的标准差,则有( )A., B.,
C., D.,
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生规模群体感染的标志为“连续天,每天新增疑似病例不超过人”根据过去天甲 乙 丙 丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为,中位数为
B.乙地:总体均值为,总体方差大于
C.丙地:中位数为,众数为
D.丁地:总体均值为,总体方差为
二、多选题
7.已知数据的平均数为,标准差为,则( )
A.数据的平均数为,标准差为
B.数据的平均数为,标准差为
C.数据的平均数为,方差为
D.数据的平均数为,方差为
8.有一组样本数据,另一组样本数据,其中,c为非零常数,则( )
A.两组样本数据平均数相同 B.两组样本数据与各自平均数的“平均距离”相等
C.两组样本数据方差相同 D.两组样本数据极差相同
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.已知某高级中学高一 高二 高三三个年级的学生人数分别为880人 860人 820人,现用分层抽样方法从该校三个年级抽出128人参加社会实践活动问卷调查,则在高二年级抽出的人数为___________.
10.已知某样本数据分别为1,4,3,a,6,且样本均值,则样本方差_________.
11.某学校在校学生有2000人,为了增强学生的体质,学校举行了跑步和登山比赛,每人都参加且只参加其中一项比赛,高一、高二、高三年级参加跑步的人数分别为a,b,c,且,全校参加登山的人数占总人数的.为了了解学生对本次比赛的满意程度,按分层抽样的方法从中抽取一个容量为200的样本进行调查,则应从高三年级参加跑步的学生中抽取人数为______.
12.已知一组数据4,,,5,7的平均数为4,则这组数的方差是________.
四、解答题
13.某样本由个数组成,平均数为,方差为.这个样本可分为两层:第一层有m个数,分别为,,…,,平均数为,方差为;第二层有n个数,分别为,,…,,平均数为,方差为.
(1)证明:;
(2)证明:,;
(3)证明:.
14.随着新冠肺炎疫情的稳定,各地的经济均呈现缓慢的恢复趋势,为了更进一步做好疫情的防控工作,避免疫情的再度爆发,A地区规定居民出行或者出席公共场合均需佩戴口罩,现将A地区20000个居民一周的口罩使用个数统计如下表所示,其中每周的口罩使用个数在6以上(含6)的有14000人.
口罩使用数量
频率 0.2 m 0.3 n 0.1
(1)求m,n的值;
(2)根据表中数据,完善上面的频率分布直方图;
(3)计算A地区居民一周口罩使用个数的平均数以及方差.
15.在下列项目中选择适当的问题,对你所收集的数据确定一个标题,明确需要解决的问题,并说明数据的收集方法与数据处理 分析的方法和过程.
(1)某项体育比赛的成绩记录;
(2)天气报告——温度 雨量 湿度 暴风雨;
(3)交通运输记录——事故 运输量 车辆数 停车场的数量;
(4)商业状况——销售额 价格 银行存款 利率;
(5)校服的款式 颜色;
(6)看电视 看电影,借阅图书杂志.
16.中医药文化历史悠久.我国经历了数千年的艰难探索和发展,逐渐积淀成博大精深的中医药文化.某医药采购商计划从云南昭通购买500千克乌天麻,购买数据如下表:
乌天麻规格 (支/千克)
数量(千克) 200 100 150 50
(1)估计每千克乌天麻的平均支数(同一组中的数据用该区间的中点值作代表);
(2)已知生产商提供该产品的两种销售方案供采购商选择,
方案一:这500千克乌天麻一律售价为280元/千克.
方案二:这500千克按规格不同售出,其售价如下:
乌天麻规格 (支/千克)
售价(元/千克) 300 280 260 240
从采购商的角度考虑,应该选择哪种方案 请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
从指定位置起依次读两位数码,超出编号的数删除.
【详解】
根据题意,从随机数表第9行第5列的数1开始向右读,
依次选出的号码数是:12,34,29,56,07,52;
所以第6个个体是52.
故选:D.
2.C
【解析】
【分析】
根据茎叶图即可判断各选项的真假.
【详解】
对A ,的极差是,的极差是,两者不相等,故A选项错误;
对B ,的中位数是,的中位数是55,故的中位数较小,故B选项错误;
对C ,的众数为55,与中位数相同,故C选项正确;
对D ,的平均数是49.9,的平均数是52.9,不相等,故D选项错误.
故选:C.
3.A
【解析】
【分析】
根据已知条件可得出关于、的方程组,解出这两个量的值,即可求得结果.
【详解】
由题意有,得,
又由,得,
解得,,有.
故选:A.
4.D
【解析】
【分析】
根据频率分布直方图求出第i组的频率为,设获奖的最低分为a,由题意列方程求出即可.
【详解】
设频率分布直方图第i组的频率为,则
.
全校2000名学生中前400名的同学可以获得奖励,所以获奖同学的概率为,
故获奖的最低分落在区间.设获奖的最低分为a,则:
,
解得:.
故选:D
5.B
【解析】
【分析】
根据给定统计表计算、,再比较、大小判断作答.
【详解】
依题意,,,
,
,
所以,.
故选:B
6.D
【解析】
【分析】
利用平均数、中位数、方差的计算公式以及含义,对四个选项逐一分析判断即可.
【详解】
因为平均数和中位数不能限制某一天的病例超过人,故A不正确;
乙地:总体均值为,说明乙地过去天新增疑似病例例,
总体方差大于,有可能存在一天新增疑似病例超过人,故B不正确;
中位数和众数也不能限制某一天的病例超过人,故C不正确;
当总体平均数是,若有一个数据超过,则方差就超过,故D正确,
故选:D.
7.BC
【解析】
【分析】
根据平均数、方差、标准差的定义逐项判断可得答案.
【详解】
, ,
对于A,与不存在关系,不一定相等,故错误;
对于B,,,所以数据的标准差为,故正确;
对于C,,,故正确;
对于D,数据的平均数为,方差为
,故错误.
故选:BC.
8.BCD
【解析】
【分析】
根据题意,结合平均数、方差、极差、“平均距离”的计算公式,一一判断即可.
【详解】
对于选项A, ,,故A错;
对于选项B, ,,故B正确;
对于选项C,,,故C正确;
对于选项D,,故D正确.
故选:BCD.
9.43
【解析】
【分析】
求出抽样比可得答案.
【详解】
由题意可知,在高二年级中抽调的人数为(人).
故答案为:43.
10.##
【解析】
【分析】
先求得的值,然后求得样本方差.
【详解】
依题意,
所以.
故答案为:
11.
【解析】
【分析】
由题意求得样本中抽取的高三的人数为人进而求得样本中高三年级参加登山的人,即可求解.
【详解】
由题意,高一、高二、高三年级参加跑步的人数分别为a,b,c,且,
所以样本中抽取的高三的人数为人,
又因为全校参加登山的人数占总人数的,
所以样本中高三年级参加登山的人数为,
所以样本中高三年级参加跑步的人数为人.
故答案为:.
12.3.6
【解析】
【分析】
先根据这组数据的平均数为4,求得a,再利用方差公式求解.
【详解】
因为一组数据4,,,5,7的平均数为4,
所以,
解得,
所以这组数据为,
所以这组数据的方差为
故答案为:3.6
13.(1)证明见解析;
(2)证明见解析;
(3)证明见解析.
【解析】
【分析】
(1)利用平均数的定义及计算公式即证;
(2)利用平均数的含义及计算公式即证;
(3)利用平均数、方差的定义及计算公式即证;
(1)
根据平均数定义,,
故,
因此.
(2)
因为,,
所以.
因为,,
所以
.
(3)
方法一:由方差定义可得,由(2)可知,
所以
.
同理,于是
将代入化简得.
方法二:由题设,所以
.
同理,于是
将代入化简得.
14.(1),;
(2)频率分布直方图见解析;
(3)平均数是7,方差是.
【解析】
【分析】
(1)由每周的口罩使用个数在6以上(含6)的有14000人求出6以上(含6)的频率,从而可得值,同样由6个以下的频率求得;
(2)根据频率表作出频率分布直方图;
(3)由每组数据中点值乘以频率相加得平均值,由每组数据中点值减去平均值后平方再乘以频率相加得方差.
(1)
由已知,;
(2)
频率分布直方图如下:
(3)
由频率分布直方图得
一周内使用口罩的平均数为
,
方差为.
15.(1)
(2)
(3)
(4)
(5)
(6)
【解析】
略
16.(1)16支
(2)选择方案二,理由见解析
【解析】
【分析】
(1)根据频率分布表,利用平均数公式求解;
(2)根据频率分布表,利用平均数公式求得方案二的产品的平均售价,再比较下结论.
(1)
解:,
所以该采购商购买的乌天麻每千克的平均支数为16支.
(2)
由题意知:方案二的产品的平均售价为:
(元/千克).
因为278<280,所以从采购商的角度考虑,选择方案二.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某班对期中成绩进行分析,利用随机数表法抽取样本时,先将60个同学的成绩按01,02,03,……,60进行编号,然后从随机数表第9行第5列的数1开始向右读,则选出的第6个个体是( )
(注:如下为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58
33 21 12 34 29 78 64 56 07 82 52 45 07 44 38 15 51 00 13
A.07 B.25 C.42 D.52
2.电子元件,使用寿命时间统计如茎叶图所示,下列说法正确的是( )
A.,两电子元件使用时间的极差相等
B.电子元件使用时间的中位数比小
C.电子元件使用时间众数与中位数相等
D.,两电子元件使用时间的平均数相等
3.某班进行了一次数学测试,全班学生的成绩都落在区间内,其成绩的频率分布直方图如图所示,若该班学生这次数学测试成绩的中位数的估计值为,则的值为( )
A. B. C. D.
4.2020年5月28日,十三届全国人大三次会议审议通过了《中华人民共和国民法典》,自2021年1月1日起施行,某校组织全校2000名学生参加了“学民法·树意识”普及民法知识竞赛,随机抽取200名学生成绩,统计整理后画出频率分布直方图如图所示,若成绩居于前400名的同学可以获得奖励,估计获奖同学的成绩最低分为( )
A.70分 B.80分 C.86.5分 D.87.5分
5.甲乙两名运动员在某项体能测试中的6次成绩统计如表:
甲 9 8 16 15 15 14
乙 7 8 13 15 17 22
分别表示甲乙两名运动员这项测试成绩的平均数,分别表示甲乙两名运动员这项测试成绩的标准差,则有( )A., B.,
C., D.,
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生规模群体感染的标志为“连续天,每天新增疑似病例不超过人”根据过去天甲 乙 丙 丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为,中位数为
B.乙地:总体均值为,总体方差大于
C.丙地:中位数为,众数为
D.丁地:总体均值为,总体方差为
二、多选题
7.已知数据的平均数为,标准差为,则( )
A.数据的平均数为,标准差为
B.数据的平均数为,标准差为
C.数据的平均数为,方差为
D.数据的平均数为,方差为
8.有一组样本数据,另一组样本数据,其中,c为非零常数,则( )
A.两组样本数据平均数相同 B.两组样本数据与各自平均数的“平均距离”相等
C.两组样本数据方差相同 D.两组样本数据极差相同
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.已知某高级中学高一 高二 高三三个年级的学生人数分别为880人 860人 820人,现用分层抽样方法从该校三个年级抽出128人参加社会实践活动问卷调查,则在高二年级抽出的人数为___________.
10.已知某样本数据分别为1,4,3,a,6,且样本均值,则样本方差_________.
11.某学校在校学生有2000人,为了增强学生的体质,学校举行了跑步和登山比赛,每人都参加且只参加其中一项比赛,高一、高二、高三年级参加跑步的人数分别为a,b,c,且,全校参加登山的人数占总人数的.为了了解学生对本次比赛的满意程度,按分层抽样的方法从中抽取一个容量为200的样本进行调查,则应从高三年级参加跑步的学生中抽取人数为______.
12.已知一组数据4,,,5,7的平均数为4,则这组数的方差是________.
四、解答题
13.某样本由个数组成,平均数为,方差为.这个样本可分为两层:第一层有m个数,分别为,,…,,平均数为,方差为;第二层有n个数,分别为,,…,,平均数为,方差为.
(1)证明:;
(2)证明:,;
(3)证明:.
14.随着新冠肺炎疫情的稳定,各地的经济均呈现缓慢的恢复趋势,为了更进一步做好疫情的防控工作,避免疫情的再度爆发,A地区规定居民出行或者出席公共场合均需佩戴口罩,现将A地区20000个居民一周的口罩使用个数统计如下表所示,其中每周的口罩使用个数在6以上(含6)的有14000人.
口罩使用数量
频率 0.2 m 0.3 n 0.1
(1)求m,n的值;
(2)根据表中数据,完善上面的频率分布直方图;
(3)计算A地区居民一周口罩使用个数的平均数以及方差.
15.在下列项目中选择适当的问题,对你所收集的数据确定一个标题,明确需要解决的问题,并说明数据的收集方法与数据处理 分析的方法和过程.
(1)某项体育比赛的成绩记录;
(2)天气报告——温度 雨量 湿度 暴风雨;
(3)交通运输记录——事故 运输量 车辆数 停车场的数量;
(4)商业状况——销售额 价格 银行存款 利率;
(5)校服的款式 颜色;
(6)看电视 看电影,借阅图书杂志.
16.中医药文化历史悠久.我国经历了数千年的艰难探索和发展,逐渐积淀成博大精深的中医药文化.某医药采购商计划从云南昭通购买500千克乌天麻,购买数据如下表:
乌天麻规格 (支/千克)
数量(千克) 200 100 150 50
(1)估计每千克乌天麻的平均支数(同一组中的数据用该区间的中点值作代表);
(2)已知生产商提供该产品的两种销售方案供采购商选择,
方案一:这500千克乌天麻一律售价为280元/千克.
方案二:这500千克按规格不同售出,其售价如下:
乌天麻规格 (支/千克)
售价(元/千克) 300 280 260 240
从采购商的角度考虑,应该选择哪种方案 请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
从指定位置起依次读两位数码,超出编号的数删除.
【详解】
根据题意,从随机数表第9行第5列的数1开始向右读,
依次选出的号码数是:12,34,29,56,07,52;
所以第6个个体是52.
故选:D.
2.C
【解析】
【分析】
根据茎叶图即可判断各选项的真假.
【详解】
对A ,的极差是,的极差是,两者不相等,故A选项错误;
对B ,的中位数是,的中位数是55,故的中位数较小,故B选项错误;
对C ,的众数为55,与中位数相同,故C选项正确;
对D ,的平均数是49.9,的平均数是52.9,不相等,故D选项错误.
故选:C.
3.A
【解析】
【分析】
根据已知条件可得出关于、的方程组,解出这两个量的值,即可求得结果.
【详解】
由题意有,得,
又由,得,
解得,,有.
故选:A.
4.D
【解析】
【分析】
根据频率分布直方图求出第i组的频率为,设获奖的最低分为a,由题意列方程求出即可.
【详解】
设频率分布直方图第i组的频率为,则
.
全校2000名学生中前400名的同学可以获得奖励,所以获奖同学的概率为,
故获奖的最低分落在区间.设获奖的最低分为a,则:
,
解得:.
故选:D
5.B
【解析】
【分析】
根据给定统计表计算、,再比较、大小判断作答.
【详解】
依题意,,,
,
,
所以,.
故选:B
6.D
【解析】
【分析】
利用平均数、中位数、方差的计算公式以及含义,对四个选项逐一分析判断即可.
【详解】
因为平均数和中位数不能限制某一天的病例超过人,故A不正确;
乙地:总体均值为,说明乙地过去天新增疑似病例例,
总体方差大于,有可能存在一天新增疑似病例超过人,故B不正确;
中位数和众数也不能限制某一天的病例超过人,故C不正确;
当总体平均数是,若有一个数据超过,则方差就超过,故D正确,
故选:D.
7.BC
【解析】
【分析】
根据平均数、方差、标准差的定义逐项判断可得答案.
【详解】
, ,
对于A,与不存在关系,不一定相等,故错误;
对于B,,,所以数据的标准差为,故正确;
对于C,,,故正确;
对于D,数据的平均数为,方差为
,故错误.
故选:BC.
8.BCD
【解析】
【分析】
根据题意,结合平均数、方差、极差、“平均距离”的计算公式,一一判断即可.
【详解】
对于选项A, ,,故A错;
对于选项B, ,,故B正确;
对于选项C,,,故C正确;
对于选项D,,故D正确.
故选:BCD.
9.43
【解析】
【分析】
求出抽样比可得答案.
【详解】
由题意可知,在高二年级中抽调的人数为(人).
故答案为:43.
10.##
【解析】
【分析】
先求得的值,然后求得样本方差.
【详解】
依题意,
所以.
故答案为:
11.
【解析】
【分析】
由题意求得样本中抽取的高三的人数为人进而求得样本中高三年级参加登山的人,即可求解.
【详解】
由题意,高一、高二、高三年级参加跑步的人数分别为a,b,c,且,
所以样本中抽取的高三的人数为人,
又因为全校参加登山的人数占总人数的,
所以样本中高三年级参加登山的人数为,
所以样本中高三年级参加跑步的人数为人.
故答案为:.
12.3.6
【解析】
【分析】
先根据这组数据的平均数为4,求得a,再利用方差公式求解.
【详解】
因为一组数据4,,,5,7的平均数为4,
所以,
解得,
所以这组数据为,
所以这组数据的方差为
故答案为:3.6
13.(1)证明见解析;
(2)证明见解析;
(3)证明见解析.
【解析】
【分析】
(1)利用平均数的定义及计算公式即证;
(2)利用平均数的含义及计算公式即证;
(3)利用平均数、方差的定义及计算公式即证;
(1)
根据平均数定义,,
故,
因此.
(2)
因为,,
所以.
因为,,
所以
.
(3)
方法一:由方差定义可得,由(2)可知,
所以
.
同理,于是
将代入化简得.
方法二:由题设,所以
.
同理,于是
将代入化简得.
14.(1),;
(2)频率分布直方图见解析;
(3)平均数是7,方差是.
【解析】
【分析】
(1)由每周的口罩使用个数在6以上(含6)的有14000人求出6以上(含6)的频率,从而可得值,同样由6个以下的频率求得;
(2)根据频率表作出频率分布直方图;
(3)由每组数据中点值乘以频率相加得平均值,由每组数据中点值减去平均值后平方再乘以频率相加得方差.
(1)
由已知,;
(2)
频率分布直方图如下:
(3)
由频率分布直方图得
一周内使用口罩的平均数为
,
方差为.
15.(1)
(2)
(3)
(4)
(5)
(6)
【解析】
略
16.(1)16支
(2)选择方案二,理由见解析
【解析】
【分析】
(1)根据频率分布表,利用平均数公式求解;
(2)根据频率分布表,利用平均数公式求得方案二的产品的平均售价,再比较下结论.
(1)
解:,
所以该采购商购买的乌天麻每千克的平均支数为16支.
(2)
由题意知:方案二的产品的平均售价为:
(元/千克).
因为278<280,所以从采购商的角度考虑,选择方案二.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
