2021—2022学年人教版八年级数学下册17.2勾股定理的逆定理课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册17.2勾股定理的逆定理课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 18:37:14 | ||
图片预览



文档简介
2021——2022学年度人教版八年级数学下册 第十七章勾股定理
17.2 勾股定理的逆定理 课后练习题
一、选择题
1.在下列四组线段中,能组成直角三角形的是( )
A.a=32,b=42,c=52 B.a=4,b=5,c=6
C.a=9,b=12,c=15 D.a:b:c=1:1:2
2.如果三角形的三边分别为,,2,那么这个三角形的最大角的度数为( )
A.30° B.45° C.60° D.90°
3.下列叙述中,正确的是
A.直角三角形中,两条边的平方和等于第三边的平方
B.如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形是直角三角形
C.中,∠A,∠B,∠C的对边分别为a,b,c,若,则∠A=90
D.中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90 ,则
4.已知.指出以a,b,c为边长的直角三角形中哪一条边所对的角是直角( ).
A.a B.b C.c D.无法确定
5.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
6.如图,△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),则△ABC与△DEF的面积比是( )
A.1:2 B.2:5 C.: D.1:3
7.如图,在四边形中,,,,,.则的大小为( )
A. B. C. D.
8.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
9.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,则该沙田的面积为( )(“里”是我国市制长度单位,里米)
A.平方千米 B.平方千米 C.平方千米 D.平方千米
10.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
二、填空题
11.△ABC的三条边长、、满足,,则△ABC____直角三角形(填“是”或“不是”)
12.如图,正方形网格中,每一小格的边长为1.网格内有△PAB,则∠PAB+∠PBA的度数是______.
13.已知三角形的三边分别是6,8,10,则最长边上的高等于______.
14.如图,在四边形中,为的中点,于点,,,,,则四边形的面积为_____.
15.如图,快艇计划从A地到距离A地10海里的C地,先沿北偏东72°方向行驶8海里到达B地,再从B地行驶6海里到达C地,此时快艇位于B地的方向是___.
三、解答题
16.已知△ABC中,AB=1,AC=,BC=,求△ABC中的最大内角的度数.
17.如图,在△ABC中,CD⊥AB,垂足为D.AD=1,BD=4,CD=2.求证:∠ACB=90°.
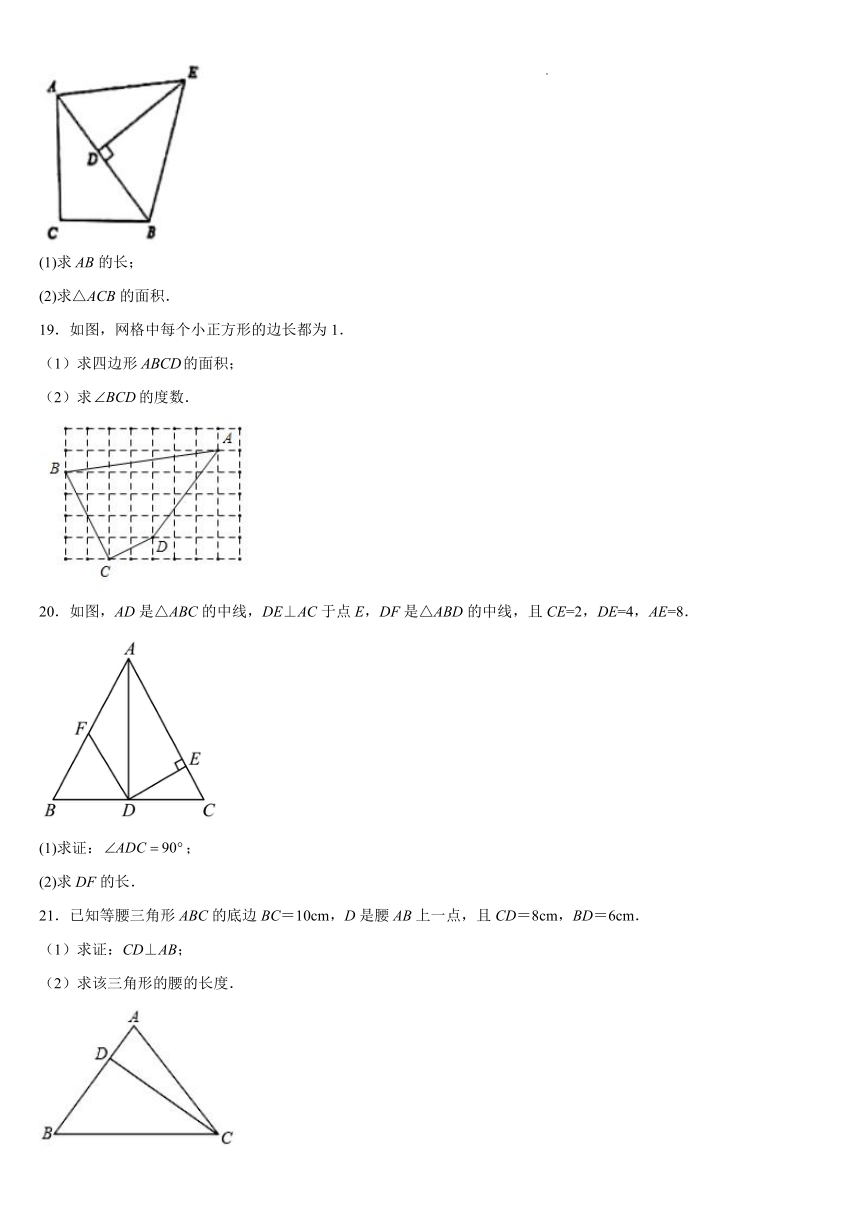
18.如图,在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35.
(1)求AB的长;
(2)求△ACB的面积.
19.如图,网格中每个小正方形的边长都为1.
(1)求四边形的面积;
(2)求的度数.
20.如图,AD是△ABC的中线,DE⊥AC于点E,DF是△ABD的中线,且CE=2,DE=4,AE=8.
(1)求证:;
(2)求DF的长.
21.已知等腰三角形ABC的底边BC=10cm,D是腰AB上一点,且CD=8cm,BD=6cm.
(1)求证:CD⊥AB;
(2)求该三角形的腰的长度.
22.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
23.已知:在四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,CD=13.
(1)求AC的长.
(2)ACD是直角三角形吗?如果是,请说明理由.
(3)求这块空地的面积.
【参考答案】
1.C 2.D 3.B 4.C 5.D 6.B 7.D 8.D 9.A 10.D
11.不是
12.45°
13.4.8
14.
15.北偏西18°
16.在△ABC中,
,,,
,
∴△ABC为直角三角形,且最大角为边所对的直角,
则△ABC中的最大内角的度数为90°.
17.证明:∵CD是△ABC的高,
∴∠ADC=∠BDC=90°.
∵AD=1,BD=4,CD=2,
∴AC2=AD2+CD2=12+22=5,BC2=BD2+CD2=42+22=20,AB2=(1+4)2=25.
∴AC2+BC2=AB2.
∴△ABC是直角三角形,
∴∠ACB=90°.
18.(1)解:∵△ABE的面积为35,DE=7,DE⊥AB,
∴AB×7=35,
解得:AB=10;
(2)解:在△ABC中,AB2=102=100,AC2+BC2=62+82=100,
则AB2=AC2+BC2,
∴∠C=90°,
∴S△ABC=AC BC=×6×8=24,
答:△ACB的面积24.
19.解:(1)
(2)连接,
∵,,
∴
∴是直角三角形,∴
20.(1)证明:∵DE⊥AC于点E,
∴∠AED=∠CED=90°,
在Rt△ADE中,∠AED=90°,
∴AD2=AE2+DE2=82+42=80,
同理:CD2=20,
∴AD2+CD2=80+20=100,
∵AC=AE+CE=8+2=10,
∴AC2=100,
∴AD2+CD2=AC2,
∴△ADC是直角三角形,
∴∠ADC=90°;
(2)解:∵AD是△ABC的中线,∠ADC=90°,
∴AD垂直平分BC,
∴AB=AC=10,
在Rt△ADB中,∠ADB=90°,
∵点F是边AB的中点,
∴DF=AB=5.
∴DF的长为5.
21.解:证明:(1)设AB=AC=a cm,
∵BC=10cm,CD=8cm,BD=6cm,
∴BD2+CD2=BC2,
∴∠BDC=90°,
即∠ADC=90°,
∴CD⊥AB;
(2)∵∠ADC=90°,
在Rt△ADC中,由勾股定理得:AC2=AD2+CD2,
即a2=(a-6)2+82,
解得:a=,
即AB=cm.
22.(1)解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
23.解:(1)∵∠ACB=90°,AB=15,BC=9,
∴AC==12;
(2)是,理由是:
∵AC=12,AD=5,CD=13,
满足,即,
∴△ACD是直角三角形;
(3)空地的面积为:
==84.
17.2 勾股定理的逆定理 课后练习题
一、选择题
1.在下列四组线段中,能组成直角三角形的是( )
A.a=32,b=42,c=52 B.a=4,b=5,c=6
C.a=9,b=12,c=15 D.a:b:c=1:1:2
2.如果三角形的三边分别为,,2,那么这个三角形的最大角的度数为( )
A.30° B.45° C.60° D.90°
3.下列叙述中,正确的是
A.直角三角形中,两条边的平方和等于第三边的平方
B.如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形是直角三角形
C.中,∠A,∠B,∠C的对边分别为a,b,c,若,则∠A=90
D.中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90 ,则
4.已知.指出以a,b,c为边长的直角三角形中哪一条边所对的角是直角( ).
A.a B.b C.c D.无法确定
5.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
6.如图,△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),则△ABC与△DEF的面积比是( )
A.1:2 B.2:5 C.: D.1:3
7.如图,在四边形中,,,,,.则的大小为( )
A. B. C. D.
8.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
9.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,则该沙田的面积为( )(“里”是我国市制长度单位,里米)
A.平方千米 B.平方千米 C.平方千米 D.平方千米
10.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
二、填空题
11.△ABC的三条边长、、满足,,则△ABC____直角三角形(填“是”或“不是”)
12.如图,正方形网格中,每一小格的边长为1.网格内有△PAB,则∠PAB+∠PBA的度数是______.
13.已知三角形的三边分别是6,8,10,则最长边上的高等于______.
14.如图,在四边形中,为的中点,于点,,,,,则四边形的面积为_____.
15.如图,快艇计划从A地到距离A地10海里的C地,先沿北偏东72°方向行驶8海里到达B地,再从B地行驶6海里到达C地,此时快艇位于B地的方向是___.
三、解答题
16.已知△ABC中,AB=1,AC=,BC=,求△ABC中的最大内角的度数.
17.如图,在△ABC中,CD⊥AB,垂足为D.AD=1,BD=4,CD=2.求证:∠ACB=90°.
18.如图,在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35.
(1)求AB的长;
(2)求△ACB的面积.
19.如图,网格中每个小正方形的边长都为1.
(1)求四边形的面积;
(2)求的度数.
20.如图,AD是△ABC的中线,DE⊥AC于点E,DF是△ABD的中线,且CE=2,DE=4,AE=8.
(1)求证:;
(2)求DF的长.
21.已知等腰三角形ABC的底边BC=10cm,D是腰AB上一点,且CD=8cm,BD=6cm.
(1)求证:CD⊥AB;
(2)求该三角形的腰的长度.
22.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
23.已知:在四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,CD=13.
(1)求AC的长.
(2)ACD是直角三角形吗?如果是,请说明理由.
(3)求这块空地的面积.
【参考答案】
1.C 2.D 3.B 4.C 5.D 6.B 7.D 8.D 9.A 10.D
11.不是
12.45°
13.4.8
14.
15.北偏西18°
16.在△ABC中,
,,,
,
∴△ABC为直角三角形,且最大角为边所对的直角,
则△ABC中的最大内角的度数为90°.
17.证明:∵CD是△ABC的高,
∴∠ADC=∠BDC=90°.
∵AD=1,BD=4,CD=2,
∴AC2=AD2+CD2=12+22=5,BC2=BD2+CD2=42+22=20,AB2=(1+4)2=25.
∴AC2+BC2=AB2.
∴△ABC是直角三角形,
∴∠ACB=90°.
18.(1)解:∵△ABE的面积为35,DE=7,DE⊥AB,
∴AB×7=35,
解得:AB=10;
(2)解:在△ABC中,AB2=102=100,AC2+BC2=62+82=100,
则AB2=AC2+BC2,
∴∠C=90°,
∴S△ABC=AC BC=×6×8=24,
答:△ACB的面积24.
19.解:(1)
(2)连接,
∵,,
∴
∴是直角三角形,∴
20.(1)证明:∵DE⊥AC于点E,
∴∠AED=∠CED=90°,
在Rt△ADE中,∠AED=90°,
∴AD2=AE2+DE2=82+42=80,
同理:CD2=20,
∴AD2+CD2=80+20=100,
∵AC=AE+CE=8+2=10,
∴AC2=100,
∴AD2+CD2=AC2,
∴△ADC是直角三角形,
∴∠ADC=90°;
(2)解:∵AD是△ABC的中线,∠ADC=90°,
∴AD垂直平分BC,
∴AB=AC=10,
在Rt△ADB中,∠ADB=90°,
∵点F是边AB的中点,
∴DF=AB=5.
∴DF的长为5.
21.解:证明:(1)设AB=AC=a cm,
∵BC=10cm,CD=8cm,BD=6cm,
∴BD2+CD2=BC2,
∴∠BDC=90°,
即∠ADC=90°,
∴CD⊥AB;
(2)∵∠ADC=90°,
在Rt△ADC中,由勾股定理得:AC2=AD2+CD2,
即a2=(a-6)2+82,
解得:a=,
即AB=cm.
22.(1)解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
23.解:(1)∵∠ACB=90°,AB=15,BC=9,
∴AC==12;
(2)是,理由是:
∵AC=12,AD=5,CD=13,
满足,即,
∴△ACD是直角三角形;
(3)空地的面积为:
==84.
