2021-2022学年鲁教版六年级数学下册第一次阶段测试综合练习题(Word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版六年级数学下册第一次阶段测试综合练习题(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 18:41:15 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学下册第一次阶段测试综合练习题(附答案)
一、选择(共36分)
1.两点之间的所有连线中,最短的是( )
A.直线 B.射线 C.线段 D.圆弧
2.过平面内已知点A作直线,可作直线的条数为( )
A.0条 B.1条 C.2条 D.无数条
3.如图,下面四种表示角的方法,其中正确的是( )
A.∠A B.∠B C.∠C D.∠D
4.计算x2 x3的结果为( )
A.2x2 B.x5 C.2x3 D.x6
5.计算(﹣a3)2的结果是( )
A.﹣a5 B.a5 C.﹣a6 D.a6
6.2﹣3可以表示为( )
A.22÷25 B.25÷22 C.22×25 D.(﹣2)×(﹣2)×(﹣2)
7.0.00023用科学记数法表示为( )
A.0.23×10﹣3 B.2.3×10﹣4 C.23×10﹣5 D.2.3×104
8.如果a2m﹣1 am+2=a7,则m的值是( )
A.2 B.3 C.4 D.5
9.若x+y=3且xy=1,则代数式(1+x)(1+y)的值等于( )
A.5 B.﹣5 C.3 D.﹣3
10.计算(﹣a﹣b)2等于( )
A.a2﹣2ab+b2 B.a2+2ab+b2 C.a2+b2 D.a2﹣b2
11.如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,则∠CBD等于多少度( )
A.70° B.80° C.90° D.70°
12.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
根据“杨辉三角”请计算(a+b)6的展开式中从左起第四项的系数为( )
A.10 B.15 C.20 D.25
二、填空(24分)
13.计算的结果是 .
14.已知a+b=7,ab=1,则a2+b2= .
15.若(x+3)(x﹣5)=x2+mx﹣15,则m= .
16.如图,延长线段AB到点C,使BC=2AB,取AC的中点D,且BD=2cm,则AC的长为 cm.
17.已知a=212,b=38,c=54,则a,b,c的大小关系是 .
18.将一副直角三角尺如图放置,若∠BOC=160°,则∠AOD等于 .
三、解答(60分)
19.计算:
(1)a (﹣a3)2;
(2)20212﹣2019×2023;
(3)(2x﹣y+3)2;
(4)(m﹣2n+1)(m+2n+1).
20.已知am=2,an=5,求a3m﹣2n的值.
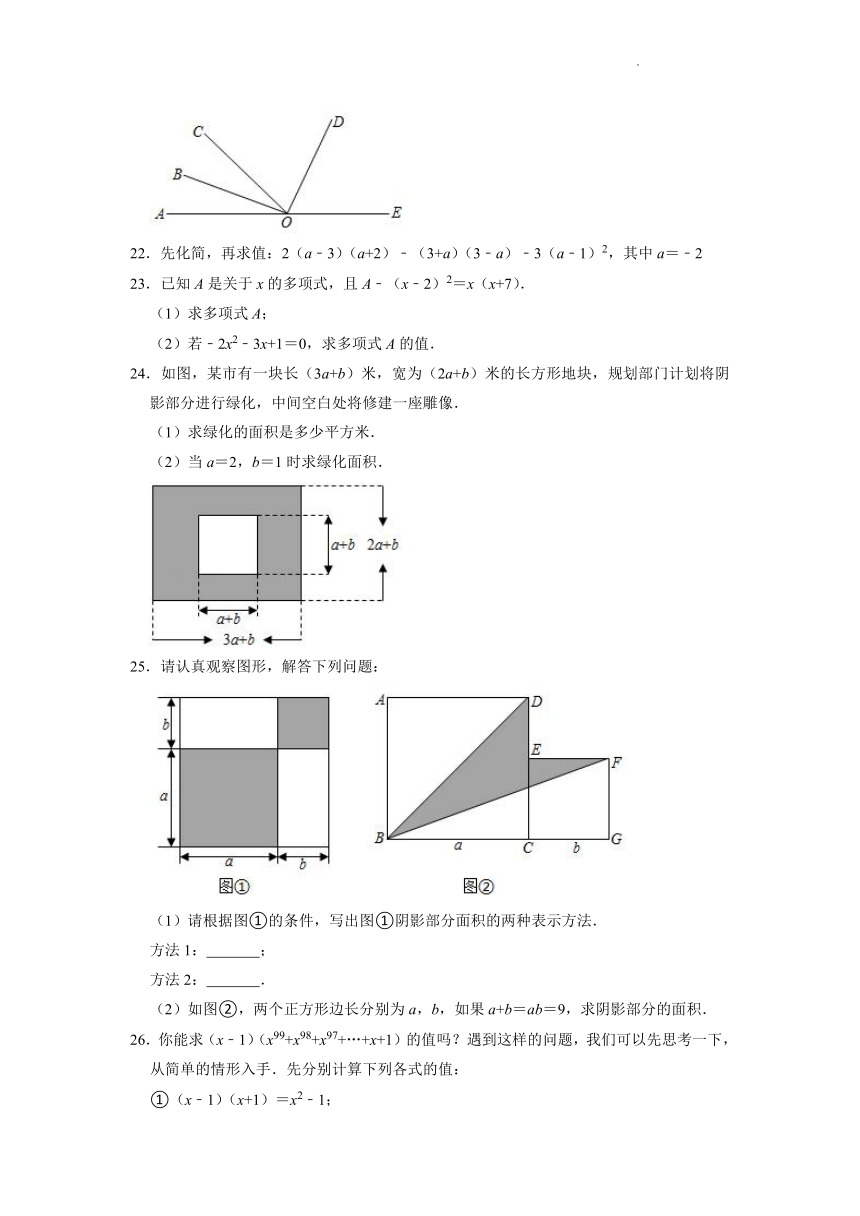
21.如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=∠AOB.
(1)求∠EOC的度数;
(2)如果OD平分∠EOC,求∠BOD的度数.
22.先化简,再求值:2(a﹣3)(a+2)﹣(3+a)(3﹣a)﹣3(a﹣1)2,其中a=﹣2
23.已知A是关于x的多项式,且A﹣(x﹣2)2=x(x+7).
(1)求多项式A;
(2)若﹣2x2﹣3x+1=0,求多项式A的值.
24.如图,某市有一块长(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间空白处将修建一座雕像.
(1)求绿化的面积是多少平方米.
(2)当a=2,b=1时求绿化面积.
25.请认真观察图形,解答下列问题:
(1)请根据图①的条件,写出图①阴影部分面积的两种表示方法.
方法1: ;
方法2: .
(2)如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
26.你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1;
(2)若x3+x2+x+1=0,求x2020.
参考答案
一、选择(共36分)
1.解:在两点之间的所有连线中,线段最短.
故选:C.
2.解:过平面内已知点A作直线,可作直线的条数为无数条,
故选:D.
3.解:图中的角有∠A、∠ABC、∠BCD、∠ADC,
即表示方法正确的有∠A,
故选:A.
4.解:原式=x2+3
=x5.
故选:B.
5.解:(﹣a3)2=a6,
故选:D.
6.解:A、22÷25=22﹣5=2﹣3,故正确;
B、25÷22=23,故错误;
C、22×25=27,故错误;
D、(﹣2)×(﹣2)×(﹣2)=(﹣2)3,故错误;
故选:A.
7.解:0.00023=2.3×10﹣4.
故选:B.
8.解:根据题意得:2m﹣1+(m+2)=7,
解得:m=2.
故选:A.
9.解:当x+y=3、xy=1时,
原式=1+y+x+xy
=1+3+1
=5,
故选:A.
10.解:原式=[﹣(a+b)]2
=(a+b)2
=a2+2ab+b2,
故选:B.
11.解:由翻折的性质得,∠ABC=∠A′BC,
∵BD平分∠A′BE,
∴∠A′BD=∠EBD,
∵∠ABC+∠A′BC+∠A′BD+∠EBD=180°,
∴∠A′BC+∠A′BD=90°,
即∠CBD=90°.
故选:C.
12.解:找规律发现(a+b)4的第四项系数为4=3+1;
(a+b)5的第四项系数为10=6+4;
∴(a+b)6的第四项系数为20=10+10.
故选:C.
二、填空(24分)
13.解:()﹣1==2.
故答案为:2.
14.解:∵a+b=7,ab=1,
∴a2+b2=(a+b)2﹣2ab
=72﹣2×1
=49﹣2
=47.
故答案为:47.
15.解:∵(x+3)(x﹣5)=x2﹣2x﹣15,
∴m=﹣2,
∴m=﹣2.
故答案为:﹣2.
16.解:AB=xcm,则BC=2xcm,
∵AC=AB+BC,
∴AC=3x,
∵点D是AC的中点,
∴AD=AC=1.5x,
∵BD=AD﹣AB,
∴1.5x﹣x=2,
解得:x=4,
∴AC=3x=3×4=12(cm),
故答案为:12.
17.解:∵a=212=(23)4=84,b=38=(32)4=94,c=54,
而54<84<94,
∴c<a<b,
故答案为:c<a<b.
18.解:∵∠COB=∠COD+∠AOB﹣∠AOD,
∴90°+90°﹣∠AOD=160°,
∴∠AOD=20°.
故答案为:20°.
三、解答(60分)
19.解:(1)a (﹣a3)2
=a a6
=a7;
(2)20212﹣2019×2023
=20212﹣(2021﹣2)×(2021+2)
=20212﹣20212+4
=4;
(3)(2x﹣y+3)2
=[(2x﹣y)+3]2
=(2x﹣y)2+6(2x﹣y)+9
=4x2﹣4xy+y2+12x﹣6y+9;
(4)(m﹣2n+1)(m+2n+1)
=[(m+1)﹣2n][(m+1)+2n]
=(m+1)2﹣4n2
=m2+2m+1﹣4n2.
20.解:∵am=2,an=5,
∴a3m﹣2n=a3m÷a2n=(am)3÷(an)2=23÷52=.
21.解:(1)∵∠AOB=30°,∠BOC=∠AOB,
∴∠AOC=2∠AOB=60°,
∴∠EOC=120°.
(2)∵∠EOC=120°,OD平分∠EOC,
∴∠COD=∠EOC=60°,
∴∠BOD=∠COB+∠COD=30°+60°=90°.
22.解:2(a﹣3)(a+2)﹣(3+a)(3﹣a)﹣3(a﹣1)2
=2a2+4a﹣6a﹣12﹣9+a2﹣3a2+6a﹣3
=4a﹣24,
当a=﹣2时,原式=﹣8﹣24=﹣32.
23.解:(1)∵A﹣(x﹣2)2=x(x+7),
∴A=(x﹣2)2+x(x+7)
=x2﹣4x+4+x2+7x
=2x2+3x+4;
(2)∵﹣2x2﹣3x+1=0,
∴2x2+3x﹣1=0,
∴2x2+3x=1,
∴A=1+4=5.
24.解:(1)S绿化面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab;
答:绿化的面积是(5a2+3ab)平方米;
(2)当a=2,b=1时,绿化面积=5×22+3×2×1
=20+6
=26.
答:当a=2,b=1时,绿化面积为26平方米.
25.解:(1)方法1:阴影部分的面积=2个小正方形面积的和,即:a2+b2;
方法2:阴影部分的面积=大正方形的面积﹣2个长方形的面积,即:(a+b)2﹣2ab;
故答案为:a2+b2;(a+b)2﹣2ab;
(2)阴影部分的面积=a2+b2﹣a2﹣(a+b)b
=a2+b2﹣a2﹣ab﹣b2
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab]
当a+b=ab=9时,
原式=×(92﹣3×9)=27,
所以,阴影部分的面积为27.
26.解:由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)=x100﹣1;
故答案为:x100﹣1;
(1)原式=﹣(﹣2﹣1)×[(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1]
=﹣[(﹣2)51﹣1]
=;
(2)∵x≠1,
∴已知等式变形得:(x﹣1)(x3+x2+x+1)=0,
∴x﹣1=0(x3+x2+x+1≠0),
解得:x=1,
则原式=1.
一、选择(共36分)
1.两点之间的所有连线中,最短的是( )
A.直线 B.射线 C.线段 D.圆弧
2.过平面内已知点A作直线,可作直线的条数为( )
A.0条 B.1条 C.2条 D.无数条
3.如图,下面四种表示角的方法,其中正确的是( )
A.∠A B.∠B C.∠C D.∠D
4.计算x2 x3的结果为( )
A.2x2 B.x5 C.2x3 D.x6
5.计算(﹣a3)2的结果是( )
A.﹣a5 B.a5 C.﹣a6 D.a6
6.2﹣3可以表示为( )
A.22÷25 B.25÷22 C.22×25 D.(﹣2)×(﹣2)×(﹣2)
7.0.00023用科学记数法表示为( )
A.0.23×10﹣3 B.2.3×10﹣4 C.23×10﹣5 D.2.3×104
8.如果a2m﹣1 am+2=a7,则m的值是( )
A.2 B.3 C.4 D.5
9.若x+y=3且xy=1,则代数式(1+x)(1+y)的值等于( )
A.5 B.﹣5 C.3 D.﹣3
10.计算(﹣a﹣b)2等于( )
A.a2﹣2ab+b2 B.a2+2ab+b2 C.a2+b2 D.a2﹣b2
11.如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,则∠CBD等于多少度( )
A.70° B.80° C.90° D.70°
12.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
根据“杨辉三角”请计算(a+b)6的展开式中从左起第四项的系数为( )
A.10 B.15 C.20 D.25
二、填空(24分)
13.计算的结果是 .
14.已知a+b=7,ab=1,则a2+b2= .
15.若(x+3)(x﹣5)=x2+mx﹣15,则m= .
16.如图,延长线段AB到点C,使BC=2AB,取AC的中点D,且BD=2cm,则AC的长为 cm.
17.已知a=212,b=38,c=54,则a,b,c的大小关系是 .
18.将一副直角三角尺如图放置,若∠BOC=160°,则∠AOD等于 .
三、解答(60分)
19.计算:
(1)a (﹣a3)2;
(2)20212﹣2019×2023;
(3)(2x﹣y+3)2;
(4)(m﹣2n+1)(m+2n+1).
20.已知am=2,an=5,求a3m﹣2n的值.
21.如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=∠AOB.
(1)求∠EOC的度数;
(2)如果OD平分∠EOC,求∠BOD的度数.
22.先化简,再求值:2(a﹣3)(a+2)﹣(3+a)(3﹣a)﹣3(a﹣1)2,其中a=﹣2
23.已知A是关于x的多项式,且A﹣(x﹣2)2=x(x+7).
(1)求多项式A;
(2)若﹣2x2﹣3x+1=0,求多项式A的值.
24.如图,某市有一块长(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间空白处将修建一座雕像.
(1)求绿化的面积是多少平方米.
(2)当a=2,b=1时求绿化面积.
25.请认真观察图形,解答下列问题:
(1)请根据图①的条件,写出图①阴影部分面积的两种表示方法.
方法1: ;
方法2: .
(2)如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
26.你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1;
(2)若x3+x2+x+1=0,求x2020.
参考答案
一、选择(共36分)
1.解:在两点之间的所有连线中,线段最短.
故选:C.
2.解:过平面内已知点A作直线,可作直线的条数为无数条,
故选:D.
3.解:图中的角有∠A、∠ABC、∠BCD、∠ADC,
即表示方法正确的有∠A,
故选:A.
4.解:原式=x2+3
=x5.
故选:B.
5.解:(﹣a3)2=a6,
故选:D.
6.解:A、22÷25=22﹣5=2﹣3,故正确;
B、25÷22=23,故错误;
C、22×25=27,故错误;
D、(﹣2)×(﹣2)×(﹣2)=(﹣2)3,故错误;
故选:A.
7.解:0.00023=2.3×10﹣4.
故选:B.
8.解:根据题意得:2m﹣1+(m+2)=7,
解得:m=2.
故选:A.
9.解:当x+y=3、xy=1时,
原式=1+y+x+xy
=1+3+1
=5,
故选:A.
10.解:原式=[﹣(a+b)]2
=(a+b)2
=a2+2ab+b2,
故选:B.
11.解:由翻折的性质得,∠ABC=∠A′BC,
∵BD平分∠A′BE,
∴∠A′BD=∠EBD,
∵∠ABC+∠A′BC+∠A′BD+∠EBD=180°,
∴∠A′BC+∠A′BD=90°,
即∠CBD=90°.
故选:C.
12.解:找规律发现(a+b)4的第四项系数为4=3+1;
(a+b)5的第四项系数为10=6+4;
∴(a+b)6的第四项系数为20=10+10.
故选:C.
二、填空(24分)
13.解:()﹣1==2.
故答案为:2.
14.解:∵a+b=7,ab=1,
∴a2+b2=(a+b)2﹣2ab
=72﹣2×1
=49﹣2
=47.
故答案为:47.
15.解:∵(x+3)(x﹣5)=x2﹣2x﹣15,
∴m=﹣2,
∴m=﹣2.
故答案为:﹣2.
16.解:AB=xcm,则BC=2xcm,
∵AC=AB+BC,
∴AC=3x,
∵点D是AC的中点,
∴AD=AC=1.5x,
∵BD=AD﹣AB,
∴1.5x﹣x=2,
解得:x=4,
∴AC=3x=3×4=12(cm),
故答案为:12.
17.解:∵a=212=(23)4=84,b=38=(32)4=94,c=54,
而54<84<94,
∴c<a<b,
故答案为:c<a<b.
18.解:∵∠COB=∠COD+∠AOB﹣∠AOD,
∴90°+90°﹣∠AOD=160°,
∴∠AOD=20°.
故答案为:20°.
三、解答(60分)
19.解:(1)a (﹣a3)2
=a a6
=a7;
(2)20212﹣2019×2023
=20212﹣(2021﹣2)×(2021+2)
=20212﹣20212+4
=4;
(3)(2x﹣y+3)2
=[(2x﹣y)+3]2
=(2x﹣y)2+6(2x﹣y)+9
=4x2﹣4xy+y2+12x﹣6y+9;
(4)(m﹣2n+1)(m+2n+1)
=[(m+1)﹣2n][(m+1)+2n]
=(m+1)2﹣4n2
=m2+2m+1﹣4n2.
20.解:∵am=2,an=5,
∴a3m﹣2n=a3m÷a2n=(am)3÷(an)2=23÷52=.
21.解:(1)∵∠AOB=30°,∠BOC=∠AOB,
∴∠AOC=2∠AOB=60°,
∴∠EOC=120°.
(2)∵∠EOC=120°,OD平分∠EOC,
∴∠COD=∠EOC=60°,
∴∠BOD=∠COB+∠COD=30°+60°=90°.
22.解:2(a﹣3)(a+2)﹣(3+a)(3﹣a)﹣3(a﹣1)2
=2a2+4a﹣6a﹣12﹣9+a2﹣3a2+6a﹣3
=4a﹣24,
当a=﹣2时,原式=﹣8﹣24=﹣32.
23.解:(1)∵A﹣(x﹣2)2=x(x+7),
∴A=(x﹣2)2+x(x+7)
=x2﹣4x+4+x2+7x
=2x2+3x+4;
(2)∵﹣2x2﹣3x+1=0,
∴2x2+3x﹣1=0,
∴2x2+3x=1,
∴A=1+4=5.
24.解:(1)S绿化面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab;
答:绿化的面积是(5a2+3ab)平方米;
(2)当a=2,b=1时,绿化面积=5×22+3×2×1
=20+6
=26.
答:当a=2,b=1时,绿化面积为26平方米.
25.解:(1)方法1:阴影部分的面积=2个小正方形面积的和,即:a2+b2;
方法2:阴影部分的面积=大正方形的面积﹣2个长方形的面积,即:(a+b)2﹣2ab;
故答案为:a2+b2;(a+b)2﹣2ab;
(2)阴影部分的面积=a2+b2﹣a2﹣(a+b)b
=a2+b2﹣a2﹣ab﹣b2
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab]
当a+b=ab=9时,
原式=×(92﹣3×9)=27,
所以,阴影部分的面积为27.
26.解:由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)=x100﹣1;
故答案为:x100﹣1;
(1)原式=﹣(﹣2﹣1)×[(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1]
=﹣[(﹣2)51﹣1]
=;
(2)∵x≠1,
∴已知等式变形得:(x﹣1)(x3+x2+x+1)=0,
∴x﹣1=0(x3+x2+x+1≠0),
解得:x=1,
则原式=1.
同课章节目录
