2021-2022学年鲁教版八年级数学下册第6章特殊平行四边形单元测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册第6章特殊平行四边形单元测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 376.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学下册《第6章特殊平行四边形》单元综合测试题(附答案)
一.选择题(共10小题,满分40分)
1.已知菱形的两条对角线的长分别为6cm和8cm,则这个菱形的面积是( )
A.20cm2 B.24cm2 C.48cm2 D.100cm2
2.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ACDB是菱形的依据是( )
A.对角线互相垂直的平行四边形是菱形 B.对角线平分一组对角的四边形是菱形
C.一组邻边相等的四边形是菱形 D.四条边相等的四边形是菱形
3.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形 B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是正方形
4.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
5.如图,点E、F在矩形ABCD的对角线BD所在的直线上,BE=DF,则四边形AECF是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
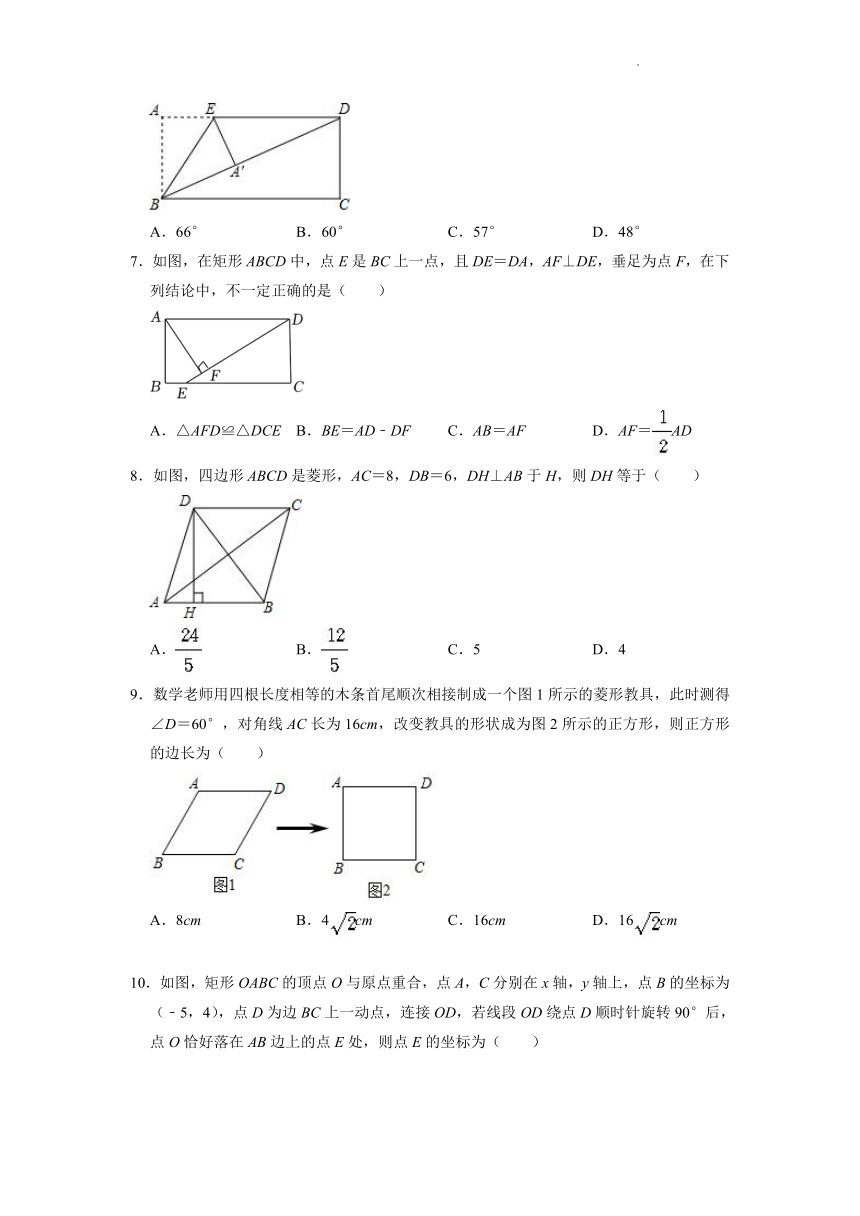
6.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
7.如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE B.BE=AD﹣DF C.AB=AF D.AF=AD
8.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
9.数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得∠D=60°,对角线AC长为16cm,改变教具的形状成为图2所示的正方形,则正方形的边长为( )
A.8cm B.4cm C.16cm D.16cm
10.如图,矩形OABC的顶点O与原点重合,点A,C分别在x轴,y轴上,点B的坐标为(﹣5,4),点D为边BC上一动点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )
A.(﹣5,3) B.(﹣5,4) C.(﹣5,) D.(﹣5,2)
二.填空题(共8小题,满分40分)
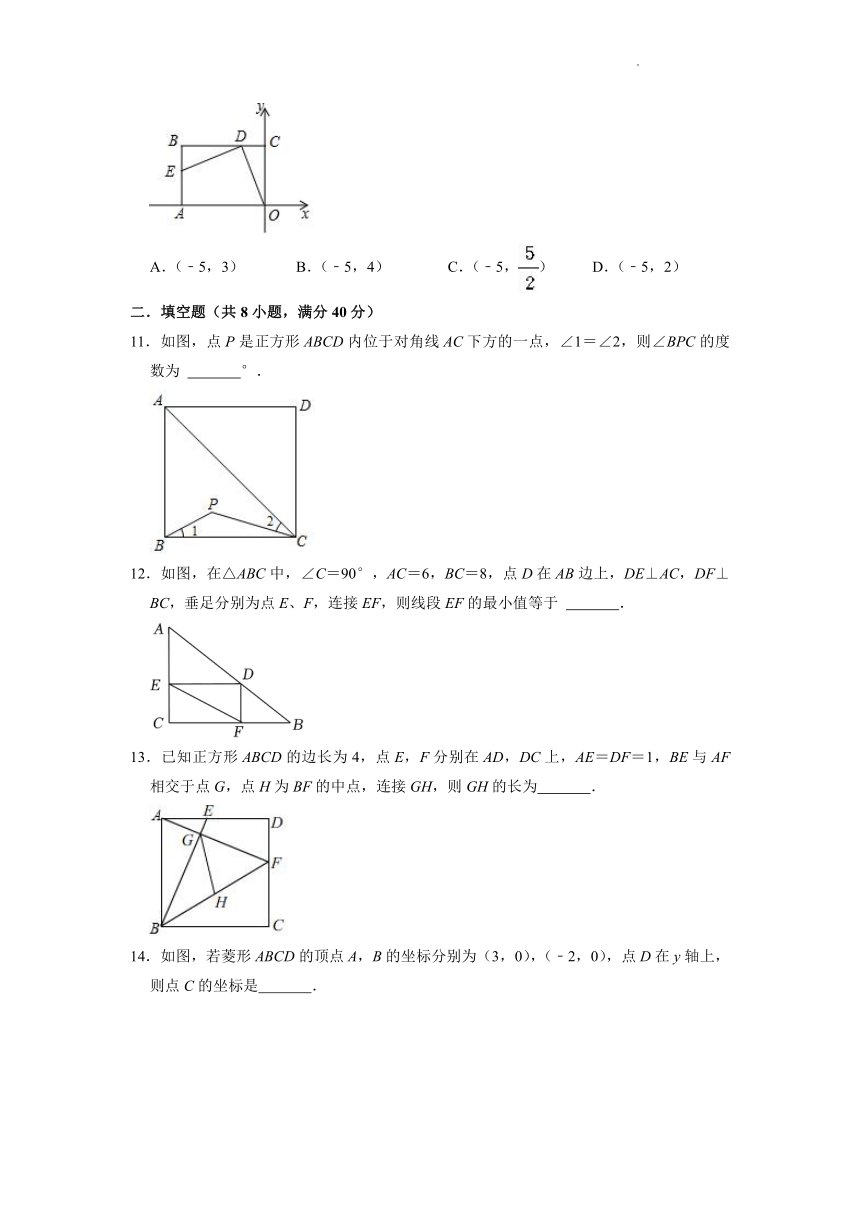
11.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
12.如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于 .
13.已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
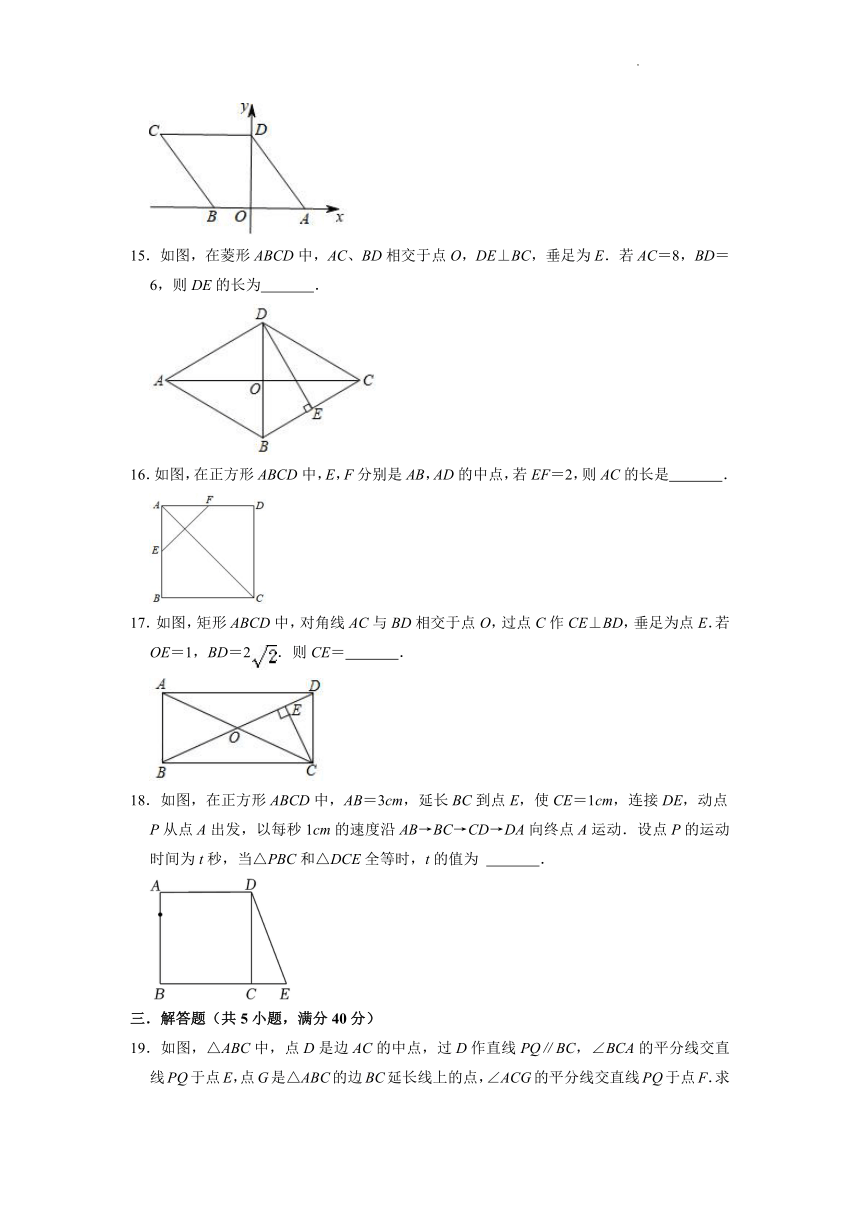
14.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是 .
15.如图,在菱形ABCD中,AC、BD相交于点O,DE⊥BC,垂足为E.若AC=8,BD=6,则DE的长为 .
16.如图,在正方形ABCD中,E,F分别是AB,AD的中点,若EF=2,则AC的长是 .
17.如图,矩形ABCD中,对角线AC与BD相交于点O,过点C作CE⊥BD,垂足为点E.若OE=1,BD=2.则CE= .
18.如图,在正方形ABCD中,AB=3cm,延长BC到点E,使CE=1cm,连接DE,动点P从点A出发,以每秒1cm的速度沿AB→BC→CD→DA向终点A运动.设点P的运动时间为t秒,当△PBC和△DCE全等时,t的值为 .
三.解答题(共5小题,满分40分)
19.如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.
20.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若∠C=90°,BC=16,CD=8,求菱形BNDM的周长.
21.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
22.如图,在 ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=2,BF=2,CE=1,求 ABCD的面积.
23.如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵菱形的两条对角线的长分别为6cm和8cm,
∴这个菱形的面积=×6×8=24(cm2),
故选:B.
2.解:由作图得:BA=BD,CA=CD,
∵AB=AC,
∴AB=AC=BD=CD,
∴四边形ACDB是菱形,
故选:D.
3.解:A、对角线互相平分的四边形是平行四边形,对角线相等的四边形也可能是等腰梯形等四边形,故A不符合题意;
B、对角线互相平分的四边形是平行四边形,若对角线再相等,则四边形是矩形,故B符合题意;
C、对角线互相垂直的四边形不能判定是平行四边形,也就不能判定是菱形,故C不符合题意;
D、对角线互相垂直平分的四边形是菱形,不能判断它的内角有直角,故D不符合题意;
故选:B.
4.解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
故选:B.
5.解:A.∵四边形ABCD是矩形,
∴AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形,
故本选项符合题意;
B.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是矩形,
故本选项不符合题意;
C.∵四边形ABCD是矩形,
∴不能证明AC⊥BD,
∴不能证明AC⊥EF,
故本选项不符合题意;
D.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是正方形,
故本选项不符合题意;
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
7.解:A、由矩形ABCD,AF⊥DE可得∠C=∠AFD=90°,AD∥BC,
∴∠ADF=∠DEC.
又∵DE=AD,
∴△AFD≌△DCE(AAS),故A正确;
B、由△AFD≌△DCE,可得CE=DF,
由矩形ABCD,可得BC=AD,
又∵BE=BC﹣EC,
∴BE=AD﹣DF,故B正确;
C、由△AFD≌△DCE,可得AF=CD,
由矩形ABCD,可得AB=CD,
∴AB=AF,故C正确;
D、∵∠ADF不一定等于30°,
∴直角三角形ADF中,AF不一定等于AD的一半,故D错误;
故选:D.
8.解:设AC交BD于O,
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB==5,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
9.解:如图1,图2中,连接AC.
图1中,∵四边形ABCD是菱形,
∴AD=DC,
∵∠D=60°,
∴△ADC是等边三角形,
∴AD=DC=AC=16cm,
∴正方形ABCD的边长为16cm,
故选:C.
10.解:由题可得,AO=BC=5,AB=CO=4,
由旋转可得,DE=OD,∠EDO=90°,
又∵∠B=∠OCD=90°,
∴∠EDB+∠CDO=90°=∠COD+∠CDO,
∴∠EDB=∠DOC,
∴△DBE≌△OCD(AAS),
∴BD=OC=4,
设AE=x,则BE=4﹣x=CD,
∵BD+CD=5,
∴4+4﹣x=5,
解得x=3,
∴AE=3,
∴E(﹣5,3),
故选:A.
二.填空题(共8小题,满分40分)
11.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
12.解:如图,连接CD.
∵∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
∵S△ABC=BC AC=AB CD,
∴×8×6=×10×CD,
解得CD=4.8,
∴EF=4.8.
故答案为:4.8.
13.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=4、CF=CD﹣DF=4﹣1=3,
∴BF==5,
∴GH=BF=,
故答案为:.
14.解:∵菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,
∴AB=5,
∴AD=5,
∴由勾股定理知:OD===4,
∴点C的坐标是:(﹣5,4).
故答案为:(﹣5,4).
15.解:∵四边形ABCD是菱形,
∴AD=BC,AC⊥BD,AO=OC,DO=BO,
∵AC=8,BD=6,
∴AO=4,OD=3,由勾股定理得:AD=5,
∴BC=5,
∴S菱形ABCD=×AC×BD=BC×DE,
∴×6×8=5×DE,
解得:DE=,
故答案为:.
16.解:连接BD,如图所示:
∵E、F分别是AB,AD的中点,且EF=2,
∴EF是△ABD的中位线,
∴BD=2EF=2×2=4,
∵AC、BD是正方形ABCD的对角线,
∴AC=BD=4.
故答案为:4
17.解:∵四边形ABCD是矩形,
∴∠BCD=90°,OA=OC=OD=OB=BD=,
∵OE=1,CE⊥BD,
∴由勾股定理可知:CE=1,
故答案为:1.
18.解:∵△DCE是直角三角形,
∴△PBC为直角三角形,
∴点P只能在AB上或者CD上,
当点P在AB上时,有BP=CE,
∴BP=CE=1,
∴AP=2,
∴t=2÷1=2,
当点P在CD上时,有CP=CE=1,
∴t=(3+3+1)÷1=7,
故答案为:2或7.
三.解答题(共5小题,满分40分)
19.证明:∵PQ∥BC,
∴∠DEC=∠BCE,∠DFC=∠GCF,
∵CE平分∠BCA,CF平分∠ACG,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∴∠DEC=∠DCE,∠DFC=∠DCF,
∴DE=DC,DF=DC,
∴DE=DF,
∵点D是边AC的中点,
∴AD=CD,
∴四边形AECF是平行四边形,
∵∠BCA+∠ACG=180°,
∴∠ECF=∠DCE+∠DCF=×180°=90°,
∴平行四边形AECF是矩形.
20.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:∵四边形BNDM是菱形,
∴BM=BN=DM=DN,
设BN=DN=x,则CN=BC﹣BN=16﹣x,
在Rt△CDN中,由勾股定理得:CD2+CN2=DN2,
即82+(16﹣x)2=x2,
解得:x=10,
即BN=10,
∴菱形BNDM的周长=4BN=40.
21.解:(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°﹣∠GFH,∠DHE=180°﹣∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)解:作FG⊥BC于G,
∵四边形ABEF是菱形,若AE=2,BF=2,
∴AE⊥BF,OE=AE=1,OB=BF=,
∴BE==2,
∵S菱形ABEF= AE BF=BE FG,
∴GF=,
∴S平行四边形ABCD=BC FG=(BE+EC) GF=(2+1)×=3.
23.(1)证明:过O作OH⊥AB于H点,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的角平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF,
又四边形OGCF是矩形,
∴四边形OGCF是正方形;
(2)解:在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=90°﹣60°=30°,
∴AC=AB,
∵AC=4,
∴AB=2AC=2×4=8,
∵AC2+BC2=AB2,
∴BC==4,
在Rt△AOH和Rt△AOF中,
,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF的边长为x,
则AH=AF=4﹣x,BH=BG=4﹣x,
∴4﹣x+4﹣x=8,
∴x=2﹣2,
即正方形OGCF的边长为2﹣2.
一.选择题(共10小题,满分40分)
1.已知菱形的两条对角线的长分别为6cm和8cm,则这个菱形的面积是( )
A.20cm2 B.24cm2 C.48cm2 D.100cm2
2.如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ACDB是菱形的依据是( )
A.对角线互相垂直的平行四边形是菱形 B.对角线平分一组对角的四边形是菱形
C.一组邻边相等的四边形是菱形 D.四条边相等的四边形是菱形
3.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形 B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是正方形
4.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
5.如图,点E、F在矩形ABCD的对角线BD所在的直线上,BE=DF,则四边形AECF是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
6.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
7.如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE B.BE=AD﹣DF C.AB=AF D.AF=AD
8.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
9.数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得∠D=60°,对角线AC长为16cm,改变教具的形状成为图2所示的正方形,则正方形的边长为( )
A.8cm B.4cm C.16cm D.16cm
10.如图,矩形OABC的顶点O与原点重合,点A,C分别在x轴,y轴上,点B的坐标为(﹣5,4),点D为边BC上一动点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )
A.(﹣5,3) B.(﹣5,4) C.(﹣5,) D.(﹣5,2)
二.填空题(共8小题,满分40分)
11.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
12.如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于 .
13.已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
14.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是 .
15.如图,在菱形ABCD中,AC、BD相交于点O,DE⊥BC,垂足为E.若AC=8,BD=6,则DE的长为 .
16.如图,在正方形ABCD中,E,F分别是AB,AD的中点,若EF=2,则AC的长是 .
17.如图,矩形ABCD中,对角线AC与BD相交于点O,过点C作CE⊥BD,垂足为点E.若OE=1,BD=2.则CE= .
18.如图,在正方形ABCD中,AB=3cm,延长BC到点E,使CE=1cm,连接DE,动点P从点A出发,以每秒1cm的速度沿AB→BC→CD→DA向终点A运动.设点P的运动时间为t秒,当△PBC和△DCE全等时,t的值为 .
三.解答题(共5小题,满分40分)
19.如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.
20.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若∠C=90°,BC=16,CD=8,求菱形BNDM的周长.
21.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
22.如图,在 ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=2,BF=2,CE=1,求 ABCD的面积.
23.如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵菱形的两条对角线的长分别为6cm和8cm,
∴这个菱形的面积=×6×8=24(cm2),
故选:B.
2.解:由作图得:BA=BD,CA=CD,
∵AB=AC,
∴AB=AC=BD=CD,
∴四边形ACDB是菱形,
故选:D.
3.解:A、对角线互相平分的四边形是平行四边形,对角线相等的四边形也可能是等腰梯形等四边形,故A不符合题意;
B、对角线互相平分的四边形是平行四边形,若对角线再相等,则四边形是矩形,故B符合题意;
C、对角线互相垂直的四边形不能判定是平行四边形,也就不能判定是菱形,故C不符合题意;
D、对角线互相垂直平分的四边形是菱形,不能判断它的内角有直角,故D不符合题意;
故选:B.
4.解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
故选:B.
5.解:A.∵四边形ABCD是矩形,
∴AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形,
故本选项符合题意;
B.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是矩形,
故本选项不符合题意;
C.∵四边形ABCD是矩形,
∴不能证明AC⊥BD,
∴不能证明AC⊥EF,
故本选项不符合题意;
D.∵四边形ABCD是矩形,
∴AC=BD,
∴AC≠EF,
∴四边形AECF不是正方形,
故本选项不符合题意;
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
7.解:A、由矩形ABCD,AF⊥DE可得∠C=∠AFD=90°,AD∥BC,
∴∠ADF=∠DEC.
又∵DE=AD,
∴△AFD≌△DCE(AAS),故A正确;
B、由△AFD≌△DCE,可得CE=DF,
由矩形ABCD,可得BC=AD,
又∵BE=BC﹣EC,
∴BE=AD﹣DF,故B正确;
C、由△AFD≌△DCE,可得AF=CD,
由矩形ABCD,可得AB=CD,
∴AB=AF,故C正确;
D、∵∠ADF不一定等于30°,
∴直角三角形ADF中,AF不一定等于AD的一半,故D错误;
故选:D.
8.解:设AC交BD于O,
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB==5,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
9.解:如图1,图2中,连接AC.
图1中,∵四边形ABCD是菱形,
∴AD=DC,
∵∠D=60°,
∴△ADC是等边三角形,
∴AD=DC=AC=16cm,
∴正方形ABCD的边长为16cm,
故选:C.
10.解:由题可得,AO=BC=5,AB=CO=4,
由旋转可得,DE=OD,∠EDO=90°,
又∵∠B=∠OCD=90°,
∴∠EDB+∠CDO=90°=∠COD+∠CDO,
∴∠EDB=∠DOC,
∴△DBE≌△OCD(AAS),
∴BD=OC=4,
设AE=x,则BE=4﹣x=CD,
∵BD+CD=5,
∴4+4﹣x=5,
解得x=3,
∴AE=3,
∴E(﹣5,3),
故选:A.
二.填空题(共8小题,满分40分)
11.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
12.解:如图,连接CD.
∵∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
∵S△ABC=BC AC=AB CD,
∴×8×6=×10×CD,
解得CD=4.8,
∴EF=4.8.
故答案为:4.8.
13.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=4、CF=CD﹣DF=4﹣1=3,
∴BF==5,
∴GH=BF=,
故答案为:.
14.解:∵菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,
∴AB=5,
∴AD=5,
∴由勾股定理知:OD===4,
∴点C的坐标是:(﹣5,4).
故答案为:(﹣5,4).
15.解:∵四边形ABCD是菱形,
∴AD=BC,AC⊥BD,AO=OC,DO=BO,
∵AC=8,BD=6,
∴AO=4,OD=3,由勾股定理得:AD=5,
∴BC=5,
∴S菱形ABCD=×AC×BD=BC×DE,
∴×6×8=5×DE,
解得:DE=,
故答案为:.
16.解:连接BD,如图所示:
∵E、F分别是AB,AD的中点,且EF=2,
∴EF是△ABD的中位线,
∴BD=2EF=2×2=4,
∵AC、BD是正方形ABCD的对角线,
∴AC=BD=4.
故答案为:4
17.解:∵四边形ABCD是矩形,
∴∠BCD=90°,OA=OC=OD=OB=BD=,
∵OE=1,CE⊥BD,
∴由勾股定理可知:CE=1,
故答案为:1.
18.解:∵△DCE是直角三角形,
∴△PBC为直角三角形,
∴点P只能在AB上或者CD上,
当点P在AB上时,有BP=CE,
∴BP=CE=1,
∴AP=2,
∴t=2÷1=2,
当点P在CD上时,有CP=CE=1,
∴t=(3+3+1)÷1=7,
故答案为:2或7.
三.解答题(共5小题,满分40分)
19.证明:∵PQ∥BC,
∴∠DEC=∠BCE,∠DFC=∠GCF,
∵CE平分∠BCA,CF平分∠ACG,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∴∠DEC=∠DCE,∠DFC=∠DCF,
∴DE=DC,DF=DC,
∴DE=DF,
∵点D是边AC的中点,
∴AD=CD,
∴四边形AECF是平行四边形,
∵∠BCA+∠ACG=180°,
∴∠ECF=∠DCE+∠DCF=×180°=90°,
∴平行四边形AECF是矩形.
20.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:∵四边形BNDM是菱形,
∴BM=BN=DM=DN,
设BN=DN=x,则CN=BC﹣BN=16﹣x,
在Rt△CDN中,由勾股定理得:CD2+CN2=DN2,
即82+(16﹣x)2=x2,
解得:x=10,
即BN=10,
∴菱形BNDM的周长=4BN=40.
21.解:(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°﹣∠GFH,∠DHE=180°﹣∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)解:作FG⊥BC于G,
∵四边形ABEF是菱形,若AE=2,BF=2,
∴AE⊥BF,OE=AE=1,OB=BF=,
∴BE==2,
∵S菱形ABEF= AE BF=BE FG,
∴GF=,
∴S平行四边形ABCD=BC FG=(BE+EC) GF=(2+1)×=3.
23.(1)证明:过O作OH⊥AB于H点,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的角平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF,
又四边形OGCF是矩形,
∴四边形OGCF是正方形;
(2)解:在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=90°﹣60°=30°,
∴AC=AB,
∵AC=4,
∴AB=2AC=2×4=8,
∵AC2+BC2=AB2,
∴BC==4,
在Rt△AOH和Rt△AOF中,
,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF的边长为x,
则AH=AF=4﹣x,BH=BG=4﹣x,
∴4﹣x+4﹣x=8,
∴x=2﹣2,
即正方形OGCF的边长为2﹣2.
