2021-2022学年人教版数学七年级下册5.2平行线及其判定课堂提高训练试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.2平行线及其判定课堂提高训练试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 76.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 18:47:18 | ||
图片预览



文档简介
2022年春人教版初中七年级下册数学课堂提高训练试卷
班级 姓名
第5章 相交线与平行线
5.2 平行线及其判定
一.选择题(共36分)
1.下列说法正确的是( )
A.不相交的两条直线叫做平行线
B.同一平面内,过一点有且仅有一条直线与已知直线垂直
C.平角是一条直线
D.过同一平面内三点中任意两点,只能画出3条直线
2.下列说法正确的个数是( )
①同位角相等;
②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;
④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
A.1个 B.2个 C.3个 D.4个
3.过直线l外一点A作l的平行线,可以作( )条.
A.1 B.2 C.3 D.4
4.已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
5.有下列说法:①两条不相交的直线叫平行线;②同一平面内,过一点有且只有一条直线与已知直线垂直;③两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线互相垂直;④有公共顶点的两个角是对顶角.其中说法正确的个数是( )
A.1 B.2 C.3 D.4
6.下列说法中正确的是( )
A.角是由两条射线组成的图形
B.如果线段AB=BC,那么B叫做线段AB的中点
C.在同一平面内,没有公共点的两条直线是平行线
D.一条射线就是一个周角
7.平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
A.只有① B.只有②
C.①②都正确 D.①②都不正确
8.如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠4=∠5;③∠8=∠1;④∠6+∠7=180°.其中,能够判断a∥b的是( )
A.①②③④ B.①③ C.②③④ D.①②
9.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
10.如果a∥b,b∥c,那么a∥c,这个推理的依据是( )
A.等量代换
B.两直线平行,同位角相等
C.平行公理
D.平行于同一直线的两条直线平行
11.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
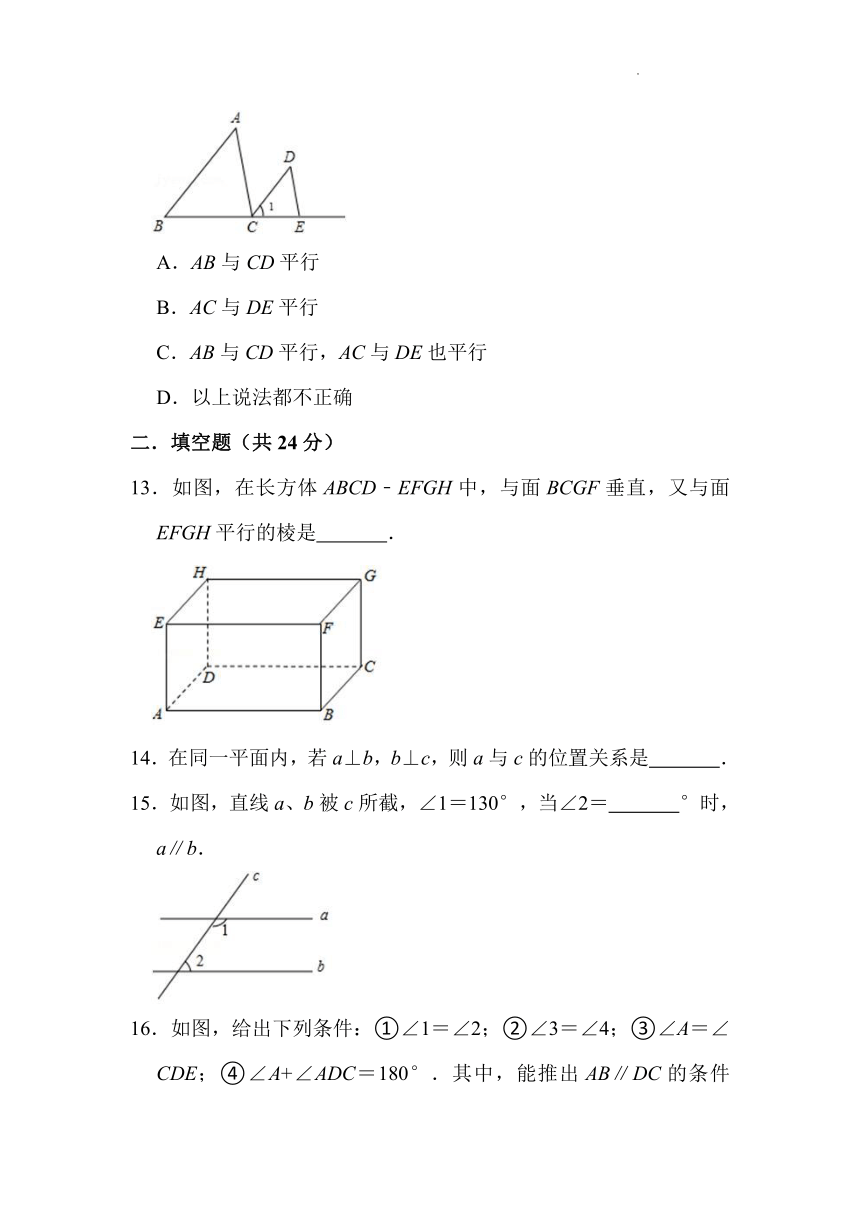
12.已知:如图所示,∠1=∠B,则下列说法正确的是( )
A.AB与CD平行
B.AC与DE平行
C.AB与CD平行,AC与DE也平行
D.以上说法都不正确
二.填空题(共24分)
13.如图,在长方体ABCD﹣EFGH中,与面BCGF垂直,又与面EFGH平行的棱是 .
14.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 .
15.如图,直线a、b被c所截,∠1=130°,当∠2= °时,a∥b.
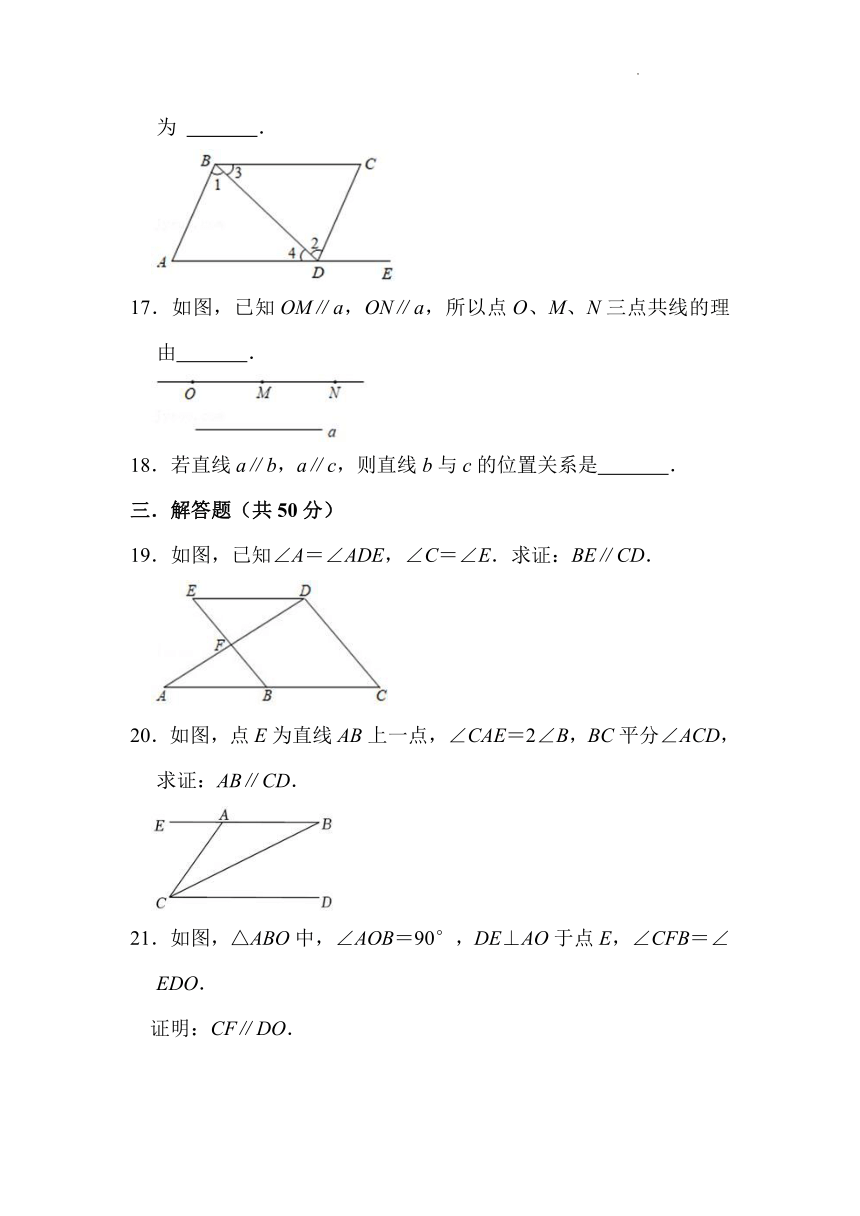
16.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为 .
17.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
18.若直线a∥b,a∥c,则直线b与c的位置关系是 .
三.解答题(共50分)
19.如图,已知∠A=∠ADE,∠C=∠E.求证:BE∥CD.
20.如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
21.如图,△ABO中,∠AOB=90°,DE⊥AO于点E,∠CFB=∠EDO.
证明:CF∥DO.
22.已知:如图,CB平分∠ACD,交AE于点B,且AB=AC.求证:AE∥CD.
23.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.
求证:DE∥BC.
参考答案
一.选择题
1.B; 2.A; 3.A; 4.D; 5.A; 6.C; 7.A; 8.A; 9.B; 10.D; 11.C; 12.A;
二.填空题
13.棱AB,棱CD;
14.a∥c;
15.50;
16.①③④;
17.经过直线外一点,有且只有一条直线与这条直线平行;
18.平行;
三.解答题
19.证明: ∵∠A=∠ADE,
∴DE// AC,
∴∠ABE=∠E,
又∵∠C=∠E,
∴∠ABE=∠C,
∴BE//CD .;
20.证明:由题意知∠CAE=∠ACB+∠B (三角形外角的性质),
∵∠CAE=2∠B (已知) ,
∴∠B=∠ACB (等量代换),
又"∵BC平分∠ACD (已知) ,
∴∠ACB=∠DCB (角平分线的定义),
∴∠B=∠DCB (等量代换),
∴AB//CD (内错角相等,两直线平行) .;
21.证明: ∵DE⊥AO,
∠A ED=90°,
∴∠AED=∠AOB=90°,
∴DE/ BO,
∴∠EDO=∠BOD,
∵∠EDO=∠CFB,
∴∠BOD=∠CFB, .
∴CF //DO .;
22.证明: ∵AB=AC,
∴∠ABC=∠ACB,
∵CB平分∠ACD,
∴∠ACB=∠BCD, .
∴∠ABC=∠BCD,
∴AE// CD .;
23.]证明: ∵∠BDC+∠DHF= 180°
∴BD// FH,
∴∠B=∠EFC,
∵∠DEF=∠B,
∴∠EFC=∠DEF,
∴DE// BC .;
班级 姓名
第5章 相交线与平行线
5.2 平行线及其判定
一.选择题(共36分)
1.下列说法正确的是( )
A.不相交的两条直线叫做平行线
B.同一平面内,过一点有且仅有一条直线与已知直线垂直
C.平角是一条直线
D.过同一平面内三点中任意两点,只能画出3条直线
2.下列说法正确的个数是( )
①同位角相等;
②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;
④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
A.1个 B.2个 C.3个 D.4个
3.过直线l外一点A作l的平行线,可以作( )条.
A.1 B.2 C.3 D.4
4.已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
5.有下列说法:①两条不相交的直线叫平行线;②同一平面内,过一点有且只有一条直线与已知直线垂直;③两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线互相垂直;④有公共顶点的两个角是对顶角.其中说法正确的个数是( )
A.1 B.2 C.3 D.4
6.下列说法中正确的是( )
A.角是由两条射线组成的图形
B.如果线段AB=BC,那么B叫做线段AB的中点
C.在同一平面内,没有公共点的两条直线是平行线
D.一条射线就是一个周角
7.平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
A.只有① B.只有②
C.①②都正确 D.①②都不正确
8.如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠4=∠5;③∠8=∠1;④∠6+∠7=180°.其中,能够判断a∥b的是( )
A.①②③④ B.①③ C.②③④ D.①②
9.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
10.如果a∥b,b∥c,那么a∥c,这个推理的依据是( )
A.等量代换
B.两直线平行,同位角相等
C.平行公理
D.平行于同一直线的两条直线平行
11.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
12.已知:如图所示,∠1=∠B,则下列说法正确的是( )
A.AB与CD平行
B.AC与DE平行
C.AB与CD平行,AC与DE也平行
D.以上说法都不正确
二.填空题(共24分)
13.如图,在长方体ABCD﹣EFGH中,与面BCGF垂直,又与面EFGH平行的棱是 .
14.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 .
15.如图,直线a、b被c所截,∠1=130°,当∠2= °时,a∥b.
16.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为 .
17.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
18.若直线a∥b,a∥c,则直线b与c的位置关系是 .
三.解答题(共50分)
19.如图,已知∠A=∠ADE,∠C=∠E.求证:BE∥CD.
20.如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
21.如图,△ABO中,∠AOB=90°,DE⊥AO于点E,∠CFB=∠EDO.
证明:CF∥DO.
22.已知:如图,CB平分∠ACD,交AE于点B,且AB=AC.求证:AE∥CD.
23.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.
求证:DE∥BC.
参考答案
一.选择题
1.B; 2.A; 3.A; 4.D; 5.A; 6.C; 7.A; 8.A; 9.B; 10.D; 11.C; 12.A;
二.填空题
13.棱AB,棱CD;
14.a∥c;
15.50;
16.①③④;
17.经过直线外一点,有且只有一条直线与这条直线平行;
18.平行;
三.解答题
19.证明: ∵∠A=∠ADE,
∴DE// AC,
∴∠ABE=∠E,
又∵∠C=∠E,
∴∠ABE=∠C,
∴BE//CD .;
20.证明:由题意知∠CAE=∠ACB+∠B (三角形外角的性质),
∵∠CAE=2∠B (已知) ,
∴∠B=∠ACB (等量代换),
又"∵BC平分∠ACD (已知) ,
∴∠ACB=∠DCB (角平分线的定义),
∴∠B=∠DCB (等量代换),
∴AB//CD (内错角相等,两直线平行) .;
21.证明: ∵DE⊥AO,
∠A ED=90°,
∴∠AED=∠AOB=90°,
∴DE/ BO,
∴∠EDO=∠BOD,
∵∠EDO=∠CFB,
∴∠BOD=∠CFB, .
∴CF //DO .;
22.证明: ∵AB=AC,
∴∠ABC=∠ACB,
∵CB平分∠ACD,
∴∠ACB=∠BCD, .
∴∠ABC=∠BCD,
∴AE// CD .;
23.]证明: ∵∠BDC+∠DHF= 180°
∴BD// FH,
∴∠B=∠EFC,
∵∠DEF=∠B,
∴∠EFC=∠DEF,
∴DE// BC .;
