2021-2022学年青岛版 八年级数学下册6.4三角形的中位线定理 课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年青岛版 八年级数学下册6.4三角形的中位线定理 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 592.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 20:43:03 | ||
图片预览



文档简介
(共14张PPT)
6.4 三角形的中位线定理
学习目标
1. 知道三角形中位线的概念;能说出三 角形中位线的性质定理及其证明方法;
2. 能运用三角形中位线定理解决与之相关的问题。
1.通读课本P30-32,标注出本节课的知识点;
2.结合学案和课件,思考定理的符号语言、证明方法
3.完成对应练习和达标检测题
学习要求
E
D
A
B
C
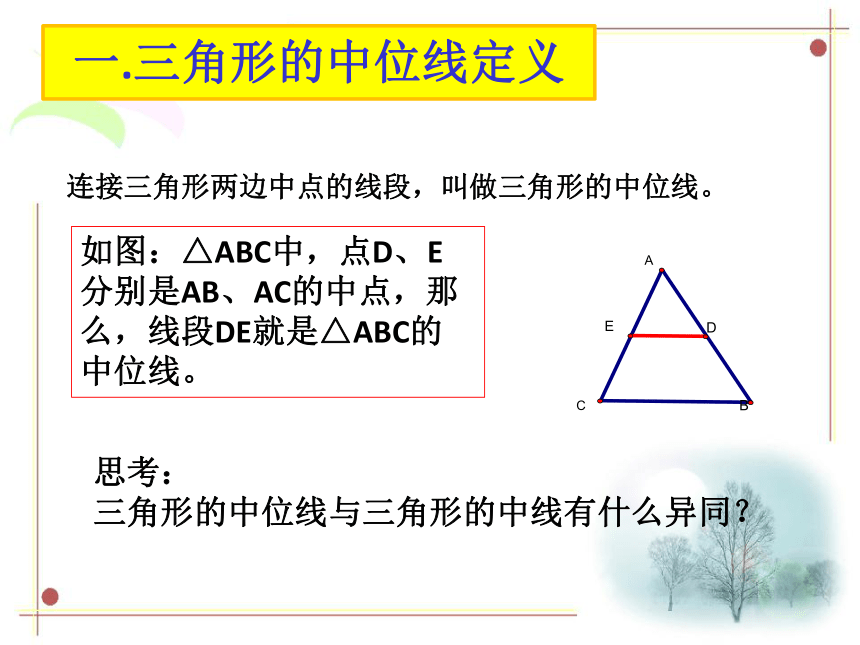
一.三角形的中位线定义
连接三角形两边中点的线段,叫做三角形的中位线。
思考:
三角形的中位线与三角形的中线有什么异同?
如图:△ABC中,点D、E分别是AB、AC的中点,那么,线段DE就是△ABC的中位线。
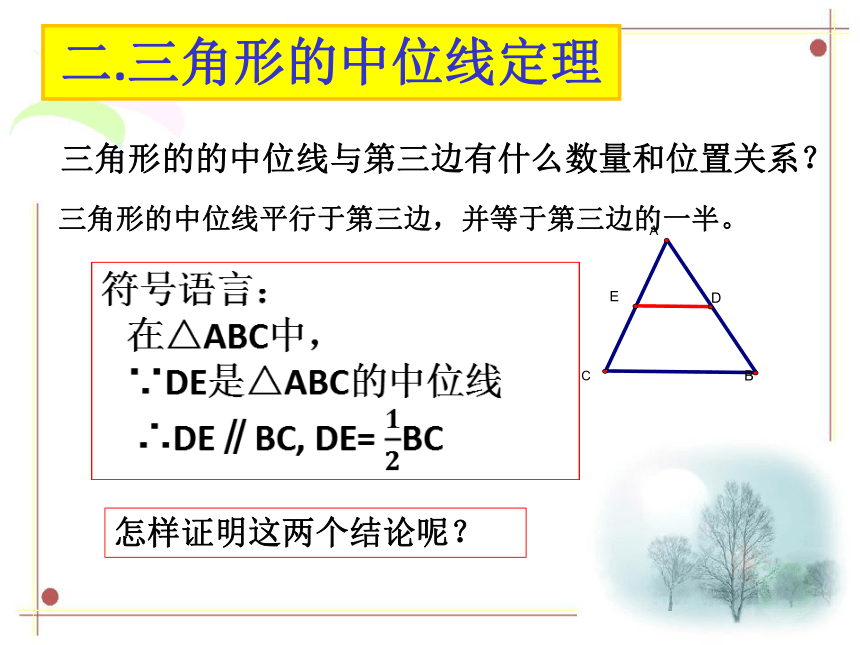
二.三角形的中位线定理
E
D
A
B
C
三角形的的中位线与第三边有什么数量和位置关系?
三角形的中位线平行于第三边,并等于第三边的一半。
怎样证明这两个结论呢?
F
E
D
C
B
A
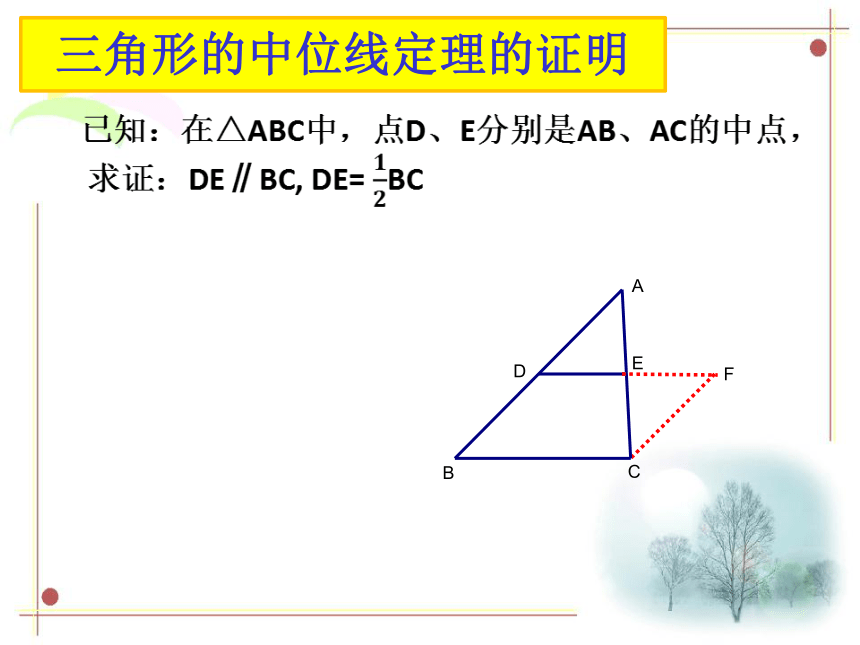
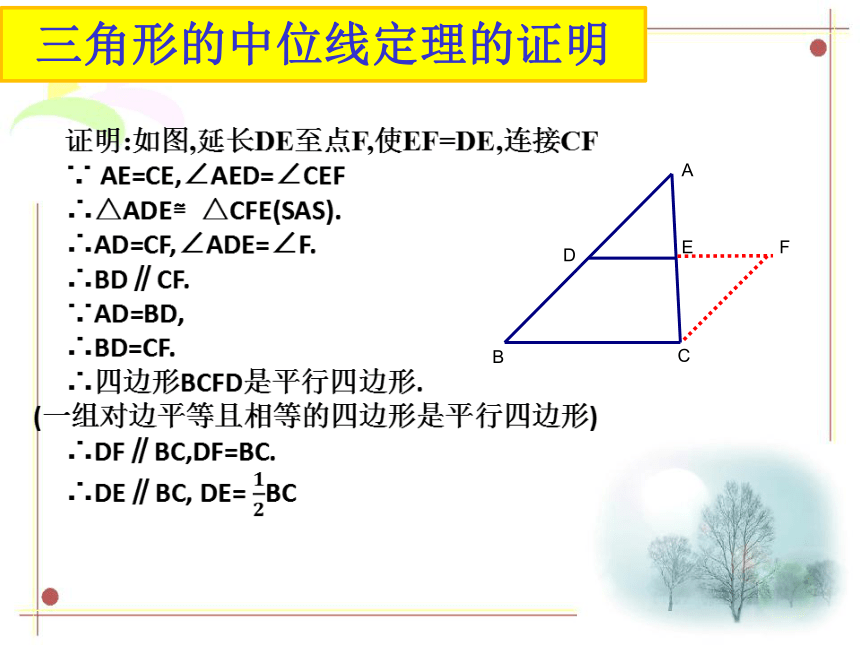
三角形的中位线定理的证明
F
E
D
C
B
A
三角形的中位线定理的证明
三角形的中位线平行于第三边,并等于第三边的一半。
归纳总结
三角形中位线定理:
(1)如图,AB是池塘两端,设计一方案测量AB的距离,首先取一点C,连接AC,BC,再取它们的中点D,E,测得DE=15米,则AB= 米.
小试牛刀
(2)如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
A.3 B.4 C.5 D.6
30
B
学以致用
思考:
什么是中点四边形?
四边形的中点四边形是什么形状的呢?
它的形状与原四边形有什么关系呢?
例题:
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形。
原四边形的特征 中点四边形的形状
①对角线相等的四边形
②对角线互相垂直的四边形
③对角线相等且互相垂直的四边形
完成下面表格:
归纳总结
菱形
矩形
正方形
1.若顺次连接四边形四边中点所得的四边形是菱形,则原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
小试身手
D
2.如图,E、F、G、H分别是BD、BC、AC、AD的中点,又AB=DC,下列结论:①EFGH为矩形;②FH平分EG于T;③EG⊥FH;④HF平分∠EHG.其中正确的是( )
A、①和② B、②和③
C、①②④ D、②③④
D
知识梳理
同学们,今天我们学习了哪些内容?把你的收获写下来吧。
布置作业
完成综训6.4的题目。
6.4 三角形的中位线定理
学习目标
1. 知道三角形中位线的概念;能说出三 角形中位线的性质定理及其证明方法;
2. 能运用三角形中位线定理解决与之相关的问题。
1.通读课本P30-32,标注出本节课的知识点;
2.结合学案和课件,思考定理的符号语言、证明方法
3.完成对应练习和达标检测题
学习要求
E
D
A
B
C
一.三角形的中位线定义
连接三角形两边中点的线段,叫做三角形的中位线。
思考:
三角形的中位线与三角形的中线有什么异同?
如图:△ABC中,点D、E分别是AB、AC的中点,那么,线段DE就是△ABC的中位线。
二.三角形的中位线定理
E
D
A
B
C
三角形的的中位线与第三边有什么数量和位置关系?
三角形的中位线平行于第三边,并等于第三边的一半。
怎样证明这两个结论呢?
F
E
D
C
B
A
三角形的中位线定理的证明
F
E
D
C
B
A
三角形的中位线定理的证明
三角形的中位线平行于第三边,并等于第三边的一半。
归纳总结
三角形中位线定理:
(1)如图,AB是池塘两端,设计一方案测量AB的距离,首先取一点C,连接AC,BC,再取它们的中点D,E,测得DE=15米,则AB= 米.
小试牛刀
(2)如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
A.3 B.4 C.5 D.6
30
B
学以致用
思考:
什么是中点四边形?
四边形的中点四边形是什么形状的呢?
它的形状与原四边形有什么关系呢?
例题:
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形。
原四边形的特征 中点四边形的形状
①对角线相等的四边形
②对角线互相垂直的四边形
③对角线相等且互相垂直的四边形
完成下面表格:
归纳总结
菱形
矩形
正方形
1.若顺次连接四边形四边中点所得的四边形是菱形,则原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
小试身手
D
2.如图,E、F、G、H分别是BD、BC、AC、AD的中点,又AB=DC,下列结论:①EFGH为矩形;②FH平分EG于T;③EG⊥FH;④HF平分∠EHG.其中正确的是( )
A、①和② B、②和③
C、①②④ D、②③④
D
知识梳理
同学们,今天我们学习了哪些内容?把你的收获写下来吧。
布置作业
完成综训6.4的题目。
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
