2022届高考数学三轮冲刺课-第1讲焦点三角形中的秒杀技巧课件(34张ppt)
文档属性
| 名称 | 2022届高考数学三轮冲刺课-第1讲焦点三角形中的秒杀技巧课件(34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 15:27:26 | ||
图片预览









文档简介
(共34张PPT)
高考数学冲刺(1)
焦点三角形中的秒杀技巧
主讲人: |
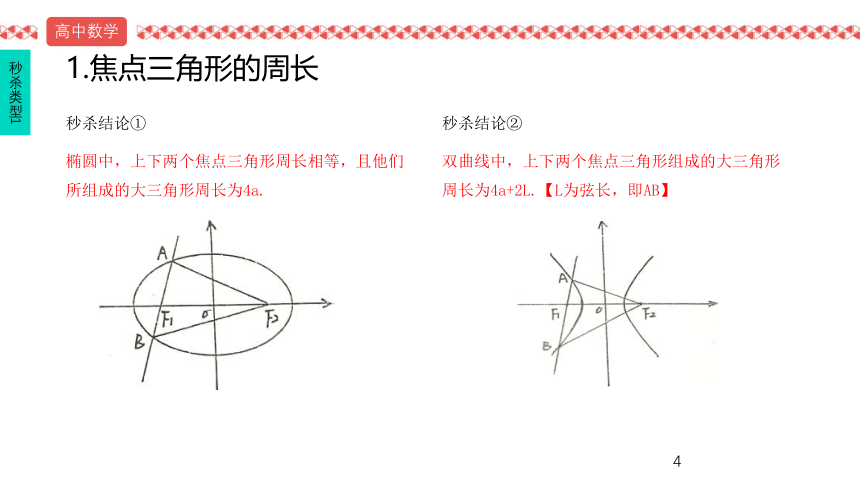
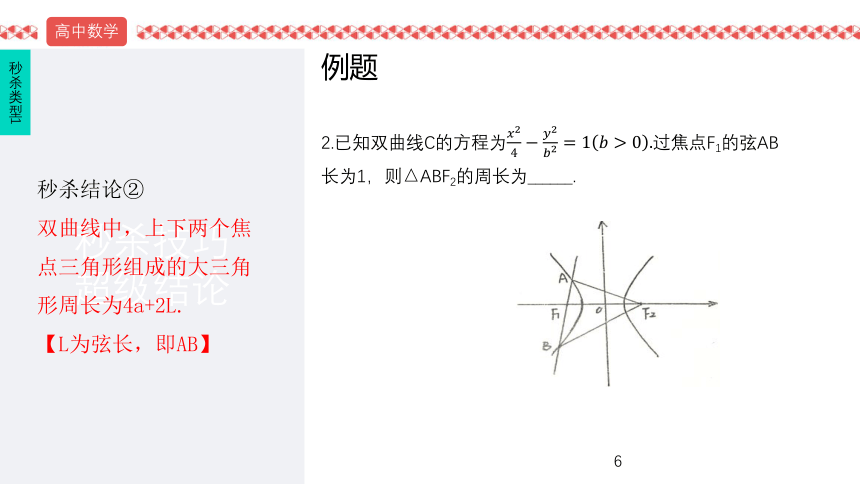
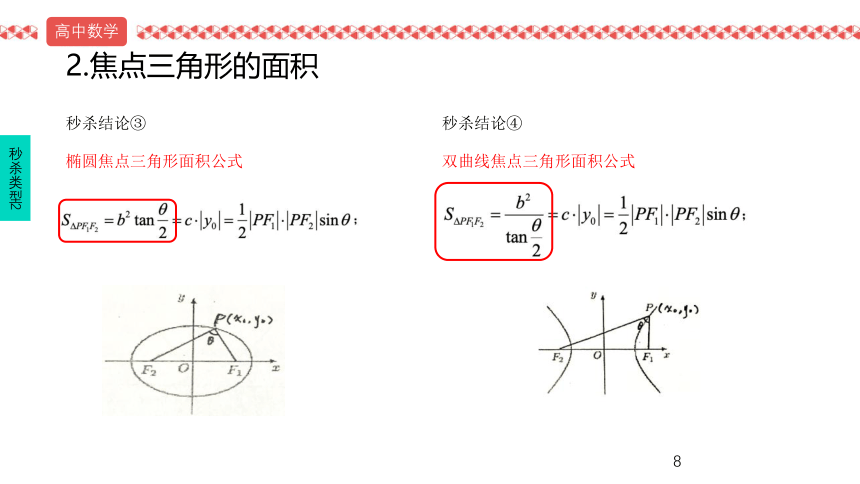
01圆锥焦点三角形中的秒杀结论02圆锥焦点、通径、渐近线秒杀技巧03圆锥中点弦模型04函数奇偶性、单调性、周期性秒杀技巧05综合线性规划、二项式、不等式秒杀06数列列举法秒杀数列07数列数列四大求和方法08综合排列组合七大解题策略09函数函数值域技巧、数形结合技巧10综合巧解高考小题本节说明5个类型,9个小结论焦点三角形的周长★焦点三角形的面积★ ★ ★焦点三角形和离心率★ ★ ★焦点三角形的角平分线和内切圆★ ★焦点三角形的中位线和内切圆★ ★秒杀类型1秒杀类型2秒杀类型3秒杀类型4秒杀类型51.焦点三角形的周长秒杀结论①椭圆中,上下两个焦点三角形周长相等,且他们所组成的大三角形周长为4a.秒杀结论②双曲线中,上下两个焦点三角形组成的大三角形周长为4a+2L.【L为弦长,即AB】秒杀类型1例题秒杀类型1秒杀结论①椭圆中,上下两个焦点三角形周长相等,且他们所组成的大三角形周长为4a.1.(全国课标卷)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为,过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为____________________________________。例题2.已知双曲线C的方程为过焦点F1的弦AB长为1,则△ABF2的周长为______.秒杀类型1秒杀结论②双曲线中,上下两个焦点三角形组成的大三角形周长为4a+2L.【L为弦长,即AB】练习1.(湖北)过双曲线左焦点F1的直线交曲线的左支于M,N两点,F2为其右焦点,则|MF2|+|NF2|-|MN|的值为_________.秒杀类型12.焦点三角形的面积秒杀结论③椭圆焦点三角形面积公式秒杀结论④双曲线焦点三角形面积公式秒杀类型2例题1.(上海)已知F1,F2是椭圆C:的两个焦点,P为椭圆C上一点,且,若△PF1F2的面积为9,则b=________.秒杀结论③秒杀类型2例题2.(全国)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=().A.2 B.4 C.6 D.8秒杀结论④秒杀类型2练习1.(全国三卷)已知双曲线的焦点为F1,F2,点M在双曲线上且,点M到x轴的距离为().2.(全国一卷)已知M(x0,y0)是双曲线C:上的一点,F1,F2是C上的两个焦点,若,则y0的取值范围是().秒杀类型2练习3.(全国卷)双曲线的两个焦点为F1,F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为______.4.(全国卷)椭圆的焦点为F1,F2,点P为其上的动点,当∠F1PF2为钝角时,点P的横坐标取值范围是________.秒杀类型2练习5.(广东六校第三次联考)设F1,F2是双曲线的两个焦点,P是双曲线上一点,且3|PF1|=4|PF2|,则△PF1F2的面积为().6.(河南部分重点中学联考)如图,已知椭圆C的中心为原点O,F为C的左焦点,P为C上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C的方程为().秒杀类型23.焦点三角形和离心率秒杀结论⑤在同一个坐标系内,若椭圆和双曲线有共同的焦点F1,F2,则把它们称为一组“交通线”(焦同线).椭圆的离心率e1,双曲线的离心率e2,P是他们的一个公共点,∠F1PF2=θ,则有:若θ=90°,则有:秒杀类型3例题1.(浙江卷)如图,F1,F2是椭圆C1:与双曲线C2的公共焦点,A和B分别是C1,C2在第二、第四象限内的公共点。若四边形AF1BF2为矩形,则C2的离心率是()秒杀结论⑤交通线秒杀类型3练习1.我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F1、F2是一对相关曲线的焦点,P是它们在第一象限的交点,当∠F1PF2=60°时,这一对相关曲线中双曲线的离心率是().2.(浙江卷)已知椭圆C1:与双曲线C2:的焦点重合,e1,e2分别为C1,C2的离心率,则().秒杀类型3解析2.m>n可以根据图像直接得出,首先排除C和D.由于m和n都是未知的,所以题目中的交通线存在无数种可能,故它们的公共焦点三角形也存在无数种可能,我们不妨选取一种特殊的情形:焦点三角形恰好为直角三角形,即θ=90°,这样根据秒杀结论有:因为m>n,所以分子括号内为正,分子整体>2;分子>2,整个分数=2,故分母必须>1,选A.秒杀类型3例题2.(湖北卷)已知F1,F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=,则椭圆和双曲线的离心率的倒数之和的最大值为().秒杀结论⑤交通线秒杀类型3解析解析:根据秒杀结论⑤,当θ=60°时,套入公式并调整格式:.接下来就是一个不等式问题.本题中,当时取最大,可以算出e1和e2,此时,故选A.秒杀类型3练习3.(甘肃模拟)已知椭圆和双曲线有共同的焦点F1和F2,P是他们的一个焦点,且∠F1PF2=60°,记椭圆和双曲线的离心率分别为e1,e2,则当取最大值时,e1和e2的值分别是().秒杀类型33.焦点三角形和离心率秒杀结论⑥椭圆焦点三角形△PF1F2的底角为α和β,则离心率秒杀结论⑥如果是双曲线,则离心率秒杀类型3例题1.(全国二卷)设椭圆C:的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为().秒杀类型3秒杀结论⑥椭圆用+,双曲线用-例题2.(全国二卷)已知F1,F2是双曲线E:的左、右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为().秒杀类型3秒杀结论⑥椭圆用+,双曲线用-练习1.(辽宁卷)已知椭圆的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF。若AB=10,BF=8,cos∠ABF=,则C的离心率为().2.(温州瑞安四校联考第二次月考)设F1,F2是双曲线(a>b>0)的两个焦点,若双曲线上存在一点P,使∠PF1F2=30°,∠PF2F1=120°,则双曲线的离心率为().秒杀类型3练习3.(福建卷)椭圆C:的左、右焦点分别为F1,F2,焦距为2c,与椭圆C的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于_______.4.(安徽安庆二模)已知F1,F2为双曲线的焦点,过F2作垂直于实轴的直线交双曲线于A,B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线离心率为().A.B.C.D.秒杀类型3练习5.(全国卷)设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,AB为C的实轴长的2倍,则C的离心率为().6.(太原三模)设F1,F2是双曲线E:的左、右焦点,P是双曲线右支上一点,满足(O是坐标原点),且3|PF1|=4|PF2|,则双曲线的离心率为().秒杀类型34.焦点三角形的角平分线和内切圆秒杀结论⑦AD是△ABC的角平分线,则:秒杀结论⑧椭圆焦点三角形面积S,它的内切圆半径为r,则:如果是双曲线,分母中“+”改为“-”。秒杀类型4例题1.(安徽卷)已知F1,F2为椭圆的焦点,点A(2,3)在椭圆上,求∠F1AF2的角平分线所在直线l的方程.秒杀类型4秒杀结论⑦例题2.(江苏模拟)已知椭圆的左右焦点为F1,F2,P是椭圆上的一点,△PF1F2的内切圆圆心为I,延长直线PI交x轴于点B,若椭圆的离心率为e,则PI:IB=().秒杀类型4秒杀结论⑧如果是双曲线,分母中“+”改为“-”。练习1.(全国一卷)已知F1,F2分别为双曲线C:的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2的角平分线,则AF2=_______.2.(福建莆田月考)已知点P是双曲线右支上一点,F1,F2分别为双曲线的左右焦点,I为△PF1F2的内心,若成立,则的值是().秒杀类型45.焦点三角形的中位线和内切圆秒杀结论⑨G、E、H三点共圆(圆心为F),且半径恒定:FG=FE=FH=aD:内接圆圆心F:原点G:A点到CD的垂足H:B点到CD的垂足E:D点到x轴的垂足(也是双曲线右顶点,也是内切圆与x轴的切点)秒杀类型5例题1.(重庆巴蜀中学)已知O为坐标原点,已知F1,F2是双曲线的两个焦点.P是双曲线右支上一点,PM为∠F1PF2的角平分线,过F1作PM的垂线交PM于点M,则OM的长度为().秒杀类型5秒杀结论⑨FG=FE=FH=a练习1.(太原二模)已知双曲线的左右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是().秒杀类型5练习2.(银川一中三模)设P是双曲线上除顶点外的任意一点,F1,F2分别是双曲线的左、右焦点,△PF1F2的内切圆与边F1F2相切于点M,则F1M·MF2=().A.5 B.4 C.2 D.1秒杀类型5
高考数学冲刺(1)
焦点三角形中的秒杀技巧
主讲人: |
01圆锥焦点三角形中的秒杀结论02圆锥焦点、通径、渐近线秒杀技巧03圆锥中点弦模型04函数奇偶性、单调性、周期性秒杀技巧05综合线性规划、二项式、不等式秒杀06数列列举法秒杀数列07数列数列四大求和方法08综合排列组合七大解题策略09函数函数值域技巧、数形结合技巧10综合巧解高考小题本节说明5个类型,9个小结论焦点三角形的周长★焦点三角形的面积★ ★ ★焦点三角形和离心率★ ★ ★焦点三角形的角平分线和内切圆★ ★焦点三角形的中位线和内切圆★ ★秒杀类型1秒杀类型2秒杀类型3秒杀类型4秒杀类型51.焦点三角形的周长秒杀结论①椭圆中,上下两个焦点三角形周长相等,且他们所组成的大三角形周长为4a.秒杀结论②双曲线中,上下两个焦点三角形组成的大三角形周长为4a+2L.【L为弦长,即AB】秒杀类型1例题秒杀类型1秒杀结论①椭圆中,上下两个焦点三角形周长相等,且他们所组成的大三角形周长为4a.1.(全国课标卷)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为,过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为____________________________________。例题2.已知双曲线C的方程为过焦点F1的弦AB长为1,则△ABF2的周长为______.秒杀类型1秒杀结论②双曲线中,上下两个焦点三角形组成的大三角形周长为4a+2L.【L为弦长,即AB】练习1.(湖北)过双曲线左焦点F1的直线交曲线的左支于M,N两点,F2为其右焦点,则|MF2|+|NF2|-|MN|的值为_________.秒杀类型12.焦点三角形的面积秒杀结论③椭圆焦点三角形面积公式秒杀结论④双曲线焦点三角形面积公式秒杀类型2例题1.(上海)已知F1,F2是椭圆C:的两个焦点,P为椭圆C上一点,且,若△PF1F2的面积为9,则b=________.秒杀结论③秒杀类型2例题2.(全国)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=().A.2 B.4 C.6 D.8秒杀结论④秒杀类型2练习1.(全国三卷)已知双曲线的焦点为F1,F2,点M在双曲线上且,点M到x轴的距离为().2.(全国一卷)已知M(x0,y0)是双曲线C:上的一点,F1,F2是C上的两个焦点,若,则y0的取值范围是().秒杀类型2练习3.(全国卷)双曲线的两个焦点为F1,F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为______.4.(全国卷)椭圆的焦点为F1,F2,点P为其上的动点,当∠F1PF2为钝角时,点P的横坐标取值范围是________.秒杀类型2练习5.(广东六校第三次联考)设F1,F2是双曲线的两个焦点,P是双曲线上一点,且3|PF1|=4|PF2|,则△PF1F2的面积为().6.(河南部分重点中学联考)如图,已知椭圆C的中心为原点O,F为C的左焦点,P为C上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C的方程为().秒杀类型23.焦点三角形和离心率秒杀结论⑤在同一个坐标系内,若椭圆和双曲线有共同的焦点F1,F2,则把它们称为一组“交通线”(焦同线).椭圆的离心率e1,双曲线的离心率e2,P是他们的一个公共点,∠F1PF2=θ,则有:若θ=90°,则有:秒杀类型3例题1.(浙江卷)如图,F1,F2是椭圆C1:与双曲线C2的公共焦点,A和B分别是C1,C2在第二、第四象限内的公共点。若四边形AF1BF2为矩形,则C2的离心率是()秒杀结论⑤交通线秒杀类型3练习1.我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F1、F2是一对相关曲线的焦点,P是它们在第一象限的交点,当∠F1PF2=60°时,这一对相关曲线中双曲线的离心率是().2.(浙江卷)已知椭圆C1:与双曲线C2:的焦点重合,e1,e2分别为C1,C2的离心率,则().秒杀类型3解析2.m>n可以根据图像直接得出,首先排除C和D.由于m和n都是未知的,所以题目中的交通线存在无数种可能,故它们的公共焦点三角形也存在无数种可能,我们不妨选取一种特殊的情形:焦点三角形恰好为直角三角形,即θ=90°,这样根据秒杀结论有:因为m>n,所以分子括号内为正,分子整体>2;分子>2,整个分数=2,故分母必须>1,选A.秒杀类型3例题2.(湖北卷)已知F1,F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=,则椭圆和双曲线的离心率的倒数之和的最大值为().秒杀结论⑤交通线秒杀类型3解析解析:根据秒杀结论⑤,当θ=60°时,套入公式并调整格式:.接下来就是一个不等式问题.本题中,当时取最大,可以算出e1和e2,此时,故选A.秒杀类型3练习3.(甘肃模拟)已知椭圆和双曲线有共同的焦点F1和F2,P是他们的一个焦点,且∠F1PF2=60°,记椭圆和双曲线的离心率分别为e1,e2,则当取最大值时,e1和e2的值分别是().秒杀类型33.焦点三角形和离心率秒杀结论⑥椭圆焦点三角形△PF1F2的底角为α和β,则离心率秒杀结论⑥如果是双曲线,则离心率秒杀类型3例题1.(全国二卷)设椭圆C:的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为().秒杀类型3秒杀结论⑥椭圆用+,双曲线用-例题2.(全国二卷)已知F1,F2是双曲线E:的左、右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为().秒杀类型3秒杀结论⑥椭圆用+,双曲线用-练习1.(辽宁卷)已知椭圆的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF。若AB=10,BF=8,cos∠ABF=,则C的离心率为().2.(温州瑞安四校联考第二次月考)设F1,F2是双曲线(a>b>0)的两个焦点,若双曲线上存在一点P,使∠PF1F2=30°,∠PF2F1=120°,则双曲线的离心率为().秒杀类型3练习3.(福建卷)椭圆C:的左、右焦点分别为F1,F2,焦距为2c,与椭圆C的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于_______.4.(安徽安庆二模)已知F1,F2为双曲线的焦点,过F2作垂直于实轴的直线交双曲线于A,B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线离心率为().A.B.C.D.秒杀类型3练习5.(全国卷)设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,AB为C的实轴长的2倍,则C的离心率为().6.(太原三模)设F1,F2是双曲线E:的左、右焦点,P是双曲线右支上一点,满足(O是坐标原点),且3|PF1|=4|PF2|,则双曲线的离心率为().秒杀类型34.焦点三角形的角平分线和内切圆秒杀结论⑦AD是△ABC的角平分线,则:秒杀结论⑧椭圆焦点三角形面积S,它的内切圆半径为r,则:如果是双曲线,分母中“+”改为“-”。秒杀类型4例题1.(安徽卷)已知F1,F2为椭圆的焦点,点A(2,3)在椭圆上,求∠F1AF2的角平分线所在直线l的方程.秒杀类型4秒杀结论⑦例题2.(江苏模拟)已知椭圆的左右焦点为F1,F2,P是椭圆上的一点,△PF1F2的内切圆圆心为I,延长直线PI交x轴于点B,若椭圆的离心率为e,则PI:IB=().秒杀类型4秒杀结论⑧如果是双曲线,分母中“+”改为“-”。练习1.(全国一卷)已知F1,F2分别为双曲线C:的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2的角平分线,则AF2=_______.2.(福建莆田月考)已知点P是双曲线右支上一点,F1,F2分别为双曲线的左右焦点,I为△PF1F2的内心,若成立,则的值是().秒杀类型45.焦点三角形的中位线和内切圆秒杀结论⑨G、E、H三点共圆(圆心为F),且半径恒定:FG=FE=FH=aD:内接圆圆心F:原点G:A点到CD的垂足H:B点到CD的垂足E:D点到x轴的垂足(也是双曲线右顶点,也是内切圆与x轴的切点)秒杀类型5例题1.(重庆巴蜀中学)已知O为坐标原点,已知F1,F2是双曲线的两个焦点.P是双曲线右支上一点,PM为∠F1PF2的角平分线,过F1作PM的垂线交PM于点M,则OM的长度为().秒杀类型5秒杀结论⑨FG=FE=FH=a练习1.(太原二模)已知双曲线的左右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是().秒杀类型5练习2.(银川一中三模)设P是双曲线上除顶点外的任意一点,F1,F2分别是双曲线的左、右焦点,△PF1F2的内切圆与边F1F2相切于点M,则F1M·MF2=().A.5 B.4 C.2 D.1秒杀类型5
同课章节目录
