29.2 第3课时 几何体的表面展开图 同步课时作业(含答案)
文档属性
| 名称 | 29.2 第3课时 几何体的表面展开图 同步课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 08:02:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十九章 投影与视图
29.2 三视图
第3课时 几何体的表面展开图
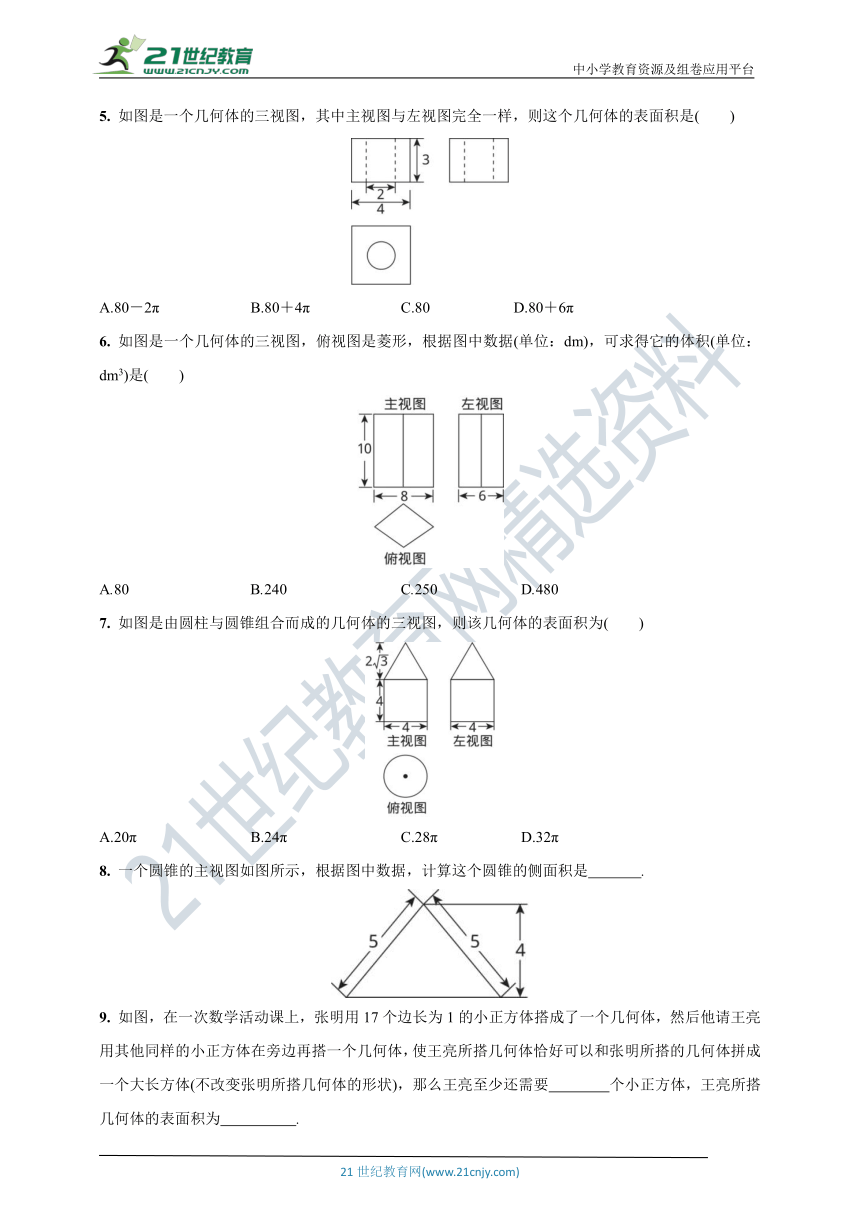
1. 如图是一个几何体的三视图,则该几何体的展开图是( )
2. 如图是一个几何体的展开图,下列哪一个平面图形不是它的三视图中的一个视图( )
3. 一个几何体的主视图、左视图、俯视图都是大小相同的正方形,下列四个选项不是该几何体的表面展开图的是( )
4. 某长方体的主视图与左视图如图所示,则这个长方体的表面积是( )
A.27 cm2 B.54 cm2 C.94 cm2 D.120 cm2
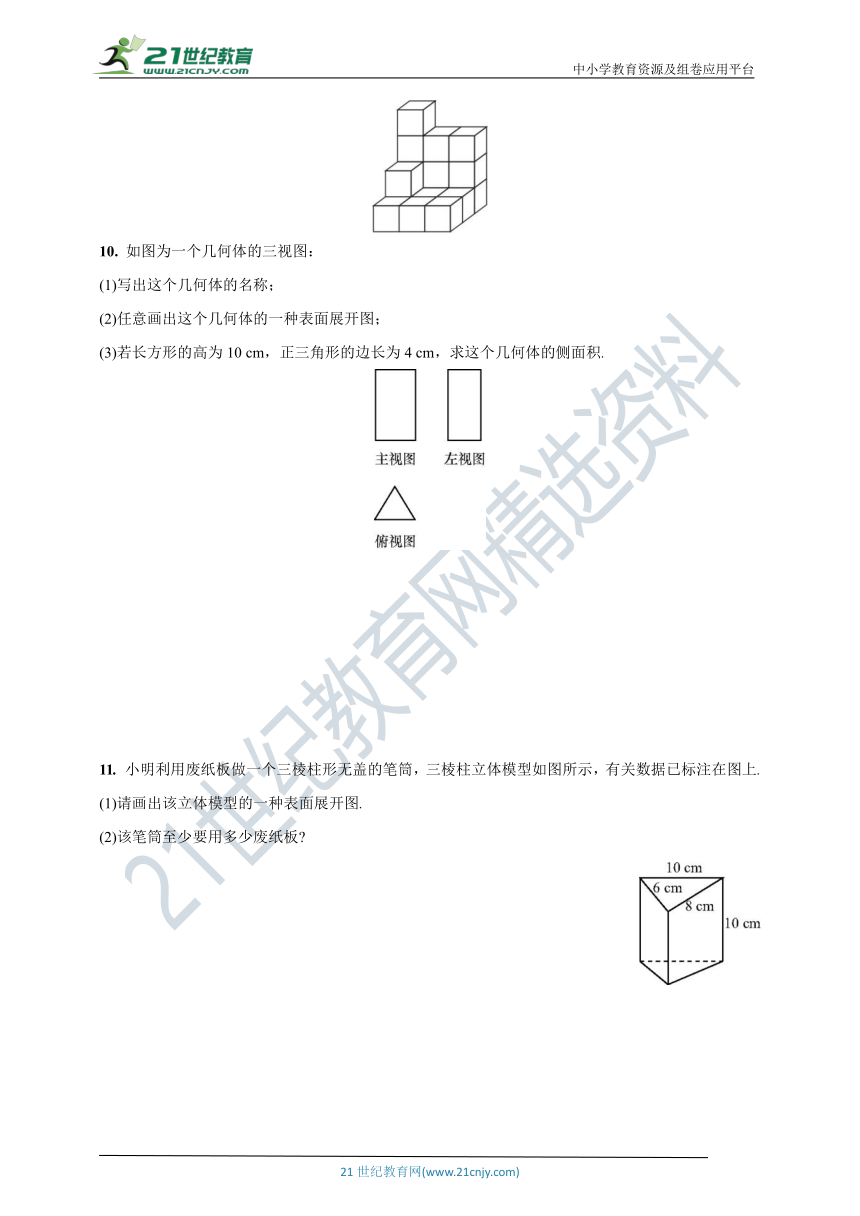
5. 如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A.80-2π B.80+4π C.80 D.80+6π
6. 如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:dm),可求得它的体积(单位:dm3)是( )
A.80 B.240 C.250 D.480
7. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
8. 一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是 .
9. 如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小正方体,王亮所搭几何体的表面积为 .
10. 如图为一个几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10 cm,正三角形的边长为4 cm,求这个几何体的侧面积.
11. 小明利用废纸板做一个三棱柱形无盖的笔筒,三棱柱立体模型如图所示,有关数据已标注在图上.
(1)请画出该立体模型的一种表面展开图.
(2)该笔筒至少要用多少废纸板
12. 一个几何体的三视图如图所示,分别求出这个几何体的体积和表面积.
13. 如图是由两个长方体组合而成的一个立体图形的主视图和左视图,根据图中所标尺寸(单位:mm).
(1)直接写出上下两个长方体的长、宽、高分别是多少;
(2)求这个立体图形的体积.
参 考 答 案
1. B 2. D 3. C 4. C 5. B 6. B 7. C
8. 15π
9. 19 48
10. 解:(1)这个几何体是正三棱柱.
(2)图略.
(3)侧面积为3×10×4=120(cm2).
11. 解:(1)图略.
(2)∵62+82=102,∴底面三角形为直角三角形,(6+8+10)×10+×6×8=240+24=264 cm2.
答:该笔筒至少要用264 cm2的废纸板.
12. 解:体积为3×1×3+3×3×1=9+9=18,表面积为(3×3+1×3)×2+(3×3+3×1+3×1)×2=54.
13. 解:(1)根据三视图可得上面的长方体长4 mm,宽2 mm,高4 mm,下面的长方体长6 mm,宽8 mm,高2 mm.
(2)立体图形的体积是4×2×4+6×8×2=128(mm3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十九章 投影与视图
29.2 三视图
第3课时 几何体的表面展开图
1. 如图是一个几何体的三视图,则该几何体的展开图是( )
2. 如图是一个几何体的展开图,下列哪一个平面图形不是它的三视图中的一个视图( )
3. 一个几何体的主视图、左视图、俯视图都是大小相同的正方形,下列四个选项不是该几何体的表面展开图的是( )
4. 某长方体的主视图与左视图如图所示,则这个长方体的表面积是( )
A.27 cm2 B.54 cm2 C.94 cm2 D.120 cm2
5. 如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A.80-2π B.80+4π C.80 D.80+6π
6. 如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:dm),可求得它的体积(单位:dm3)是( )
A.80 B.240 C.250 D.480
7. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
8. 一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是 .
9. 如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小正方体,王亮所搭几何体的表面积为 .
10. 如图为一个几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10 cm,正三角形的边长为4 cm,求这个几何体的侧面积.
11. 小明利用废纸板做一个三棱柱形无盖的笔筒,三棱柱立体模型如图所示,有关数据已标注在图上.
(1)请画出该立体模型的一种表面展开图.
(2)该笔筒至少要用多少废纸板
12. 一个几何体的三视图如图所示,分别求出这个几何体的体积和表面积.
13. 如图是由两个长方体组合而成的一个立体图形的主视图和左视图,根据图中所标尺寸(单位:mm).
(1)直接写出上下两个长方体的长、宽、高分别是多少;
(2)求这个立体图形的体积.
参 考 答 案
1. B 2. D 3. C 4. C 5. B 6. B 7. C
8. 15π
9. 19 48
10. 解:(1)这个几何体是正三棱柱.
(2)图略.
(3)侧面积为3×10×4=120(cm2).
11. 解:(1)图略.
(2)∵62+82=102,∴底面三角形为直角三角形,(6+8+10)×10+×6×8=240+24=264 cm2.
答:该笔筒至少要用264 cm2的废纸板.
12. 解:体积为3×1×3+3×3×1=9+9=18,表面积为(3×3+1×3)×2+(3×3+3×1+3×1)×2=54.
13. 解:(1)根据三视图可得上面的长方体长4 mm,宽2 mm,高4 mm,下面的长方体长6 mm,宽8 mm,高2 mm.
(2)立体图形的体积是4×2×4+6×8×2=128(mm3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
