29.3 课题学习 制作立体模型 同步练习(含答案)
文档属性
| 名称 | 29.3 课题学习 制作立体模型 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 08:59:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十九章 投影与视图
29.3 课题学习 制作立体模型
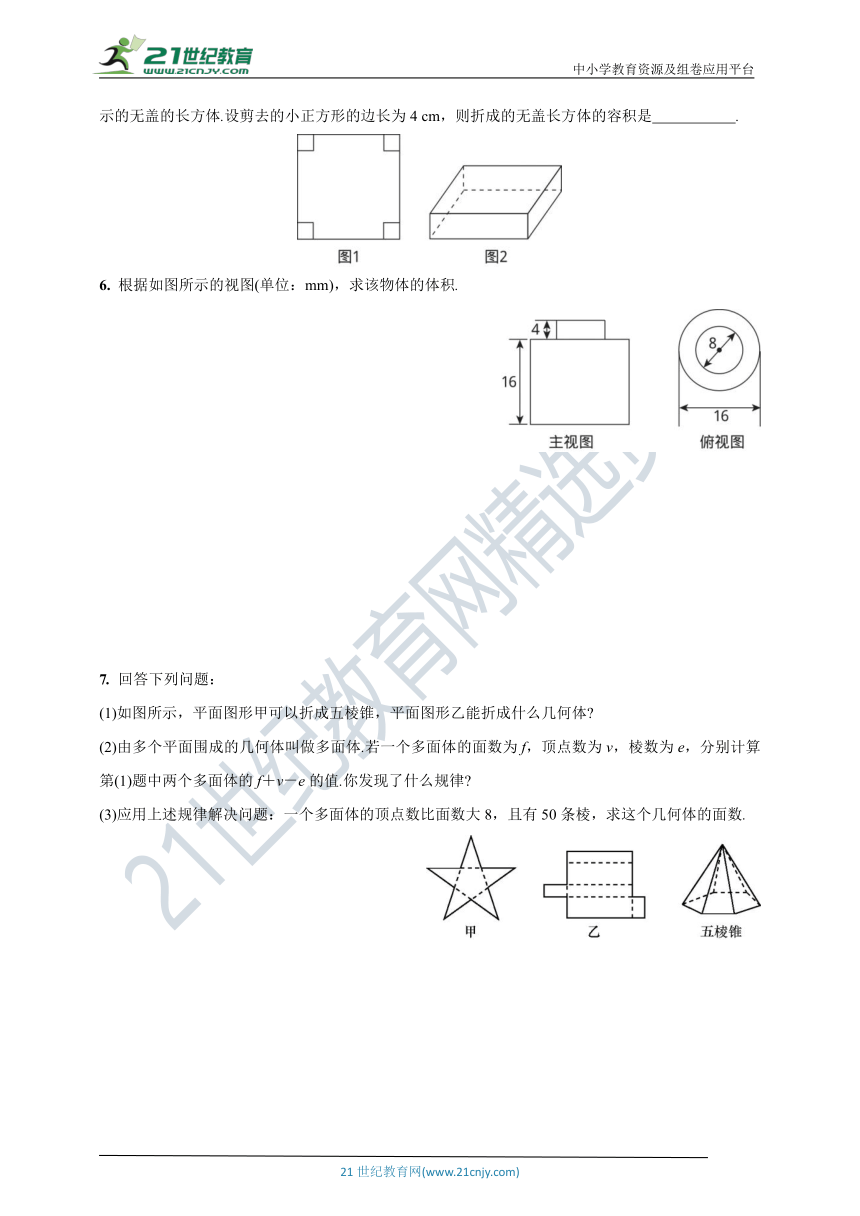
1. 已知某个几何体的主视图和俯视图分别如下,则该几何体可能为( )
2. 如图是某一个多面体的表面展开图,那么这个多面体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
3. 下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是( )
A.①② B.③④ C.② D.③
4. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A B C D
5. 如图1,在边长为18 cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4 cm,则折成的无盖长方体的容积是 .
6. 根据如图所示的视图(单位:mm),求该物体的体积.
7. 回答下列问题:
(1)如图所示,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
参 考 答 案
1. C 2. C 3. C 4. A
5. 400 cm3
6. 解:由三视图知该几何体是两个圆柱叠放在一起,上面圆柱的底面直径为8 mm,高为4 mm,下面圆柱的底面直径为16 mm,高为16 mm,故体积为π(16÷2)2×16+π(8÷2)2×4=1088π(mm3).
7. 解:(1)平面图形乙能折成长方体.
(2)甲:f=6,v=6,e=10,f+v-e=2;乙:f=6,v=8,e=12,f+v-e=2.
规律:面数+顶点数-棱数=2.
(3)设这个多面体的面数为x. 由题可得x+x+8-50=2,解得x=22,∴这个几何体的面数为22.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十九章 投影与视图
29.3 课题学习 制作立体模型
1. 已知某个几何体的主视图和俯视图分别如下,则该几何体可能为( )
2. 如图是某一个多面体的表面展开图,那么这个多面体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
3. 下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是( )
A.①② B.③④ C.② D.③
4. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A B C D
5. 如图1,在边长为18 cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4 cm,则折成的无盖长方体的容积是 .
6. 根据如图所示的视图(单位:mm),求该物体的体积.
7. 回答下列问题:
(1)如图所示,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
参 考 答 案
1. C 2. C 3. C 4. A
5. 400 cm3
6. 解:由三视图知该几何体是两个圆柱叠放在一起,上面圆柱的底面直径为8 mm,高为4 mm,下面圆柱的底面直径为16 mm,高为16 mm,故体积为π(16÷2)2×16+π(8÷2)2×4=1088π(mm3).
7. 解:(1)平面图形乙能折成长方体.
(2)甲:f=6,v=6,e=10,f+v-e=2;乙:f=6,v=8,e=12,f+v-e=2.
规律:面数+顶点数-棱数=2.
(3)设这个多面体的面数为x. 由题可得x+x+8-50=2,解得x=22,∴这个几何体的面数为22.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
