人教版九年级下册:第二十九章《投影与视图》达标检测卷(含答案)
文档属性
| 名称 | 人教版九年级下册:第二十九章《投影与视图》达标检测卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 07:50:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学第二十九章达标检测卷
【检测内容:第二十九章 投影与视图 满分:120分】
一、选择题(每小题3分,共30分)
1. 下面四个几何体中,主视图为三角形的是( )
A B C D
2. 如图所示的几何体,它的俯视图是( )
3. 如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
A.越小 B.越大 C.不变 D.无法确定
4. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
5. 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
6. 如图是用八块完全相同的小正方体搭成的几何体,其左视图是( )
7. 如图是某圆锥的主视图和左视图,则该圆锥的全面积是( )
A.36π B.24π C.20π D.15π
8. 某个几何体是由七个相同的小正方体组成,若它的俯视图如图所示,则它的主视图不可能是( )
9. 如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
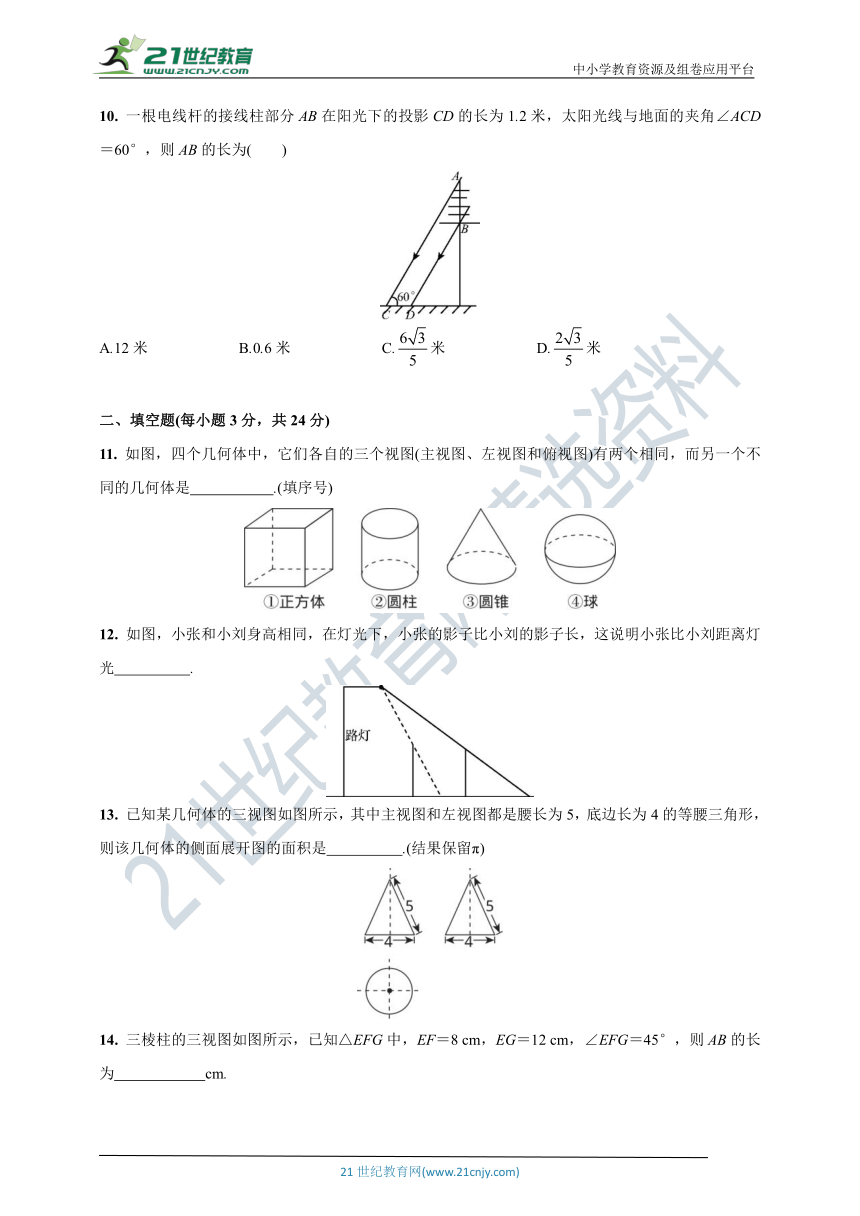
10. 一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
A.12米 B.0.6米 C.米 D.米
二、填空题(每小题3分,共24分)
11. 如图,四个几何体中,它们各自的三个视图(主视图、左视图和俯视图)有两个相同,而另一个不同的几何体是 .(填序号)
12. 如图,小张和小刘身高相同,在灯光下,小张的影子比小刘的影子长,这说明小张比小刘距离灯光 .
13. 已知某几何体的三视图如图所示,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 .(结果保留π)
14. 三棱柱的三视图如图所示,已知△EFG中,EF=8 cm,EG=12 cm,∠EFG=45°,则AB的长为 cm.
15. 在平面直角坐标系内,一点光源位于A(0,5)处,线段CD垂直于x轴,D为垂足,C(3,1),则点C的影子E的坐标为 .
16. 用八个同样大小的小立方体粘成一个大立方体如图1,得到的几何体的三视图如图2所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图2,则他取走的小立方体最多可以是 个.
17. 小芳的房间有一个面积为3 m2的玻璃窗,她站在室内离窗子4 m的地方向外看,她能看到窗前面一幢楼房的面积有 m2.(楼之间的距离为20 m)
18. 有一个棱长为5的正方体木块,从它的每一个面看都有一个穿透的完全相同的孔(如图中的阴影部分),则这个立体图形的内、外表面的总面积是 .
三、解答题(共66分)
19.(8分)如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)图2是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图.
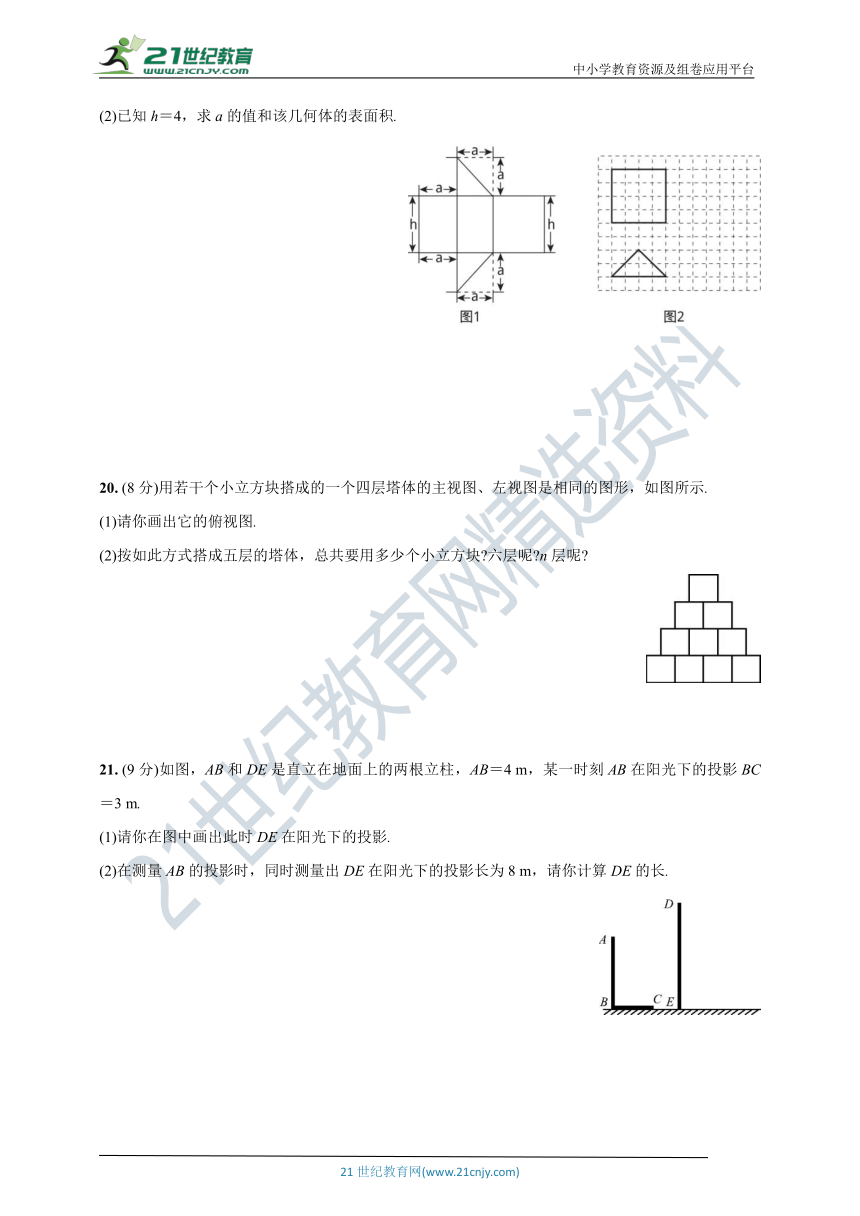
(2)已知h=4,求a的值和该几何体的表面积.
20. (8分)用若干个小立方块搭成的一个四层塔体的主视图、左视图是相同的图形,如图所示.
(1)请你画出它的俯视图.
(2)按如此方式搭成五层的塔体,总共要用多少个小立方块 六层呢 n层呢
21. (9分)如图,AB和DE是直立在地面上的两根立柱,AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
22. (9分)如图是某工件的三视图,求此工件的全面积和体积.
23. (10分)如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
24. (10分)如图是住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=30 m,现需要了解甲楼对乙楼采光的影响情况.
(1)当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高;(结果精确到0.1 m,取1.73)
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳光与水平线的夹角为多少度
25. (12分)小明在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置 请你帮助小明在①上补全.
(3)已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
参 考 答 案
1. B 2. D 3. B 4. D 5. C 6. A 7. A 8. D 9. B 10. C
11. ②③
12. 远
13. 10π
14. 4
15. (,0)
16. 4
17. 108
18. 216
19. 解:(1)如图所示.
(2)根据俯视图和主视图可知a2+a2=h2=42,解得a=2.几何体的表面积为2ah+ah+a2×2=16+24.
20. 解:(1)如图所示.
(2)按如此方式搭成五层的塔体,总共要用12+22+…+52=55个小立方块;六层的塔体,总共要用12+22+…+62=91个小立方块;n层的塔体,总共要用(12+22+…+n2)个小立方块.
21. 解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE在阳光下的投影.
(2)由(1)知AC∥DF,∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF,∴AB∶DE=BC∶EF,即4∶DE=3∶8,解得DE= m.
22. 解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体,这圆锥的母线长为=10(cm),圆锥的侧面积为s=πrl=×20π×10=100π(cm2),圆锥的底面积为102π=100π(cm2),圆锥的全面积为100π+100π=100(1+)π(cm2),圆锥的体积为×π×(20÷2)2×30=1000 π(cm3).故此工件的全面积是100(1+)π cm2,体积是1000π cm3.
23. 解:连接CD.由题易知∠B=90°,∠DOE=90°,点O,D,C共线.∵OD=0.8 m,OE=0.8 m,∴∠DEB=45°.∵∠B=90°,∴∠BAE=45°,∴AB=BE,设AB=EB=x m.∵∠B=∠DOE=90°,∴AB∥CO,∴△ABF∽△COF,∴=,即=,解得x=4.4.经检验x=4.4是原方程的解.答:围墙AB的高度是4.4 m.
24. 解:(1)如图,延长OB交DC于点E,过点E作EF⊥AB,交AB于点F.在Rt△BFE中,EF=AC=30 m,∠FEB=30°,∴BF=EF·tan 30°≈17.3 m,EC=30-17.3=12.7 m.答:甲楼的影子在乙楼上有12.7 m高.
(2)当甲楼的影子刚好落在点C处时,△ABC为等腰直角三角形,∴当太阳光与水平线的夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.
25. 解:(1)8
(2)如图所示.(答案不唯一)
(3)∵长方体纸盒的底面是一个正方形,∴可设底面边长为a cm.∵长方体纸盒所有棱长的和是880 cm,长方体纸盒高为20 cm,∴4×20+8a=880,解得a=100,∴这个长方体纸盒的体积为20×100×100=200000(cm3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学第二十九章达标检测卷
【检测内容:第二十九章 投影与视图 满分:120分】
一、选择题(每小题3分,共30分)
1. 下面四个几何体中,主视图为三角形的是( )
A B C D
2. 如图所示的几何体,它的俯视图是( )
3. 如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
A.越小 B.越大 C.不变 D.无法确定
4. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
5. 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
6. 如图是用八块完全相同的小正方体搭成的几何体,其左视图是( )
7. 如图是某圆锥的主视图和左视图,则该圆锥的全面积是( )
A.36π B.24π C.20π D.15π
8. 某个几何体是由七个相同的小正方体组成,若它的俯视图如图所示,则它的主视图不可能是( )
9. 如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
10. 一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
A.12米 B.0.6米 C.米 D.米
二、填空题(每小题3分,共24分)
11. 如图,四个几何体中,它们各自的三个视图(主视图、左视图和俯视图)有两个相同,而另一个不同的几何体是 .(填序号)
12. 如图,小张和小刘身高相同,在灯光下,小张的影子比小刘的影子长,这说明小张比小刘距离灯光 .
13. 已知某几何体的三视图如图所示,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 .(结果保留π)
14. 三棱柱的三视图如图所示,已知△EFG中,EF=8 cm,EG=12 cm,∠EFG=45°,则AB的长为 cm.
15. 在平面直角坐标系内,一点光源位于A(0,5)处,线段CD垂直于x轴,D为垂足,C(3,1),则点C的影子E的坐标为 .
16. 用八个同样大小的小立方体粘成一个大立方体如图1,得到的几何体的三视图如图2所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图2,则他取走的小立方体最多可以是 个.
17. 小芳的房间有一个面积为3 m2的玻璃窗,她站在室内离窗子4 m的地方向外看,她能看到窗前面一幢楼房的面积有 m2.(楼之间的距离为20 m)
18. 有一个棱长为5的正方体木块,从它的每一个面看都有一个穿透的完全相同的孔(如图中的阴影部分),则这个立体图形的内、外表面的总面积是 .
三、解答题(共66分)
19.(8分)如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)图2是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图.
(2)已知h=4,求a的值和该几何体的表面积.
20. (8分)用若干个小立方块搭成的一个四层塔体的主视图、左视图是相同的图形,如图所示.
(1)请你画出它的俯视图.
(2)按如此方式搭成五层的塔体,总共要用多少个小立方块 六层呢 n层呢
21. (9分)如图,AB和DE是直立在地面上的两根立柱,AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
22. (9分)如图是某工件的三视图,求此工件的全面积和体积.
23. (10分)如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
24. (10分)如图是住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=30 m,现需要了解甲楼对乙楼采光的影响情况.
(1)当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高;(结果精确到0.1 m,取1.73)
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳光与水平线的夹角为多少度
25. (12分)小明在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置 请你帮助小明在①上补全.
(3)已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
参 考 答 案
1. B 2. D 3. B 4. D 5. C 6. A 7. A 8. D 9. B 10. C
11. ②③
12. 远
13. 10π
14. 4
15. (,0)
16. 4
17. 108
18. 216
19. 解:(1)如图所示.
(2)根据俯视图和主视图可知a2+a2=h2=42,解得a=2.几何体的表面积为2ah+ah+a2×2=16+24.
20. 解:(1)如图所示.
(2)按如此方式搭成五层的塔体,总共要用12+22+…+52=55个小立方块;六层的塔体,总共要用12+22+…+62=91个小立方块;n层的塔体,总共要用(12+22+…+n2)个小立方块.
21. 解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE在阳光下的投影.
(2)由(1)知AC∥DF,∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF,∴AB∶DE=BC∶EF,即4∶DE=3∶8,解得DE= m.
22. 解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体,这圆锥的母线长为=10(cm),圆锥的侧面积为s=πrl=×20π×10=100π(cm2),圆锥的底面积为102π=100π(cm2),圆锥的全面积为100π+100π=100(1+)π(cm2),圆锥的体积为×π×(20÷2)2×30=1000 π(cm3).故此工件的全面积是100(1+)π cm2,体积是1000π cm3.
23. 解:连接CD.由题易知∠B=90°,∠DOE=90°,点O,D,C共线.∵OD=0.8 m,OE=0.8 m,∴∠DEB=45°.∵∠B=90°,∴∠BAE=45°,∴AB=BE,设AB=EB=x m.∵∠B=∠DOE=90°,∴AB∥CO,∴△ABF∽△COF,∴=,即=,解得x=4.4.经检验x=4.4是原方程的解.答:围墙AB的高度是4.4 m.
24. 解:(1)如图,延长OB交DC于点E,过点E作EF⊥AB,交AB于点F.在Rt△BFE中,EF=AC=30 m,∠FEB=30°,∴BF=EF·tan 30°≈17.3 m,EC=30-17.3=12.7 m.答:甲楼的影子在乙楼上有12.7 m高.
(2)当甲楼的影子刚好落在点C处时,△ABC为等腰直角三角形,∴当太阳光与水平线的夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.
25. 解:(1)8
(2)如图所示.(答案不唯一)
(3)∵长方体纸盒的底面是一个正方形,∴可设底面边长为a cm.∵长方体纸盒所有棱长的和是880 cm,长方体纸盒高为20 cm,∴4×20+8a=880,解得a=100,∴这个长方体纸盒的体积为20×100×100=200000(cm3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
