第七章 相交线与平行线 章末复习(含答案)
文档属性
| 名称 | 第七章 相交线与平行线 章末复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-06 23:13:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
章末复习
考点突破
考点一 相交线及有关概念
1.如图,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°31′,则下列结论不正确的是( )
A.∠AOD与∠1互为补角 B.∠1=∠3 C.∠1的余角等于75°29′ D.∠2=45°
2.如图,河道的同侧有M,N两个村庄,计划铺设一条管道将河水引至M,N两地,下列四个方案中,管道长度最短的是( )
3.∠α的补角是它的3倍,则∠α的余角的度数是_________.
4.如图,直线AB,CD,EF相交于点O,且AB⊥EF,OG平分∠AOD.若∠BOC=70°,则∠GOF的度数是______.
5.如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=110°,求∠BOD的度数.
考点二 平行线的判定与性质
6.如图,下列推理及说明的理由都正确的是( )
A.若AB∥DG,则∠BAC=∠DCA,理由是内错角相等,两直线平行
B.若AB∥DG,则∠1=∠2,理由是两直线平行,内错角相等
C.若AE∥CF,则∠E=∠F,理由是内错角相等,两直线平行
D.若AE∥CF,则∠1=∠2,理由是两直线平行,内错角相等
第6题图 第7题图
7.如图,CD⊥AB,EF⊥AB,垂足分别为D,F,下列条件不能推出∠ADG=∠B的是( )
A.∠1=2 B.∠1=∠3 C.∠2=∠3 D.∠DGC+∠ACB=180°
8.如图,直线AB∥CD,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分∠CEF,则∠1的度数为__________.
第8题图 第9题图
9.如图,∠1=∠2=40°,MN平分∠EMB,则∠3=__________.
10.如图,直线EF分别与直线AB,CD交于点E,F,EM平分∠BEF,FN平分∠CFE,且EM∥FN.试说明:AB∥CD.
素养提升
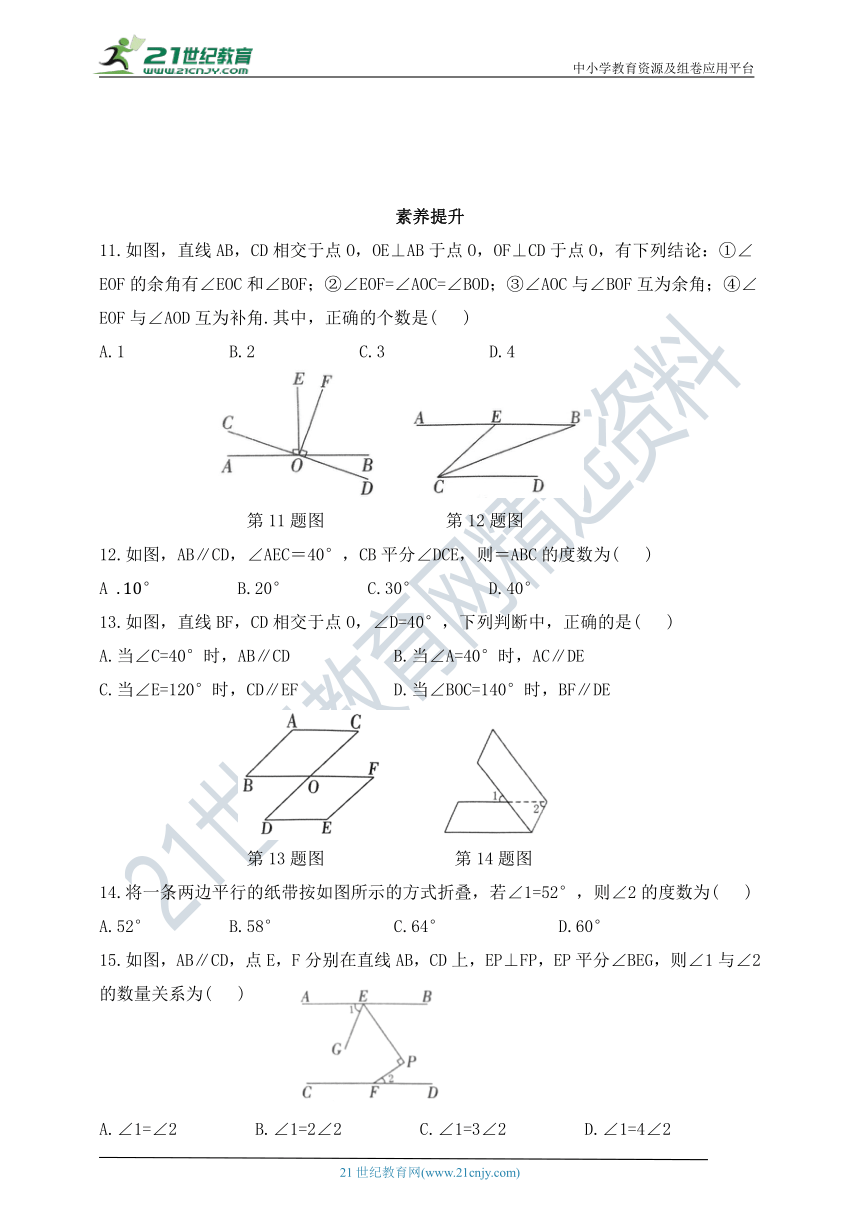
11.如图,直线AB,CD相交于点O,OE⊥AB于点O,OF⊥CD于点O,有下列结论:①∠EOF的余角有∠EOC和∠BOF;②∠EOF=∠AOC=∠BOD;③∠AOC与∠BOF互为余角;④∠EOF与∠AOD互为补角.其中,正确的个数是( )
A.1 B.2 C.3 D.4
第11题图 第12题图
12.如图,AB∥CD,∠AEC=40°,CB平分∠DCE,则=ABC的度数为( )
A ° B.20° C.30° D.40°
13.如图,直线BF,CD相交于点O,∠D=40°,下列判断中,正确的是( )
A.当∠C=40°时,AB∥CD B.当∠A=40°时,AC∥DE
C.当∠E=120°时,CD∥EF D.当∠BOC=140°时,BF∥DE
第13题图 第14题图
14.将一条两边平行的纸带按如图所示的方式折叠,若∠1=52°,则∠2的度数为( )
A.52° B.58° C.64° D.60°
15.如图,AB∥CD,点E,F分别在直线AB,CD上,EP⊥FP,EP平分∠BEG,则∠1与∠2的数量关系为( )
A.∠1=∠2 B.∠1=2∠2 C.∠1=3∠2 D.∠1=4∠2
16.如图,因为直线AB⊥于点B,BC⊥于点B,所以直线AB和BC重合,则其中蕴含的数学原理是____________________________________________________.
17.一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为_________.
第17题图 第18题图
18.某段江水流向经过B,C,D三点拐弯后与原来流向相同.如图,若∠B=120°,∠C=80°,则∠D=_________.
19.已知一个角为50°,另一个角的两边分别与该角的两边互相平行,则另一个角的度数为__________.
20.如图,利用尺规在三角形ABC的边AC上方作∠CAD=∠ACB(尺规作图,不写作法,保留作图痕迹).
21.如图,∠COE与∠EOD互余,OE平分∠AOD,∠AOB=140°.
(1)若∠COE=40°,则∠DOE=__________,∠BOD=_________;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
22.如图,AB∥CD,∠B=120°,EF是∠BEC的平分线,FG∥HD,求∠D的度数.
23.如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥BD,垂足为B,EG平分∠DEB,
∠CDE=50°,∠F=25°.
(1)试说明:EG⊥BD;
(2)求∠CDB的度数.
24.(1)如图①,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.请判断AB与CD的位置关系,并说明理由.
(2)如图②,若∠E=90°,且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=
∠ECD.在直角顶点E移动的过程中,∠BAE与∠MCD是否存在确定的数量关系 请说明理由.
(3)如图③,P为线段AC上一定点,Q为直线CD上一动点,且AB与CD的位置关系保持不变.当点Q在射线CD上运动时(不与点C重合),∠PQC+∠QPC与∠BAC有何数量关系?请说明理由.
参考答案
[考点突破]
1.C 2.A 3.45° 4.55°
5.(1)与∠AOD互补的角:∠BOD,∠AOC,∠DOE (2)因为∠AOE=110°,所以∠BOE=180°-∠AOE=180°-110°=70°.因为OF平分∠AOE,所以
110°=55°.因为OF⊥CD,所以∠FOD=90°.所以∠EOD=∠FOD-∠FOE=90°-55°=35°.所以∠BOD=∠BOE-∠EOD=70°-35°=35°.
6.D 7.C 8.60° 9.110°
10.因为EM∥FN,所以∠FEM=∠EFN.因为EM平分∠BEF,FN平分∠CFE,所以∠BEF=2∠FEM,∠CFE=2∠EFN.所以∠BEF=∠CFE.所以AB∥CD .
[素养提升]
11.D 12.B 13.D 14.C 15.B 16.平面内,过一点有且只有一条直线与已知直线垂直 17.270° 18.20° 19.50°或130°
20.如图,∠CAD即为所求作
21.(1)50° 40° 解析:因为∠COE与∠EOD互余,∠COE=40°,所以∠DOE=90°-40°=50°.因为OE平分∠AOD,所以∠AOD=2∠DOE=100°.所以∠BOD=∠AOB-∠AOD=40°.
(2)因为∠COE=α,且∠COE与∠EOD互余,所以∠EOD=90°-α.因为OE平分∠AOD,所
以∠AOD=2(90°-a).所以∠β2(90°-α)=2α-40°.
22.因为AB∥CD,所以∠BEC+∠B=180°.所以∠BEC=180°-∠
因为EF是∠BEC的平分线,所以 因为FG∥HD,所以
∠D=∠CEF=30°.
23.(1)因为AB∥CD,∠CDE=50°,所以∠DEB=∠CDE=50°.因为EG平分∠DEB,所以∠DEG=∠BEG=∠DEB=25°,因为∠F=25°,所以∠DEG=∠F.所以BF∥EG.因为FB⊥BD,所以∠FBD=90°.所以∠EGD=∠FBD=90°.所以EG⊥BD.
(2)由(1),得∠FBD=90°.因为BF∥EG,所以∠EBF=∠BEG=25°.所以∠EBG=∠FBD-∠EBF=65°.因为AB∥CD,所以∠EBG+∠CDB=180°.所以∠CDB= 180°-65°=115°.
24.(1)AB∥CD 理由:因为CE平分∠ACD,AE平分∠BAC,所以∠BAC=2∠EAC,∠ACD=2∠ACE.因为∠EAC+∠ACE=90°,所以∠BAC+∠ACD=2(∠EAC+∠ACE)=2×90°=180°.所以AB∥CD.
(2)存在, 理由:过点E向右作EF∥AB.因为AB∥CD,所以EF∥AB∥CD.所以∠BAE=∠AEF,∠FEC=∠ECD.因为∠AEC=90°,所以∠AEF+∠FEC=90°.所以∠BAE+∠ECD=90°.因为∠MCE=∠ECD,即∠MCD,所以∠MCD=90°.
(3)∠BAC=∠PQC+∠QPC 理由:过点P向左作PR∥AB.因为AB∥CD,所以PR∥AB∥CD.所以∠BAC=∠RPC,∠RPQ=∠PQC.因为∠RPC=∠RPQ+∠QPC,所以∠BAC=∠PQC+∠QPC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
章末复习
考点突破
考点一 相交线及有关概念
1.如图,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°31′,则下列结论不正确的是( )
A.∠AOD与∠1互为补角 B.∠1=∠3 C.∠1的余角等于75°29′ D.∠2=45°
2.如图,河道的同侧有M,N两个村庄,计划铺设一条管道将河水引至M,N两地,下列四个方案中,管道长度最短的是( )
3.∠α的补角是它的3倍,则∠α的余角的度数是_________.
4.如图,直线AB,CD,EF相交于点O,且AB⊥EF,OG平分∠AOD.若∠BOC=70°,则∠GOF的度数是______.
5.如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=110°,求∠BOD的度数.
考点二 平行线的判定与性质
6.如图,下列推理及说明的理由都正确的是( )
A.若AB∥DG,则∠BAC=∠DCA,理由是内错角相等,两直线平行
B.若AB∥DG,则∠1=∠2,理由是两直线平行,内错角相等
C.若AE∥CF,则∠E=∠F,理由是内错角相等,两直线平行
D.若AE∥CF,则∠1=∠2,理由是两直线平行,内错角相等
第6题图 第7题图
7.如图,CD⊥AB,EF⊥AB,垂足分别为D,F,下列条件不能推出∠ADG=∠B的是( )
A.∠1=2 B.∠1=∠3 C.∠2=∠3 D.∠DGC+∠ACB=180°
8.如图,直线AB∥CD,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分∠CEF,则∠1的度数为__________.
第8题图 第9题图
9.如图,∠1=∠2=40°,MN平分∠EMB,则∠3=__________.
10.如图,直线EF分别与直线AB,CD交于点E,F,EM平分∠BEF,FN平分∠CFE,且EM∥FN.试说明:AB∥CD.
素养提升
11.如图,直线AB,CD相交于点O,OE⊥AB于点O,OF⊥CD于点O,有下列结论:①∠EOF的余角有∠EOC和∠BOF;②∠EOF=∠AOC=∠BOD;③∠AOC与∠BOF互为余角;④∠EOF与∠AOD互为补角.其中,正确的个数是( )
A.1 B.2 C.3 D.4
第11题图 第12题图
12.如图,AB∥CD,∠AEC=40°,CB平分∠DCE,则=ABC的度数为( )
A ° B.20° C.30° D.40°
13.如图,直线BF,CD相交于点O,∠D=40°,下列判断中,正确的是( )
A.当∠C=40°时,AB∥CD B.当∠A=40°时,AC∥DE
C.当∠E=120°时,CD∥EF D.当∠BOC=140°时,BF∥DE
第13题图 第14题图
14.将一条两边平行的纸带按如图所示的方式折叠,若∠1=52°,则∠2的度数为( )
A.52° B.58° C.64° D.60°
15.如图,AB∥CD,点E,F分别在直线AB,CD上,EP⊥FP,EP平分∠BEG,则∠1与∠2的数量关系为( )
A.∠1=∠2 B.∠1=2∠2 C.∠1=3∠2 D.∠1=4∠2
16.如图,因为直线AB⊥于点B,BC⊥于点B,所以直线AB和BC重合,则其中蕴含的数学原理是____________________________________________________.
17.一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为_________.
第17题图 第18题图
18.某段江水流向经过B,C,D三点拐弯后与原来流向相同.如图,若∠B=120°,∠C=80°,则∠D=_________.
19.已知一个角为50°,另一个角的两边分别与该角的两边互相平行,则另一个角的度数为__________.
20.如图,利用尺规在三角形ABC的边AC上方作∠CAD=∠ACB(尺规作图,不写作法,保留作图痕迹).
21.如图,∠COE与∠EOD互余,OE平分∠AOD,∠AOB=140°.
(1)若∠COE=40°,则∠DOE=__________,∠BOD=_________;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
22.如图,AB∥CD,∠B=120°,EF是∠BEC的平分线,FG∥HD,求∠D的度数.
23.如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥BD,垂足为B,EG平分∠DEB,
∠CDE=50°,∠F=25°.
(1)试说明:EG⊥BD;
(2)求∠CDB的度数.
24.(1)如图①,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.请判断AB与CD的位置关系,并说明理由.
(2)如图②,若∠E=90°,且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=
∠ECD.在直角顶点E移动的过程中,∠BAE与∠MCD是否存在确定的数量关系 请说明理由.
(3)如图③,P为线段AC上一定点,Q为直线CD上一动点,且AB与CD的位置关系保持不变.当点Q在射线CD上运动时(不与点C重合),∠PQC+∠QPC与∠BAC有何数量关系?请说明理由.
参考答案
[考点突破]
1.C 2.A 3.45° 4.55°
5.(1)与∠AOD互补的角:∠BOD,∠AOC,∠DOE (2)因为∠AOE=110°,所以∠BOE=180°-∠AOE=180°-110°=70°.因为OF平分∠AOE,所以
110°=55°.因为OF⊥CD,所以∠FOD=90°.所以∠EOD=∠FOD-∠FOE=90°-55°=35°.所以∠BOD=∠BOE-∠EOD=70°-35°=35°.
6.D 7.C 8.60° 9.110°
10.因为EM∥FN,所以∠FEM=∠EFN.因为EM平分∠BEF,FN平分∠CFE,所以∠BEF=2∠FEM,∠CFE=2∠EFN.所以∠BEF=∠CFE.所以AB∥CD .
[素养提升]
11.D 12.B 13.D 14.C 15.B 16.平面内,过一点有且只有一条直线与已知直线垂直 17.270° 18.20° 19.50°或130°
20.如图,∠CAD即为所求作
21.(1)50° 40° 解析:因为∠COE与∠EOD互余,∠COE=40°,所以∠DOE=90°-40°=50°.因为OE平分∠AOD,所以∠AOD=2∠DOE=100°.所以∠BOD=∠AOB-∠AOD=40°.
(2)因为∠COE=α,且∠COE与∠EOD互余,所以∠EOD=90°-α.因为OE平分∠AOD,所
以∠AOD=2(90°-a).所以∠β2(90°-α)=2α-40°.
22.因为AB∥CD,所以∠BEC+∠B=180°.所以∠BEC=180°-∠
因为EF是∠BEC的平分线,所以 因为FG∥HD,所以
∠D=∠CEF=30°.
23.(1)因为AB∥CD,∠CDE=50°,所以∠DEB=∠CDE=50°.因为EG平分∠DEB,所以∠DEG=∠BEG=∠DEB=25°,因为∠F=25°,所以∠DEG=∠F.所以BF∥EG.因为FB⊥BD,所以∠FBD=90°.所以∠EGD=∠FBD=90°.所以EG⊥BD.
(2)由(1),得∠FBD=90°.因为BF∥EG,所以∠EBF=∠BEG=25°.所以∠EBG=∠FBD-∠EBF=65°.因为AB∥CD,所以∠EBG+∠CDB=180°.所以∠CDB= 180°-65°=115°.
24.(1)AB∥CD 理由:因为CE平分∠ACD,AE平分∠BAC,所以∠BAC=2∠EAC,∠ACD=2∠ACE.因为∠EAC+∠ACE=90°,所以∠BAC+∠ACD=2(∠EAC+∠ACE)=2×90°=180°.所以AB∥CD.
(2)存在, 理由:过点E向右作EF∥AB.因为AB∥CD,所以EF∥AB∥CD.所以∠BAE=∠AEF,∠FEC=∠ECD.因为∠AEC=90°,所以∠AEF+∠FEC=90°.所以∠BAE+∠ECD=90°.因为∠MCE=∠ECD,即∠MCD,所以∠MCD=90°.
(3)∠BAC=∠PQC+∠QPC 理由:过点P向左作PR∥AB.因为AB∥CD,所以PR∥AB∥CD.所以∠BAC=∠RPC,∠RPQ=∠PQC.因为∠RPC=∠RPQ+∠QPC,所以∠BAC=∠PQC+∠QPC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
