6.3.1 平面向量基本定理 同步检测(Word含答案解析)
文档属性
| 名称 | 6.3.1 平面向量基本定理 同步检测(Word含答案解析) | 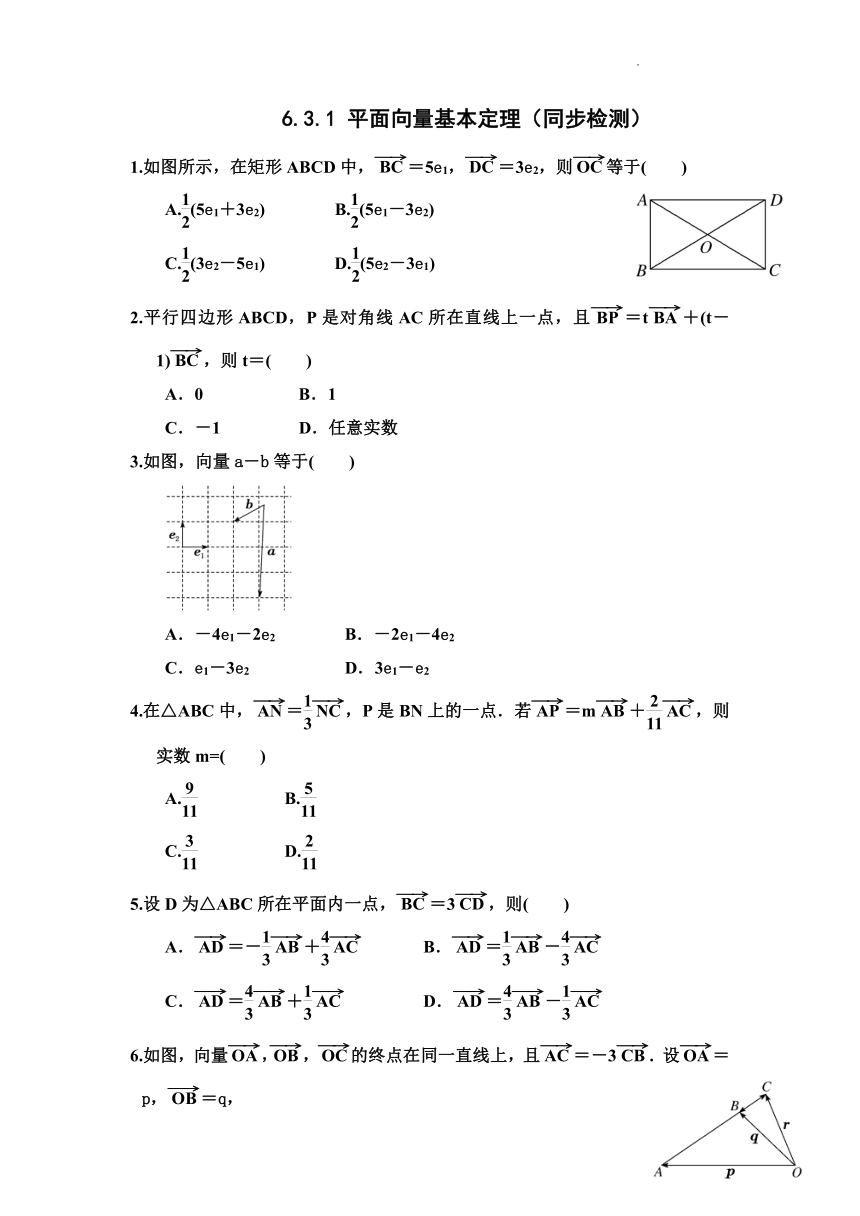 | |
| 格式 | doc | ||
| 文件大小 | 220.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 19:51:52 | ||
图片预览



文档简介
6.3.1 平面向量基本定理(同步检测)
1.如图所示,在矩形ABCD中,=5e1,=3e2,则等于( )
A.(5e1+3e2) B.(5e1-3e2)
C.(3e2-5e1) D.(5e2-3e1)
2.平行四边形ABCD,P是对角线AC所在直线上一点,且=t+(t-1),则t=( )
A.0 B.1
C.-1 D.任意实数
3.如图,向量a-b等于( )
A.-4e1-2e2 B.-2e1-4e2
C.e1-3e2 D.3e1-e2
4.在△ABC中,=,P是BN上的一点.若=m+,则实数m=( )
A. B.
C. D.
5.设D为△ABC所在平面内一点,=3,则( )
A.=-+ B.=-
C.=+ D.=-
6.如图,向量,,的终点在同一直线上,且=-3. 设=p,=q,
=r,则下列等式中成立的是( )
A.r=-p+q B.r=-p+2q
C.r=p-q D.r=-q+2p
7.如图,在△ABC中,点D,E是线段BC上两个动点,且+=x +y,
则+的最小值为 ( )
A. B.2
C. D.
8.(多选)由代数式的乘法法则类比推导向量的数量积的运算法则,正确的选项有( )
A.“mn=nm”类比得到“a·b=b·a”
B.“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”
C.“(mn)t=m(n·t)”类比得到“(a·b)·c=a·(b·c)”
D.“=”类比得到“=”
9.(多选)已知a与b均为单位向量,其夹角为θ,则下列四个结论中正确的是 ( )
A.|a+b|>1 θ∈ B.|a+b|>1 θ∈
C.|a-b|>1 θ∈ D.|a-b|>1 θ∈
10.已知向量e1,e2不共线,实数x,y满足(2x+y)e1+(3x+2y)e2=0,则x+y=________
11.如图,已知E,F分别是矩形ABCD的边BC,CD的中点,EF与AC交于点G,
若=a,=b,用a,b表示=_________
12.若点M是△ABC所在平面内一点,且满足=+,则△ABM与△ABC的面积之比为________
13.如图,在△ABC中,D为BC的中点,E,F为BC的三等分点.若=a,=b,用a,b表示,,.
14.在梯形ABCD中,∥,M,N分别是DA,BC的中点,且=k.设=e1,
=e2,以e1,e2为基底表示向量,, .
15.设e1,e2是不共线的非零向量,且a=e1-2e2,b=e1+3e2.
(1)求证:{a,b}可以作为一个基底;
(2)以{a,b}为基底,求向量c=3e1-e2的分解式;
(3)若4e1-3e2=λa+μb,求λ,μ的值.
参考答案:
1.A
解析:==(-)=(+)=(5e1+3e2).
2.B
解析:因为,,共始点,且P,A,C三点共线,所以t+t-1=1,故t=1,故选B.
3.C
解析:不妨令a=,b=,则a-b=-=,由平行四边形法则可知=e1-3e2.
4C
解析:设=λ,则=+=+λ=+λ(-)=+λ=(1-λ)+=m+,∴解得
5.A
解析:由题意得=+=+=+-=-+.
6.A
解析:∵=-3,∴=-2=2.
∴r==++=++=+(-)=-=-p+q.
7.D
解析:设=m+n,=λ+μ.
∵B,D,E,C共线,∴m+n=1,λ+μ=1.
∵+=x+y,则x+y=2,
∴+=(x+y)=≥=,当且仅当=,即x=,y=时取等号,
∴+的最小值为.
8.AB
解析:对于A,“a·b=b·a”是向量的数量积的交换律,根据向量数量积的定义可知是正确的;对于B,“(a+b)·c=a·c+b·c”是向量数量积对于加法的分配律,这是正确的;对于C,“(a·b)·c=a·(b·c)”这是错误的,左边是与向量c共线的向量,右边是与向量a共线的向量,其中a·b,b·c都是实数;对于D,“=”这是错误的,等号右边的向量的除法是无意义的,向量没有除法的概念.
9.AD
解析:因为|a+b|>1,则|a|2+2a·b+|b|2>1,可得a·b>-,即|a||b|cos θ=cos θ>-,所以θ∈,故A正确,B错误.因为|a-b|>1,即|a|2-2a·b+|b|2>1,可知a·b<,即|a||b|·cos θ=cos θ<,所以θ∈,故D正确,C错误.
10.答案:0
解析:∵e1,e2不共线,∴解得∴x+y=0.
11.答案:a+b
解析:=-=+-=a+b-=a+b-×=a+b-(a-b)=a+b.
12.答案:1∶4
解析:如图,由=+可知M,B,C三点共线,令=λ ,则
=+=+λ=+λ(-)=(1-λ)+λ λ=,
所以=,即面积之比为1∶4.
13.解:=+=+=a+(b-a)=a+b;
=+=+=a+(b-a)=a+b;=+=+=a+(b-a)
=a+b.
14.解:如图所示,∵=e2,且=k,∴=k=ke2.
又∵+++=0,
∴=---=-++=e1+(k-1)e2.
又∵+++=0,且=-,=,
∴=---=-++=e2.
15.解:(1)证明:若a,b共线,则存在λ∈R,使a=λb,则e1-2e2=λ(e1+3e2).
由e1,e2不共线,得
∴λ不存在,故a与b不共线,∴{a,b}可以作为一个基底.
(2)设c=ma+nb(m,n∈R),则3e1-e2=m(e1-2e2)+n(e1+3e2)=(m+n)e1+(-2m+3n)e2.
∴ ∴c=2a+b.
(3)由4e1-3e2=λa+μb,得4e1-3e2=λ(e1-2e2)+μ(e1+3e2)=(λ+μ)e1+(-2λ+3μ)e2.
∴ 故所求λ,μ的值分别为3和1.
1.如图所示,在矩形ABCD中,=5e1,=3e2,则等于( )
A.(5e1+3e2) B.(5e1-3e2)
C.(3e2-5e1) D.(5e2-3e1)
2.平行四边形ABCD,P是对角线AC所在直线上一点,且=t+(t-1),则t=( )
A.0 B.1
C.-1 D.任意实数
3.如图,向量a-b等于( )
A.-4e1-2e2 B.-2e1-4e2
C.e1-3e2 D.3e1-e2
4.在△ABC中,=,P是BN上的一点.若=m+,则实数m=( )
A. B.
C. D.
5.设D为△ABC所在平面内一点,=3,则( )
A.=-+ B.=-
C.=+ D.=-
6.如图,向量,,的终点在同一直线上,且=-3. 设=p,=q,
=r,则下列等式中成立的是( )
A.r=-p+q B.r=-p+2q
C.r=p-q D.r=-q+2p
7.如图,在△ABC中,点D,E是线段BC上两个动点,且+=x +y,
则+的最小值为 ( )
A. B.2
C. D.
8.(多选)由代数式的乘法法则类比推导向量的数量积的运算法则,正确的选项有( )
A.“mn=nm”类比得到“a·b=b·a”
B.“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”
C.“(mn)t=m(n·t)”类比得到“(a·b)·c=a·(b·c)”
D.“=”类比得到“=”
9.(多选)已知a与b均为单位向量,其夹角为θ,则下列四个结论中正确的是 ( )
A.|a+b|>1 θ∈ B.|a+b|>1 θ∈
C.|a-b|>1 θ∈ D.|a-b|>1 θ∈
10.已知向量e1,e2不共线,实数x,y满足(2x+y)e1+(3x+2y)e2=0,则x+y=________
11.如图,已知E,F分别是矩形ABCD的边BC,CD的中点,EF与AC交于点G,
若=a,=b,用a,b表示=_________
12.若点M是△ABC所在平面内一点,且满足=+,则△ABM与△ABC的面积之比为________
13.如图,在△ABC中,D为BC的中点,E,F为BC的三等分点.若=a,=b,用a,b表示,,.
14.在梯形ABCD中,∥,M,N分别是DA,BC的中点,且=k.设=e1,
=e2,以e1,e2为基底表示向量,, .
15.设e1,e2是不共线的非零向量,且a=e1-2e2,b=e1+3e2.
(1)求证:{a,b}可以作为一个基底;
(2)以{a,b}为基底,求向量c=3e1-e2的分解式;
(3)若4e1-3e2=λa+μb,求λ,μ的值.
参考答案:
1.A
解析:==(-)=(+)=(5e1+3e2).
2.B
解析:因为,,共始点,且P,A,C三点共线,所以t+t-1=1,故t=1,故选B.
3.C
解析:不妨令a=,b=,则a-b=-=,由平行四边形法则可知=e1-3e2.
4C
解析:设=λ,则=+=+λ=+λ(-)=+λ=(1-λ)+=m+,∴解得
5.A
解析:由题意得=+=+=+-=-+.
6.A
解析:∵=-3,∴=-2=2.
∴r==++=++=+(-)=-=-p+q.
7.D
解析:设=m+n,=λ+μ.
∵B,D,E,C共线,∴m+n=1,λ+μ=1.
∵+=x+y,则x+y=2,
∴+=(x+y)=≥=,当且仅当=,即x=,y=时取等号,
∴+的最小值为.
8.AB
解析:对于A,“a·b=b·a”是向量的数量积的交换律,根据向量数量积的定义可知是正确的;对于B,“(a+b)·c=a·c+b·c”是向量数量积对于加法的分配律,这是正确的;对于C,“(a·b)·c=a·(b·c)”这是错误的,左边是与向量c共线的向量,右边是与向量a共线的向量,其中a·b,b·c都是实数;对于D,“=”这是错误的,等号右边的向量的除法是无意义的,向量没有除法的概念.
9.AD
解析:因为|a+b|>1,则|a|2+2a·b+|b|2>1,可得a·b>-,即|a||b|cos θ=cos θ>-,所以θ∈,故A正确,B错误.因为|a-b|>1,即|a|2-2a·b+|b|2>1,可知a·b<,即|a||b|·cos θ=cos θ<,所以θ∈,故D正确,C错误.
10.答案:0
解析:∵e1,e2不共线,∴解得∴x+y=0.
11.答案:a+b
解析:=-=+-=a+b-=a+b-×=a+b-(a-b)=a+b.
12.答案:1∶4
解析:如图,由=+可知M,B,C三点共线,令=λ ,则
=+=+λ=+λ(-)=(1-λ)+λ λ=,
所以=,即面积之比为1∶4.
13.解:=+=+=a+(b-a)=a+b;
=+=+=a+(b-a)=a+b;=+=+=a+(b-a)
=a+b.
14.解:如图所示,∵=e2,且=k,∴=k=ke2.
又∵+++=0,
∴=---=-++=e1+(k-1)e2.
又∵+++=0,且=-,=,
∴=---=-++=e2.
15.解:(1)证明:若a,b共线,则存在λ∈R,使a=λb,则e1-2e2=λ(e1+3e2).
由e1,e2不共线,得
∴λ不存在,故a与b不共线,∴{a,b}可以作为一个基底.
(2)设c=ma+nb(m,n∈R),则3e1-e2=m(e1-2e2)+n(e1+3e2)=(m+n)e1+(-2m+3n)e2.
∴ ∴c=2a+b.
(3)由4e1-3e2=λa+μb,得4e1-3e2=λ(e1-2e2)+μ(e1+3e2)=(λ+μ)e1+(-2λ+3μ)e2.
∴ 故所求λ,μ的值分别为3和1.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
