高中数学人教A版(2019)选择性必修第一册空间向量与立体几何1(Word含答案解析)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册空间向量与立体几何1(Word含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 20:51:23 | ||
图片预览




文档简介
高中数学人教A版(2019)选择性必修第一册
——空间向量与立体几何
一、单选题
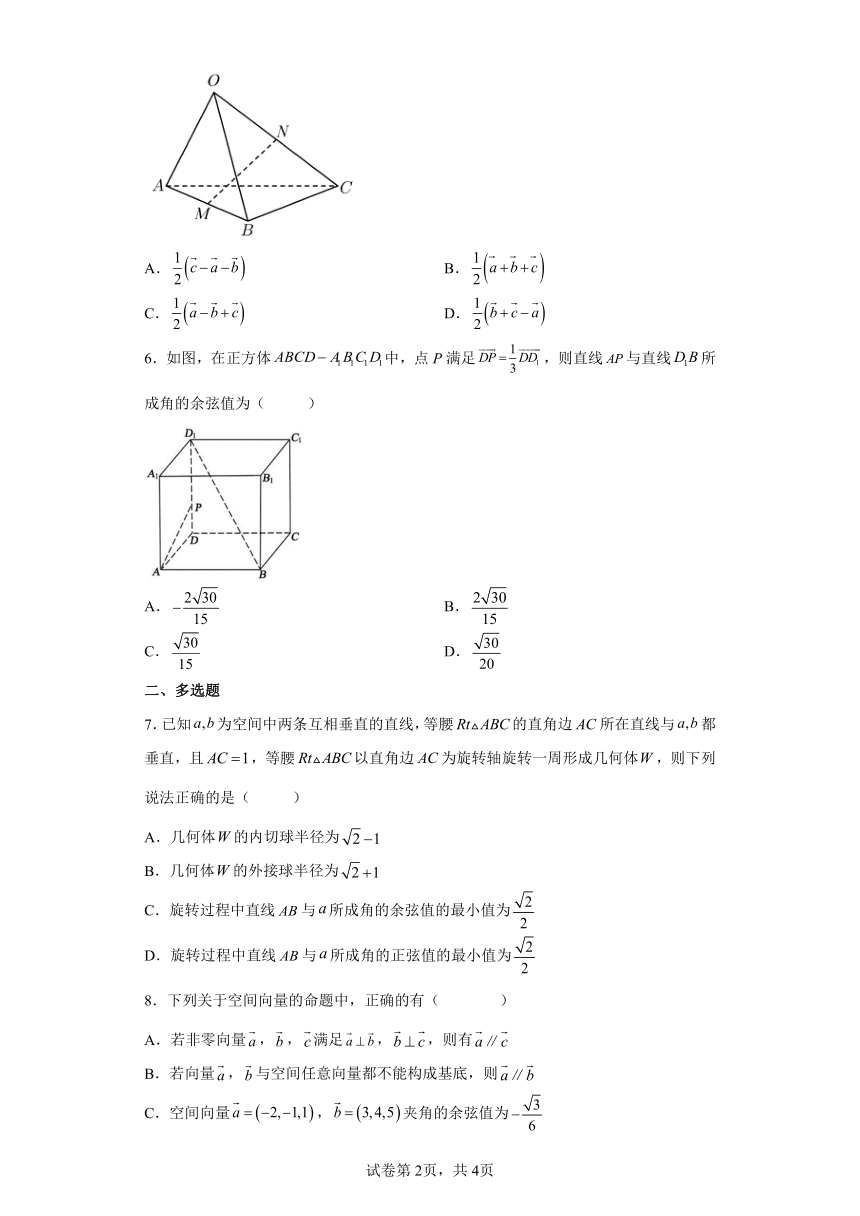
1.如图,在四面体OABC中,,,,点在线段上,且,为的中点,则等于( )
A. B.
C. D.
2.如图,在三棱锥中,平面ABC,是边长为2的正三角形,,E,F分别为MA,MC的中点,则异面直线BE与AF所成角的余弦值为( )
A. B. C. D.
3.已知,,若,则实数的值为( )
A. B. C. D.
4.已知平行六面体中,,,,,.则的长为( )
A. B. C.12 D.
5.如图所示,已知三棱锥,点,分别为,的中点,且,,,用,,表示,则等于( )
A. B.
C. D.
6.如图,在正方体中,点P满足,则直线与直线所成角的余弦值为( )
A. B.
C. D.
二、多选题
7.已知为空间中两条互相垂直的直线,等腰的直角边所在直线与都垂直,且,等腰以直角边为旋转轴旋转一周形成几何体,则下列说法正确的是( )
A.几何体的内切球半径为
B.几何体的外接球半径为
C.旋转过程中直线与所成角的余弦值的最小值为
D.旋转过程中直线与所成角的正弦值的最小值为
8.下列关于空间向量的命题中,正确的有( )
A.若非零向量,,满足,,则有
B.若向量,与空间任意向量都不能构成基底,则
C.空间向量,夹角的余弦值为
D.已知,,若与垂直,则
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.如图,正四棱锥的棱长均为2,点E为侧棱PD的中点.若点M,N分别为直线AB,CE上的动点,则MN的最小值为______.
10.在棱长为1的正方体中,过点A的平面分别与棱,,交于点E,F,G,记四边形AEFG在平面上的正投影的面积为,四边形AEFG在平面上的正投影的面积为.
给出下面四个结论:
①四边形AEFG是平行四边形;
②的最大值为2;
③的最大值为;
④四边形AEFG可以是菱形,且菱形面积的最大值为.
则其中所有正确结论的序号是___________.
11.设直线的方向向量分别为,若,则实数m等于___________.
12.已知空间直角坐标系中,点,,若,与同向,则向量的坐标为______.
四、解答题
13.如图,在直四棱柱中,底面ABCD是菱形,,,,E,F,G分别为,,的中点.
(1)若,求证:平面;
(2)若直线FG与平面BOE所成角的正弦值为,求平面BOE与平面所成的锐二面角的余弦值.
14.已知是平面的一条斜线且B为斜足,设的射影是,而l是与平面平行的一条直线.判断下列命题是否成立,并用空间向量证明:
(1)当时,;
(2)当时,.
15.如图,在四棱锥中,底面为正方形,,且,E为中点.
(1)证明:;
(2)若,求与平面所成角的正弦值.
16.空间向量,,不共面是否可以推出其中任意两个向量均不平行?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用空间向量的加法与减法可得出关于、、的表达式.
【详解】
.
故选:D.
2.B
【解析】
【分析】
解法一设H为MF的中点,连接EH,BH,由E是MA的中点知,,进而得到是异面直线BE与AF所成的角或其补角,根据已知条件计算出的各边长,再利用余弦定理即可求出的余弦值,从而可得异面直线BE与AF所成角的余弦值;
解法二建立空间直角坐标系,写出相关点及向量的坐标,利用向量的夹角公式即可得解.
【详解】
解法一:设H为MF的中点,连接EH,BH,如图,
∵E是MA的中点,
∴,.
∴是异面直线BE与AF所成的角或其补角.
∵平面ABC,∴,,
∵,,
∴,
∴.
∵F为MC的中点,
∴,,
又,
∴在中,,
,
∴,
∴异面直线BE与AF所成角的余弦值为,
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,,,,
所以,,
则,
∴异面直线BE与AF所成角的余弦值为,
故选:B.
3.C
【解析】
【分析】
根据,可知,再根据空间向量数量积的坐标运算,即可求出结果.
【详解】
因为,所以,即,
所以.
故选:C.
4.A
【解析】
【分析】
由,可得,再利用数量积运算性质即可得出.
【详解】
,,,,
,.
,
,
,
即的长为.
故选:A.
5.A
【解析】
【分析】
连接,先根据已知条件表示出,再根据求得结果.
【详解】
连接,如下图所示:
因为为的中点,所以,
又因为为的中点,所以,
所以,
故选:A.
6.B
【解析】
【分析】
建立空间直角坐标系,求出向量,利用向量的夹角公式求得,结合异面直线所成角的范围可得答案.
【详解】
如图,以D为坐标原点,DA为x轴,DC为y轴, 为z轴,建立空间直角坐标系,设正方体棱长为3,
则 ,
则 ,
故 ,
故直线与直线所成角的余弦值为 ,
故选:B
7.AD
【解析】
【分析】
根据题意直接求几何体的内切球半径和外接球半径,判断AB,由于三条直线两两相互垂直,所以如图,以坐标原点,以为轴,为轴,为轴,建立空间直角坐标系,利用空间向量求旋转过程中直线与所成角,从而可判断CD,
【详解】
等腰以直角边为旋转轴旋转一周形成几何体圆锥,且,所以其外接球的球心为,半径为,所以B错误,设其内切球的半径为,则由题意可得,解得,即内切球半径为,所以A正确
由题意知,三条直线两两相互垂直,画出图形如图,由,,
斜边以直线为旋转轴,则点保持不变,点的运动轨迹是以为圆心,1为半径的圆,
以坐标原点,以为轴,为轴,为轴,建立空间直角坐标系,
则,直线的方向单位向量,直线的方向单位向量,
设点在运动过程中的坐标中的坐标,其中为与的夹角,,
∴,设与所成夹角为,
则,
∴,
∴C错误,D正确,
故答案为:AD
8.BCD
【解析】
【分析】
对于A:与的位置关系不确定,根据空间向量基本定理判断B,根据空间向量夹角的坐标运算判断C,求出与的坐标,再根据得到方程,解得即可;
【详解】
解:对于A,若非零向量满足,则与的位置关系不确定,也有可能平行,故A错误;
对于B,若向量与空间任意向量都不能构成基底,则只能两个向量是共线向量,故,故B正确;
对于C:因为,,所以,,,设与的夹角为,则,故C正确;
对于D:因为,,所以,,因为与垂直,所以,即,解得,故D正确;
故选:BCD
9.
【解析】
【分析】
根据题意,先建立空间直角坐标系,然后写出相关点的坐标,再写出相关的向量,然后根据点分别为直线上写出点的坐标,这样就得到,然后根据的取值范围而确定
【详解】
建立如图所示的空间直角坐标系,则有:
,,,,,
可得:
设,且
则有:,
可得:
则有:
故
则当且仅当时,
故答案为:
10.①③④
【解析】
【分析】
对①,根据面面平行的性质定理即可判断答案;
建立空间直角坐标系,设,然后根据①得到的关系,进而判断②,然后结合基本不等式判断③,最后根据菱形的对角线互相垂直判断④.
【详解】
对①,因为平面AEFG分别与平面、平面、平面、平面交于,易知平面∥平面,则,而平面∥平面,则,所以四边形AEFG是平行四边形.①正确;
以A为原点,分别为轴建立空间直角坐标系,记点G在平面上的投影点为点H,点F,G在平面上的投影点分别为点I,J.设,其中,则,,所以,由①,,则
.
易得,,所以,②错误;
,当且仅当时取“=”,③正确;
,令,即, 则此时,平行四边形AEFG是菱形,而此时,所以菱形的面积,当时,.④正确.
故答案为:①③④.
11.2
【解析】
【分析】
根据向量垂直与数量积的等价关系,,计算即可.
【详解】
因为,则其方向向量,
,解得.
故答案为:2.
12.
【解析】
【分析】
求出坐标,根据给条件表示出坐标,利用向量模的坐标表示计算作答.
【详解】
因,,则,
因与同向,则设,因此,,
于是得,解得,则,
所以向量的坐标为.
故答案为:
13.(1)证明见解析
(2)或
【解析】
【分析】
(1)连接FD,先在中,由证得,再连接,,由得到,最后结合线面垂直的判定定理即可得证;
(2)建立空间直角坐标系,求出相关平面的法向量和直线的方向向量,再由向量的夹角公式即可得解.
(1)
因为底面ABCD是菱形,,,所以,,
连接OF,因为O,F分别为AC,的中点,所以平面ABCD,
因为,所以,连接DF,则,
所以,所以.
连接,,易知,所以,
因为,平面,平面,所以平面.
(2)
由(1)得AC,BD,OF两两垂直,故以O为坐标原点,OA,OB,OF所在直线分别为x轴 y轴 z轴建立如图所示的空间直角坐标系,
设,则,,,,,,,,,.
设平面BOE的法向量为,则有,即,则,取,则,
所以.
设直线FG与平面BOE所成的角为,
则,(技巧:线面角的正弦值即平面的法向量与直线方向向量夹角的余弦值的绝对值)
得或.
设平面的法向量为,则,
即,取,则,,所以.
设平面BOE与平面所成的锐二面角为,
则,
当时,;当时,.
综上,平面BOE与平面所成的锐二面角的余弦值为或.
【点睛】
用向量法求空间角的关键:
①建系,根据几何体的结构特征与已知条件找出或作出共点的两两垂直的三条直线,建立适当的空间直角坐标系.
②求向量,求出相关点的坐标 直线的方向向量 平面的法向量等.
③用公式,由向量夹角公式求出两个向量夹角的余弦值.
④巧转化,根据向量夹角与空间角的关系,将向量夹角转化为所求的空间角.若直线a,b的方向向量分别为,,平面,的法向量分别为,,则有:
(1)设直线a,b所成角为,则;
(2)设直线a与平面所成的角为,则;
(3)设平面,所成的角为,则(需要根据几何体的结构特征判断二面角是锐二面角还是钝二面角).
14.(1)成立,证明见解析
(2)成立,证明见解析
【解析】
【分析】
(1)依题意:,,∴,再假设相应的方向向量,利用向量中两个向量垂直的表示方法即可证明.
(2)与(1)的分析方法相同.
(1)
按照题意,作图如下:
∵,是的一个法向量,设l的方向向量为,则,
由已知,,由图可知,
∴,即,故命题成立;
(2)
按照题意,作图如下:
∵,是的一个法向量,设l的方向向量为,由题可知=0,
∴,而,
∴,故命题成立;
15.(1)证明见解析
(2)
【解析】
【分析】
(1)易证平面,再由,得到,再根据,E为中点,得到,然后利用线面垂直的判定定理证明;
(2)过点D作的垂线,交于点F,易知两两互相垂直,建立空间直角坐标系,因为平面,则是平面PBC的一个法向量,然后由求解.
(1)
证明:∵底面为正方形,
∴
又,即,且,平面,平面,
∴平面.
∵平面,
∴,
∵,∴.
∵,E为中点,
∴.
又,平面,平面,
∴平面.
又平面,
∴.
(2)
解:在平面内,过点D作的垂线,交于点F.
由(1)知,平面,平面,∴.
∴两两互相垂直,
∴以点D为空间坐标原点,为x轴,为y轴,为x轴,建立空间直角坐标系.
由,,可知,,,
∴,.
由(1)知,平面,
∴.
∴与平面所成角的正弦值为.
16.可以
【解析】
【分析】
根据空间向量的基底的定义,即可求解.
【详解】
由题意,空间向量,,不共面,可得向量,,可以构成一个空间基底,
所以其中任意两个向量均不平行.
答案第1页,共2页
答案第1页,共2页
——空间向量与立体几何
一、单选题
1.如图,在四面体OABC中,,,,点在线段上,且,为的中点,则等于( )
A. B.
C. D.
2.如图,在三棱锥中,平面ABC,是边长为2的正三角形,,E,F分别为MA,MC的中点,则异面直线BE与AF所成角的余弦值为( )
A. B. C. D.
3.已知,,若,则实数的值为( )
A. B. C. D.
4.已知平行六面体中,,,,,.则的长为( )
A. B. C.12 D.
5.如图所示,已知三棱锥,点,分别为,的中点,且,,,用,,表示,则等于( )
A. B.
C. D.
6.如图,在正方体中,点P满足,则直线与直线所成角的余弦值为( )
A. B.
C. D.
二、多选题
7.已知为空间中两条互相垂直的直线,等腰的直角边所在直线与都垂直,且,等腰以直角边为旋转轴旋转一周形成几何体,则下列说法正确的是( )
A.几何体的内切球半径为
B.几何体的外接球半径为
C.旋转过程中直线与所成角的余弦值的最小值为
D.旋转过程中直线与所成角的正弦值的最小值为
8.下列关于空间向量的命题中,正确的有( )
A.若非零向量,,满足,,则有
B.若向量,与空间任意向量都不能构成基底,则
C.空间向量,夹角的余弦值为
D.已知,,若与垂直,则
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.如图,正四棱锥的棱长均为2,点E为侧棱PD的中点.若点M,N分别为直线AB,CE上的动点,则MN的最小值为______.
10.在棱长为1的正方体中,过点A的平面分别与棱,,交于点E,F,G,记四边形AEFG在平面上的正投影的面积为,四边形AEFG在平面上的正投影的面积为.
给出下面四个结论:
①四边形AEFG是平行四边形;
②的最大值为2;
③的最大值为;
④四边形AEFG可以是菱形,且菱形面积的最大值为.
则其中所有正确结论的序号是___________.
11.设直线的方向向量分别为,若,则实数m等于___________.
12.已知空间直角坐标系中,点,,若,与同向,则向量的坐标为______.
四、解答题
13.如图,在直四棱柱中,底面ABCD是菱形,,,,E,F,G分别为,,的中点.
(1)若,求证:平面;
(2)若直线FG与平面BOE所成角的正弦值为,求平面BOE与平面所成的锐二面角的余弦值.
14.已知是平面的一条斜线且B为斜足,设的射影是,而l是与平面平行的一条直线.判断下列命题是否成立,并用空间向量证明:
(1)当时,;
(2)当时,.
15.如图,在四棱锥中,底面为正方形,,且,E为中点.
(1)证明:;
(2)若,求与平面所成角的正弦值.
16.空间向量,,不共面是否可以推出其中任意两个向量均不平行?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用空间向量的加法与减法可得出关于、、的表达式.
【详解】
.
故选:D.
2.B
【解析】
【分析】
解法一设H为MF的中点,连接EH,BH,由E是MA的中点知,,进而得到是异面直线BE与AF所成的角或其补角,根据已知条件计算出的各边长,再利用余弦定理即可求出的余弦值,从而可得异面直线BE与AF所成角的余弦值;
解法二建立空间直角坐标系,写出相关点及向量的坐标,利用向量的夹角公式即可得解.
【详解】
解法一:设H为MF的中点,连接EH,BH,如图,
∵E是MA的中点,
∴,.
∴是异面直线BE与AF所成的角或其补角.
∵平面ABC,∴,,
∵,,
∴,
∴.
∵F为MC的中点,
∴,,
又,
∴在中,,
,
∴,
∴异面直线BE与AF所成角的余弦值为,
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,,,,
所以,,
则,
∴异面直线BE与AF所成角的余弦值为,
故选:B.
3.C
【解析】
【分析】
根据,可知,再根据空间向量数量积的坐标运算,即可求出结果.
【详解】
因为,所以,即,
所以.
故选:C.
4.A
【解析】
【分析】
由,可得,再利用数量积运算性质即可得出.
【详解】
,,,,
,.
,
,
,
即的长为.
故选:A.
5.A
【解析】
【分析】
连接,先根据已知条件表示出,再根据求得结果.
【详解】
连接,如下图所示:
因为为的中点,所以,
又因为为的中点,所以,
所以,
故选:A.
6.B
【解析】
【分析】
建立空间直角坐标系,求出向量,利用向量的夹角公式求得,结合异面直线所成角的范围可得答案.
【详解】
如图,以D为坐标原点,DA为x轴,DC为y轴, 为z轴,建立空间直角坐标系,设正方体棱长为3,
则 ,
则 ,
故 ,
故直线与直线所成角的余弦值为 ,
故选:B
7.AD
【解析】
【分析】
根据题意直接求几何体的内切球半径和外接球半径,判断AB,由于三条直线两两相互垂直,所以如图,以坐标原点,以为轴,为轴,为轴,建立空间直角坐标系,利用空间向量求旋转过程中直线与所成角,从而可判断CD,
【详解】
等腰以直角边为旋转轴旋转一周形成几何体圆锥,且,所以其外接球的球心为,半径为,所以B错误,设其内切球的半径为,则由题意可得,解得,即内切球半径为,所以A正确
由题意知,三条直线两两相互垂直,画出图形如图,由,,
斜边以直线为旋转轴,则点保持不变,点的运动轨迹是以为圆心,1为半径的圆,
以坐标原点,以为轴,为轴,为轴,建立空间直角坐标系,
则,直线的方向单位向量,直线的方向单位向量,
设点在运动过程中的坐标中的坐标,其中为与的夹角,,
∴,设与所成夹角为,
则,
∴,
∴C错误,D正确,
故答案为:AD
8.BCD
【解析】
【分析】
对于A:与的位置关系不确定,根据空间向量基本定理判断B,根据空间向量夹角的坐标运算判断C,求出与的坐标,再根据得到方程,解得即可;
【详解】
解:对于A,若非零向量满足,则与的位置关系不确定,也有可能平行,故A错误;
对于B,若向量与空间任意向量都不能构成基底,则只能两个向量是共线向量,故,故B正确;
对于C:因为,,所以,,,设与的夹角为,则,故C正确;
对于D:因为,,所以,,因为与垂直,所以,即,解得,故D正确;
故选:BCD
9.
【解析】
【分析】
根据题意,先建立空间直角坐标系,然后写出相关点的坐标,再写出相关的向量,然后根据点分别为直线上写出点的坐标,这样就得到,然后根据的取值范围而确定
【详解】
建立如图所示的空间直角坐标系,则有:
,,,,,
可得:
设,且
则有:,
可得:
则有:
故
则当且仅当时,
故答案为:
10.①③④
【解析】
【分析】
对①,根据面面平行的性质定理即可判断答案;
建立空间直角坐标系,设,然后根据①得到的关系,进而判断②,然后结合基本不等式判断③,最后根据菱形的对角线互相垂直判断④.
【详解】
对①,因为平面AEFG分别与平面、平面、平面、平面交于,易知平面∥平面,则,而平面∥平面,则,所以四边形AEFG是平行四边形.①正确;
以A为原点,分别为轴建立空间直角坐标系,记点G在平面上的投影点为点H,点F,G在平面上的投影点分别为点I,J.设,其中,则,,所以,由①,,则
.
易得,,所以,②错误;
,当且仅当时取“=”,③正确;
,令,即, 则此时,平行四边形AEFG是菱形,而此时,所以菱形的面积,当时,.④正确.
故答案为:①③④.
11.2
【解析】
【分析】
根据向量垂直与数量积的等价关系,,计算即可.
【详解】
因为,则其方向向量,
,解得.
故答案为:2.
12.
【解析】
【分析】
求出坐标,根据给条件表示出坐标,利用向量模的坐标表示计算作答.
【详解】
因,,则,
因与同向,则设,因此,,
于是得,解得,则,
所以向量的坐标为.
故答案为:
13.(1)证明见解析
(2)或
【解析】
【分析】
(1)连接FD,先在中,由证得,再连接,,由得到,最后结合线面垂直的判定定理即可得证;
(2)建立空间直角坐标系,求出相关平面的法向量和直线的方向向量,再由向量的夹角公式即可得解.
(1)
因为底面ABCD是菱形,,,所以,,
连接OF,因为O,F分别为AC,的中点,所以平面ABCD,
因为,所以,连接DF,则,
所以,所以.
连接,,易知,所以,
因为,平面,平面,所以平面.
(2)
由(1)得AC,BD,OF两两垂直,故以O为坐标原点,OA,OB,OF所在直线分别为x轴 y轴 z轴建立如图所示的空间直角坐标系,
设,则,,,,,,,,,.
设平面BOE的法向量为,则有,即,则,取,则,
所以.
设直线FG与平面BOE所成的角为,
则,(技巧:线面角的正弦值即平面的法向量与直线方向向量夹角的余弦值的绝对值)
得或.
设平面的法向量为,则,
即,取,则,,所以.
设平面BOE与平面所成的锐二面角为,
则,
当时,;当时,.
综上,平面BOE与平面所成的锐二面角的余弦值为或.
【点睛】
用向量法求空间角的关键:
①建系,根据几何体的结构特征与已知条件找出或作出共点的两两垂直的三条直线,建立适当的空间直角坐标系.
②求向量,求出相关点的坐标 直线的方向向量 平面的法向量等.
③用公式,由向量夹角公式求出两个向量夹角的余弦值.
④巧转化,根据向量夹角与空间角的关系,将向量夹角转化为所求的空间角.若直线a,b的方向向量分别为,,平面,的法向量分别为,,则有:
(1)设直线a,b所成角为,则;
(2)设直线a与平面所成的角为,则;
(3)设平面,所成的角为,则(需要根据几何体的结构特征判断二面角是锐二面角还是钝二面角).
14.(1)成立,证明见解析
(2)成立,证明见解析
【解析】
【分析】
(1)依题意:,,∴,再假设相应的方向向量,利用向量中两个向量垂直的表示方法即可证明.
(2)与(1)的分析方法相同.
(1)
按照题意,作图如下:
∵,是的一个法向量,设l的方向向量为,则,
由已知,,由图可知,
∴,即,故命题成立;
(2)
按照题意,作图如下:
∵,是的一个法向量,设l的方向向量为,由题可知=0,
∴,而,
∴,故命题成立;
15.(1)证明见解析
(2)
【解析】
【分析】
(1)易证平面,再由,得到,再根据,E为中点,得到,然后利用线面垂直的判定定理证明;
(2)过点D作的垂线,交于点F,易知两两互相垂直,建立空间直角坐标系,因为平面,则是平面PBC的一个法向量,然后由求解.
(1)
证明:∵底面为正方形,
∴
又,即,且,平面,平面,
∴平面.
∵平面,
∴,
∵,∴.
∵,E为中点,
∴.
又,平面,平面,
∴平面.
又平面,
∴.
(2)
解:在平面内,过点D作的垂线,交于点F.
由(1)知,平面,平面,∴.
∴两两互相垂直,
∴以点D为空间坐标原点,为x轴,为y轴,为x轴,建立空间直角坐标系.
由,,可知,,,
∴,.
由(1)知,平面,
∴.
∴与平面所成角的正弦值为.
16.可以
【解析】
【分析】
根据空间向量的基底的定义,即可求解.
【详解】
由题意,空间向量,,不共面,可得向量,,可以构成一个空间基底,
所以其中任意两个向量均不平行.
答案第1页,共2页
答案第1页,共2页
