高中数学人教A版(2019)选择性必修第一册__——空间向量与立体几何单元测试卷3 (word含解析)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册__——空间向量与立体几何单元测试卷3 (word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 853.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 08:15:00 | ||
图片预览




文档简介
高中数学人教A版(2019)选择性必修第一册
——空间向量与立体几何
一、单选题
1.已知正方体各棱长均为,为上靠近的三等分点,则直线与直线所成异面夹角的余弦值为( )
A. B. C. D.
2.若直线的一个方向向量为,直线的一个方向向量为,则直线与所成的角为( )
A.30° B.45° C.60° D.90°
3.如图所示,在平行六面体中,为与的交点,则下列向量中与相等的向量是( )
A. B.
C. D.
4.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑(biē nào).如图,在鳖臑中,平面,,分别为,的中点,,则异面直线与所成角的余弦值为( )
A. B. C. D.0
5.已知,,若,则实数的值为( )
A. B. C. D.
6.在空间直角坐标系中,点到点O的距离为( ).
A. B. C. D.
二、多选题
7.如图,在棱长为2的正方体中,E为的中点F为的中点,如图建系,则下列说法正确的有( )
A. B.向量与所成角的余弦值为
C.平面的一个法向量是 D.点D到直线的距离为
8.在棱长为1的正方体中,,分别是棱,上的点,则下列结论正确的是( )
A.当时,若,则
B.当是棱的中点时,异面直线与所成角的余弦值为
C.直线与平面所成角的正弦值是
D.若平面,则与的长度之和为1
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.如图,二面角等于,A、是棱l上两点,BD、AC分别在半平面、内,,,且,则CD的长等于________.
10.已知直线过点,,且是直线的一个方向向量,则__________.
11.空间四边形ABCD中,,AD与BC成角,则异面直线AB与CD所成角的大小为___________.
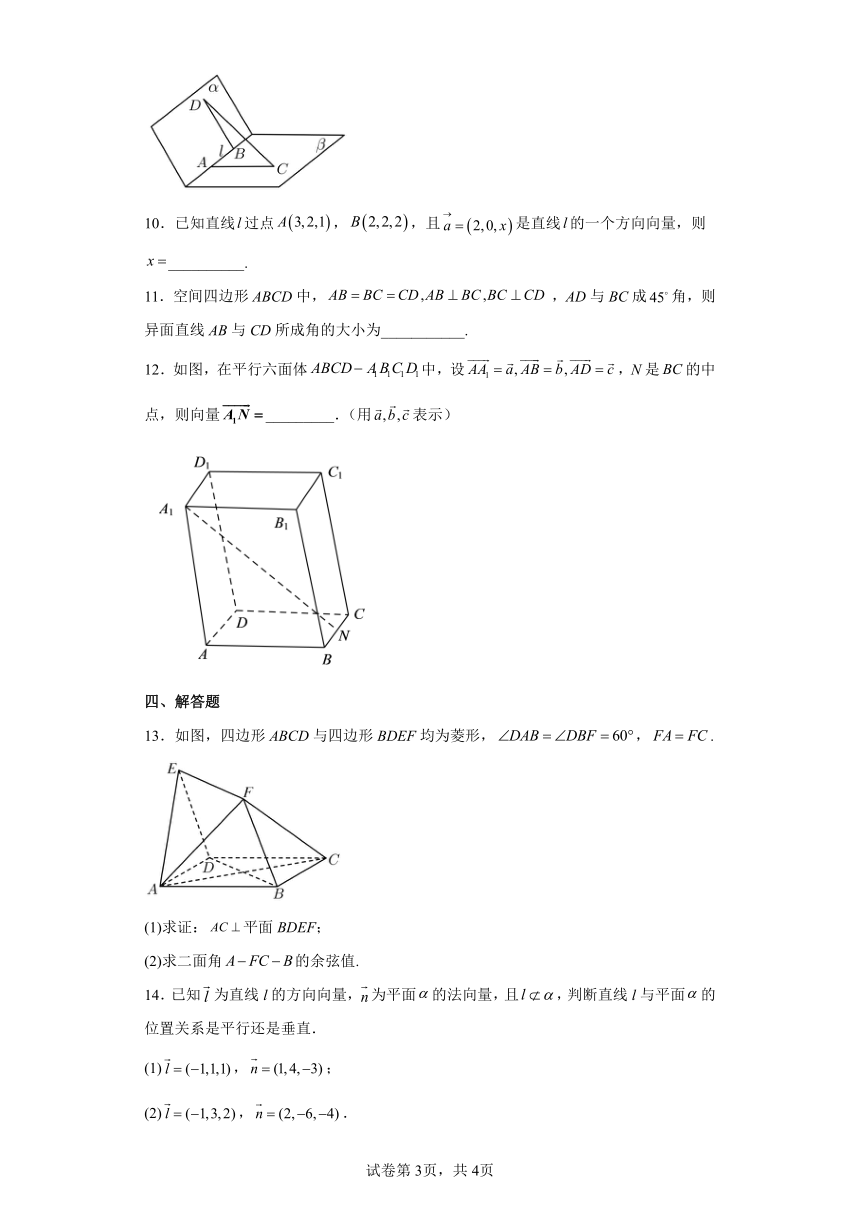
12.如图,在平行六面体中,设,N是的中点,则向量_________.(用表示)
四、解答题
13.如图,四边形ABCD与四边形BDEF均为菱形,,.
(1)求证:平面BDEF;
(2)求二面角的余弦值.
14.已知为直线l的方向向量,为平面的法向量,且,判断直线l与平面的位置关系是平行还是垂直.
(1),;
(2),.
15.如图,三棱锥中,面与面互相垂直,且.求:
(1)所在直线和平面所成角的大小;
(2)所在直线与直线所成角的大小;
(3)二面角的余弦值.
16.已知O为坐标原点,是四面体,,直线与直线平行,并且与坐标平面相交于点D,求点D的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
建立空间直角坐标系,利用空间向量来求异面直线所成的角即可.
【详解】
如图,建立空间直角坐标系,
,0,,,2,,,0,,,,,
,,,,2,,
,
所以直线与直线所成异面夹角的余弦值为,
故选:B.
2.C
【解析】
【分析】
直接由公式,计算两直线的方向向量的夹角,进而得出直线与所成角的大小.
【详解】
因为,,
所以,
所以,
所以直线与所成角的大小为.
故选:C.
3.A
【解析】
【分析】
根据平行六面体的特征和空间向量的线性运算依次对选项的式子变形,即可判断.
【详解】
A:
,故A正确;
B:
,故B错误;
C:
,故C错误;
D:
,故D错误;
故选:A
4.A
【解析】
【分析】
以B点为原点建立空间直角坐标系,用向量法可解.
【详解】
由题意得,为直角三角形,且,建立如图所示的空间直角坐标系,则,,,,,则,.设异面直线与所成角为,则.
故选:A.
5.C
【解析】
【分析】
根据,可知,再根据空间向量数量积的坐标运算,即可求出结果.
【详解】
因为,所以,即,
所以.
故选:C.
6.D
【解析】
【分析】
利用空间两点间的距离公式直接求得答案.
【详解】
点到点O的距离 ,
故选:D
7.BCD
【解析】
【分析】
A选项,利用空间向量表示出,进而求出;B选项,利用空间向量夹角公式求解;C选项,利用数量积为0进行证明线线垂直,进而得到答案;D选项,利用点到直线的空间向量公式进行求解.
【详解】
,,,,所以,所以,故,A错误;
,B正确;
设,则,,而,所以平面的一个法向量是,C正确;
,,则,所以,故点D到直线的距离为,故D正确.
故选:BCD
8.BD
【解析】
【分析】
根据空间向量运算可判断A;建立空间直角坐标系,根据直线夹角的向量公式即可判断B;根据线面夹角的向量公式即可判断C;若平面,只需,利用坐标运算即可判断D.
【详解】
对于选项A,,,所以,所以A错误;
对于选项B,以,,分别为轴,轴,轴建立空间直角坐标系.
当是棱的中点时,,,,,,
,,所以B正确;
对于选项C,易知是平面的一个法向量.,,,
,,所以与平面所成角的
正弦值为,故C错误;
对于选项D,设,,则,,,
又,,.由于,故若平面,
只需,所以,D正确.
故选:BD.
9.4
【解析】
【分析】
根据二面角的定义,结合空间向量加法运算性质、空间向量数量积的运算性质进行求解即可.
【详解】
由二面角的平面角的定义知,
∴,
由,,得,,又,
∴
,
所以,即.
故答案为:4.
10.
【解析】
【分析】
由题得,解方程组即得解.
【详解】
解:由题得,
因为是直线的一个方向向量,
所以,所以,
所以.
故答案为:
11.
【解析】
【分析】
由空间向量的运算得出,进而由余弦定理得出,最后由向量法得出异面直线AB与CD所成角的大小.
【详解】
,
不妨设,则
设异面直线AB与CD所成角为,则
,.
故答案为:
12.
【解析】
【分析】
根据向量的加减法运算法则及数乘运算求解即可.
【详解】
由向量的减法及加法运算可得,
,
故答案为:
13.(1)证明见解析
(2)
【解析】
【分析】
(1)设AC交BD于点O,连接FO,证明,,根据线面垂直的判定定理即可得证;
(2)连接DF,证明平面ABCD,以OA,OB,OF为x轴,y轴,z轴建立空间直角坐标系,利用向量法即可得出答案.
(1)
证明:设AC交BD于点O,连接FO,
∵四边形ABCD为菱形,∴,O为AC中点,
又∵,∴,又,
平面BDEF,平面BDEF,
∴平面BDEF;
(2)
解:如图,连接DF,
∵四边形BDEF为菱形,,
∴为等边三角形,
又∵O为BD中点,∴,
又,,平面ABCD,平面ABCD,
∴平面ABCD,
分别以OA,OB,OF为x轴,y轴,z轴建立空间直角坐标系如图所示,
设,则,,
又∴为等边三角形,
∴,∴点,,,
,,
∴,,
设平面BCF的一个法量,
则,
令,得,
∵平面ABCD,平面ABCD,
所以,
又因为,,
所以平面AFC,
则即为平面AFC的一个法向量,
∴,
又二面角的平面角是锐角,
∴二面角的余弦值为.
14.(1)平行
(2)垂直
【解析】
【分析】
(1)由直线方向向量与平面的法向量垂直,得线面平行;
(2)由直线方向向量与平面的法向量平行,得线面垂直.
(1)
,,又,所以.
(2)
,即,所以.
15.(1)
(2)
(3)
【解析】
【分析】
(1)建立空间直角坐标系,利用向量法求得直线与平面所成角的大小.
(2)利用向量法求得直线与直线所成角的大小.
(3)利用向量法求得二面角的余弦值.
(1)
依题意,平面平面,.
以为原点建立如图所示空间直角坐标系,
设,则,.
平面的法向量为,设与平面所成角为,
则,由于,所以.
(2)
,所以,所以与所成角为.
(3)
设平面的法向量为,
则,故可设.
设二面角的大小为,由图可知为钝角,
.
16.
【解析】
【分析】
设点的坐标为,0,,则,,,,,,由直线,能求出点的坐标.
【详解】
由题意可设点的坐标为,0,,
则,,,,,,
直线,
,解得,,
点的坐标为,0,.
答案第1页,共2页
答案第1页,共2页
——空间向量与立体几何
一、单选题
1.已知正方体各棱长均为,为上靠近的三等分点,则直线与直线所成异面夹角的余弦值为( )
A. B. C. D.
2.若直线的一个方向向量为,直线的一个方向向量为,则直线与所成的角为( )
A.30° B.45° C.60° D.90°
3.如图所示,在平行六面体中,为与的交点,则下列向量中与相等的向量是( )
A. B.
C. D.
4.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑(biē nào).如图,在鳖臑中,平面,,分别为,的中点,,则异面直线与所成角的余弦值为( )
A. B. C. D.0
5.已知,,若,则实数的值为( )
A. B. C. D.
6.在空间直角坐标系中,点到点O的距离为( ).
A. B. C. D.
二、多选题
7.如图,在棱长为2的正方体中,E为的中点F为的中点,如图建系,则下列说法正确的有( )
A. B.向量与所成角的余弦值为
C.平面的一个法向量是 D.点D到直线的距离为
8.在棱长为1的正方体中,,分别是棱,上的点,则下列结论正确的是( )
A.当时,若,则
B.当是棱的中点时,异面直线与所成角的余弦值为
C.直线与平面所成角的正弦值是
D.若平面,则与的长度之和为1
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.如图,二面角等于,A、是棱l上两点,BD、AC分别在半平面、内,,,且,则CD的长等于________.
10.已知直线过点,,且是直线的一个方向向量,则__________.
11.空间四边形ABCD中,,AD与BC成角,则异面直线AB与CD所成角的大小为___________.
12.如图,在平行六面体中,设,N是的中点,则向量_________.(用表示)
四、解答题
13.如图,四边形ABCD与四边形BDEF均为菱形,,.
(1)求证:平面BDEF;
(2)求二面角的余弦值.
14.已知为直线l的方向向量,为平面的法向量,且,判断直线l与平面的位置关系是平行还是垂直.
(1),;
(2),.
15.如图,三棱锥中,面与面互相垂直,且.求:
(1)所在直线和平面所成角的大小;
(2)所在直线与直线所成角的大小;
(3)二面角的余弦值.
16.已知O为坐标原点,是四面体,,直线与直线平行,并且与坐标平面相交于点D,求点D的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
建立空间直角坐标系,利用空间向量来求异面直线所成的角即可.
【详解】
如图,建立空间直角坐标系,
,0,,,2,,,0,,,,,
,,,,2,,
,
所以直线与直线所成异面夹角的余弦值为,
故选:B.
2.C
【解析】
【分析】
直接由公式,计算两直线的方向向量的夹角,进而得出直线与所成角的大小.
【详解】
因为,,
所以,
所以,
所以直线与所成角的大小为.
故选:C.
3.A
【解析】
【分析】
根据平行六面体的特征和空间向量的线性运算依次对选项的式子变形,即可判断.
【详解】
A:
,故A正确;
B:
,故B错误;
C:
,故C错误;
D:
,故D错误;
故选:A
4.A
【解析】
【分析】
以B点为原点建立空间直角坐标系,用向量法可解.
【详解】
由题意得,为直角三角形,且,建立如图所示的空间直角坐标系,则,,,,,则,.设异面直线与所成角为,则.
故选:A.
5.C
【解析】
【分析】
根据,可知,再根据空间向量数量积的坐标运算,即可求出结果.
【详解】
因为,所以,即,
所以.
故选:C.
6.D
【解析】
【分析】
利用空间两点间的距离公式直接求得答案.
【详解】
点到点O的距离 ,
故选:D
7.BCD
【解析】
【分析】
A选项,利用空间向量表示出,进而求出;B选项,利用空间向量夹角公式求解;C选项,利用数量积为0进行证明线线垂直,进而得到答案;D选项,利用点到直线的空间向量公式进行求解.
【详解】
,,,,所以,所以,故,A错误;
,B正确;
设,则,,而,所以平面的一个法向量是,C正确;
,,则,所以,故点D到直线的距离为,故D正确.
故选:BCD
8.BD
【解析】
【分析】
根据空间向量运算可判断A;建立空间直角坐标系,根据直线夹角的向量公式即可判断B;根据线面夹角的向量公式即可判断C;若平面,只需,利用坐标运算即可判断D.
【详解】
对于选项A,,,所以,所以A错误;
对于选项B,以,,分别为轴,轴,轴建立空间直角坐标系.
当是棱的中点时,,,,,,
,,所以B正确;
对于选项C,易知是平面的一个法向量.,,,
,,所以与平面所成角的
正弦值为,故C错误;
对于选项D,设,,则,,,
又,,.由于,故若平面,
只需,所以,D正确.
故选:BD.
9.4
【解析】
【分析】
根据二面角的定义,结合空间向量加法运算性质、空间向量数量积的运算性质进行求解即可.
【详解】
由二面角的平面角的定义知,
∴,
由,,得,,又,
∴
,
所以,即.
故答案为:4.
10.
【解析】
【分析】
由题得,解方程组即得解.
【详解】
解:由题得,
因为是直线的一个方向向量,
所以,所以,
所以.
故答案为:
11.
【解析】
【分析】
由空间向量的运算得出,进而由余弦定理得出,最后由向量法得出异面直线AB与CD所成角的大小.
【详解】
,
不妨设,则
设异面直线AB与CD所成角为,则
,.
故答案为:
12.
【解析】
【分析】
根据向量的加减法运算法则及数乘运算求解即可.
【详解】
由向量的减法及加法运算可得,
,
故答案为:
13.(1)证明见解析
(2)
【解析】
【分析】
(1)设AC交BD于点O,连接FO,证明,,根据线面垂直的判定定理即可得证;
(2)连接DF,证明平面ABCD,以OA,OB,OF为x轴,y轴,z轴建立空间直角坐标系,利用向量法即可得出答案.
(1)
证明:设AC交BD于点O,连接FO,
∵四边形ABCD为菱形,∴,O为AC中点,
又∵,∴,又,
平面BDEF,平面BDEF,
∴平面BDEF;
(2)
解:如图,连接DF,
∵四边形BDEF为菱形,,
∴为等边三角形,
又∵O为BD中点,∴,
又,,平面ABCD,平面ABCD,
∴平面ABCD,
分别以OA,OB,OF为x轴,y轴,z轴建立空间直角坐标系如图所示,
设,则,,
又∴为等边三角形,
∴,∴点,,,
,,
∴,,
设平面BCF的一个法量,
则,
令,得,
∵平面ABCD,平面ABCD,
所以,
又因为,,
所以平面AFC,
则即为平面AFC的一个法向量,
∴,
又二面角的平面角是锐角,
∴二面角的余弦值为.
14.(1)平行
(2)垂直
【解析】
【分析】
(1)由直线方向向量与平面的法向量垂直,得线面平行;
(2)由直线方向向量与平面的法向量平行,得线面垂直.
(1)
,,又,所以.
(2)
,即,所以.
15.(1)
(2)
(3)
【解析】
【分析】
(1)建立空间直角坐标系,利用向量法求得直线与平面所成角的大小.
(2)利用向量法求得直线与直线所成角的大小.
(3)利用向量法求得二面角的余弦值.
(1)
依题意,平面平面,.
以为原点建立如图所示空间直角坐标系,
设,则,.
平面的法向量为,设与平面所成角为,
则,由于,所以.
(2)
,所以,所以与所成角为.
(3)
设平面的法向量为,
则,故可设.
设二面角的大小为,由图可知为钝角,
.
16.
【解析】
【分析】
设点的坐标为,0,,则,,,,,,由直线,能求出点的坐标.
【详解】
由题意可设点的坐标为,0,,
则,,,,,,
直线,
,解得,,
点的坐标为,0,.
答案第1页,共2页
答案第1页,共2页
