人教版数学九年级下册 27.3位似课件(共35张PPT)
文档属性
| 名称 | 人教版数学九年级下册 27.3位似课件(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 04:26:20 | ||
图片预览







文档简介
(共35张PPT)
第二十七章 相似
27.3 位似(1)
行 甚 于 言
——清华大学 校训名言
一、新课引入
1、我们学过的图形变换形式有哪些?
2、什么叫相似?相似与全等有什么区别与联系?
平移、旋转、对称
相似:形状相同。
全等:大小、形状相同,能够重合
区别:相似不一定全等,但全等一定相似。
联系:形状相同
1
2
二、学习目标
了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质;
掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
三、研读课文
知识点一
认真阅读课本第59至60页的内容,完成下面练习并体验知识点的形成过程.
1、生活中我们经常把自己好看的照片放大或缩小,由于没有改变图形的形状,我们得到的照片是真实的.
三、研读课文
知识点一
思考 图中多边形相似吗?如果有,那么这种相似有什么特征?
如果两个图形不仅是相似图形,而且是每组对应点连线相交于 ,对应边互相 ,那么这样的两个图形叫做_________.这个点叫做 .(位似中心可在形上、形外、形内.)
位似图形及其有关概念
一点
平行
位似图形
位似中心
三、研读课文
练 一 练
1、下列说法正确的是( )
A. 全等图形一定是位似图形.
B.相似图形一定是位似图形.
C.位似图形一定是全等图形.
D.位似图形是具有某种特殊位置的相似图形.
D
三、研读课文
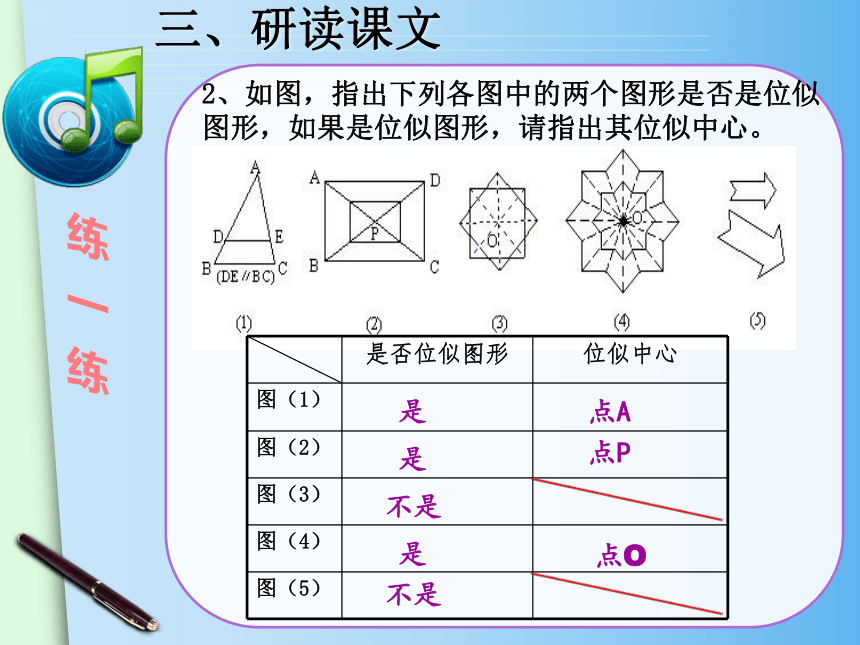
2、如图,指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心。
是否位似图形 位似中心
图(1)
图(2)
图(3)
图(4)
图(5)
是
点A
是
点P
不是
是
点O
不是
练 一 练
三、研读课文
知识点二
分析:把原图形缩小到原来的 ,也就是使新图形上各顶点到位似中心的距离与原图形各对应顶点到位似中心的距离之比为1∶2 。
例2(教材P60例题) 把图1中的四边形ABCD缩小到
原来的 。
图1
位 似 作 图
D
C
B
A
C
D
B
A
●
●
●
●
●
A`
B`
C`
D`
O
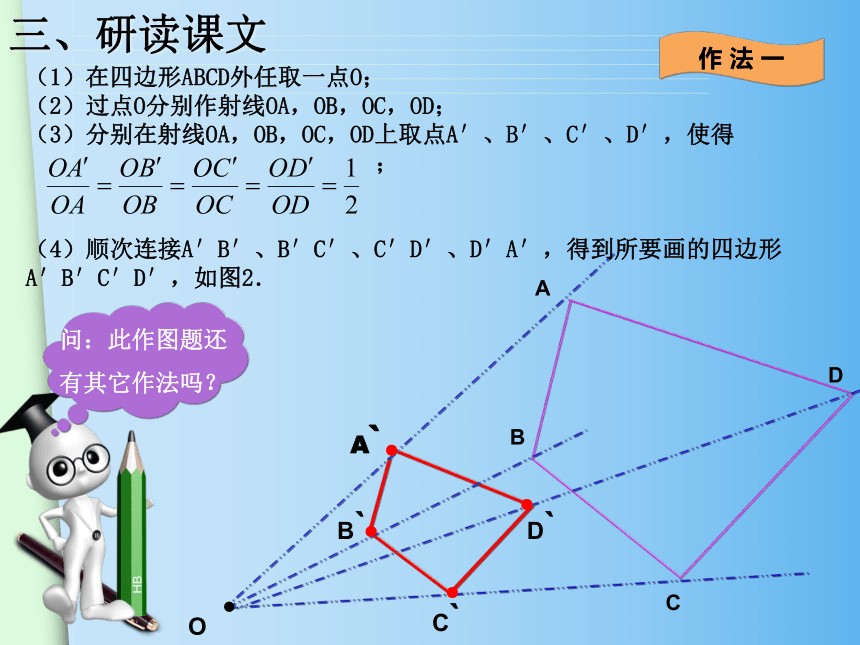
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′、B′、C′、D′,使得
;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′,如图2.
作 法 一
问:此作图题还
有其它作法吗?
三、研读课文
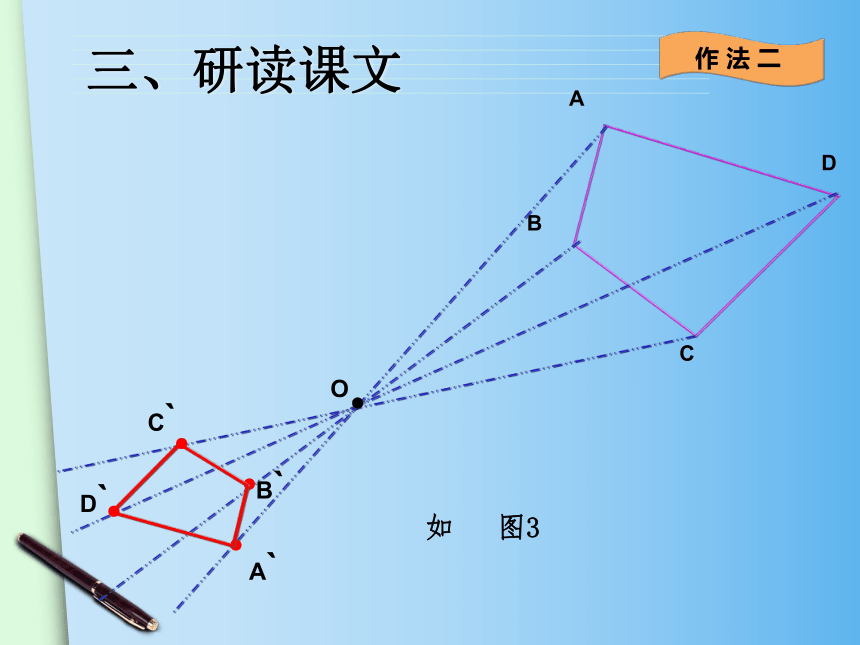
如 图3
作 法 二
D
C
B
A
O
●
●
A`
B`
C`
D`
三、研读课文
●
●
●
三、研读课文
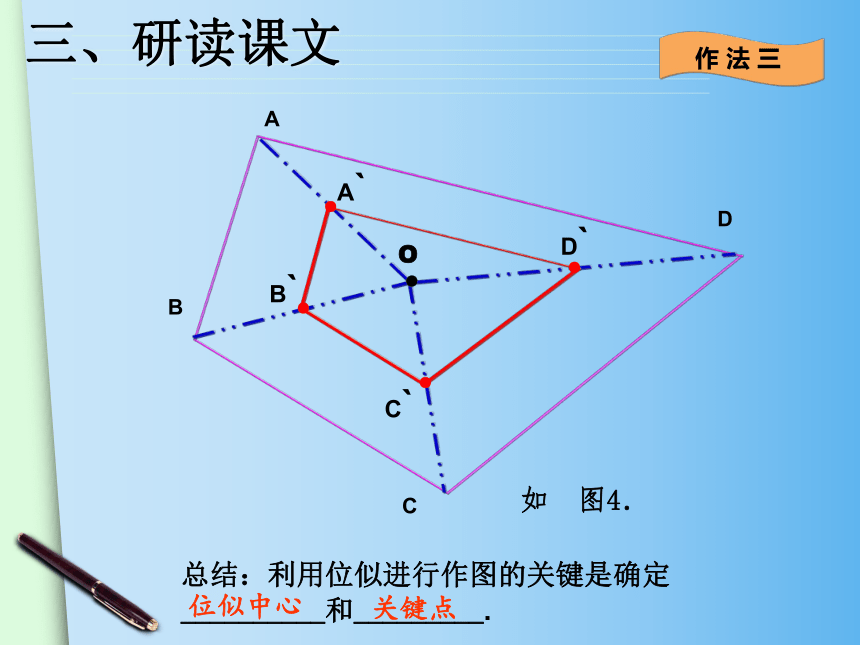
如 图4.
总结:利用位似进行作图的关键是确定 __________和_________.
D
C
B
A
作 法 三
O
A`
B`
C`
D`
●
●
●
●
●
位似中心
关键点
三、研读课文
把右图中的五边形ABCDE扩大到原来的2倍。
练 一 练
O
A`
B`
C`
D`
E`
E
D
C
B
A
●
●
●
●
●
●
四、归纳小结
1、如果两个图形不仅是相似图形,而且是每组对应点连线相交于 ,对应边互相 ,那么这样的两个图形叫做_________.这个点叫做 .
2、利用位似进行作图的关键是确定______ _和
_________.
3、学习反思:______________________ __
__________________________________________________________________ ______ .
一点
平行
位似图形
位似中心
位似中心
关键点
五、强化训练
1、画出所给图中的位似中心.
●
●
●
(红点表示位似中心)
五、强化训练
2、画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A`B`C`D`E`。
E
D
C
O
●
B
A
●
●
●
●
●
A`
B`
D`
C`
E`
五、强化训练
3、已知:如图,△ABC,画△A′B′C′,使△A′B′C′∽△ABC,且使相似比为1.5,
要求:(1)位似中心在△ABC的一条边AB上;
(2)以点C为位似中心.
B
A
C
B
A
B
A
B
A
B
A
五、强化训练
(1)位似中心在△ABC的一条边AB上
B
A
C
B
A
B
A
B
A
B
A
(2)以点C为位似中心
B
A
C
B
A
B
A
B
A
B
A
假设位似中心点O在AB上,
相似比1:5,
点O位置如图(1)所示
o
●
●
A`
B`
C`
●
●
●
A`
B`
(C`)
●
●
第27章相似
27.3 位似(2)
一、新课引入
解: 位似与相似既有联系又有区别,相似只要求两个图形形状完全相同;而位似是在相似的基础上要求对应点的连线相交于一点,且对应边互相平行。
如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形.
因此位似是相似的特殊情况,利用位似,可以把一个图形放大或缩小。
1、位似和相似有什么区别与联系?
一、新课引入
解: 首先确定位似中心,位似中心的位置可随意选择(除非题目指明);
确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
符合要求的图形不惟一,因为所作图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形,最好做两个.
2、作位似图形有哪些步骤?
1
2
3
二、学习目标
巩固位似图形及其有关概念;
会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律;
了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.
三、研读课文
知识点一
认真阅读课本第61至63页的内容,完成下面练习并体验知识点的形成过程.
(1)如图,在平面直角坐标中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把
线段AB缩小.
三、研读课文
知识点一
在第一象限内,将A(6,3),B(6,0)的横坐标、纵坐标缩小后为A ( , )、B ( , ), 连接A B .在第三象限内,将A(6,3),B(6,0)的横坐标、纵坐标缩小后为A"( , )、B"( , ),连接A"B".观察对应点之间坐标的变化,你有什么发现?
2
1
2
0
-2
-1
-2
0
对应点的坐标的比等
于 或 -
三、研读课文
知识点一
(2)如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大.
三、研读课文
知识点一
在第一象限内,将A(2,3),B(2,1),C(6,2)的横坐标,纵坐标分别放大后得到坐标为A ( , )、B ( , )、
C ( , ),连接A B 、B C 、A C .
在第三象限内,将A(2,3),B(2,1),C(6,2),的横坐标,纵坐标分别放大后得到坐标为A"( , )、B"( , )C"( , ),连接A"B"、B" C"、A" C" .
4
6
4
2
12
4
A
B
C
-4
-6
-4
-2
-12
-4
A"
B"
C"
三、研读课文
知识点一
在平面直角坐标系中,如果位似变换是以 为位似中心,相似比为k,那么位似图形对应点的坐标的比等于 或 .
原点
k
-k
不同方法得到的图形坐标是不同的.
三、研读课文
知识点一
△ABC三个顶点坐标分别为A(2,-2),
B(4,-5),C(5,-1),以原点O为位似中心,将这个三角形放大为原来的2倍后得到△DEF.△DEF各个顶点坐标分别为多少?
解:△DEF各个顶点坐标分别为 D(4,-4),E(8,-10),F(10,-2)或D(-4,4),E(-8,10),F(-10,2).
随堂练习
三、研读课文
知识点二
例(教材P62的例题) 如图,在平面直角坐标系中,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出一个以原点O为位似中心,相似比为1:2的位似图形.
三、研读课文
知识点二
问题的关键是要确定位似图形各个顶点的坐标,根据前面的规律,点A的对应点A 的坐标为
(-6× ,6× ),
即(-3,3).类似地,可以确定其他顶点的坐标.
解:如图,利用位似中对应点的坐标的变化规律,分别取点A (-3,3),B (-4,1),C (-2,0),
D (-1,2).依次连接A ,B ,C ,D .四边形A B C D
就是要求的四边形ABCD的位似图形.
A
B
C
D
分析:
三、研读课文
知识点二
问:你能画出几种不同情况的图形呢?
A"
B"
C"
D"
A
B
C
D
解:如图,能画出两种不
同情况的图形.
三、研读课文
知识点二
如图, 三个
顶点坐标分别为
, , ,在网格图中作以点O为位似中心,相似比为2的位似
.位似变换后的对应点坐标为:
A ( ) ,B ( ) ,
C ( ).
4,6
4,2
6,2
A
B
C
四、归纳小结
1、在平面直角坐标系中,如果位似变换是以
为位似中心,相似比为k,那么位似
图形对应点的坐标的比等于 或 .
2、学习反思:______________________
__________________________________
____________________________ .
原点
k
-k
你有什么感悟 与同伴一起分享吧!
五、强化训练
1、△ABO的定点坐标分别为A(-1,4),B(3,2),O(0,0),试将△ABO放大为△EFO,使△EFO与△ABO的相似比为2.5∶1,求点E和点F的坐标.
解:利用位似中对应点的坐标的变化规律,知E(-2.5,10),F(7.5,5).
或E(2.5,-10),F(-7.5,-5).
五、强化训练
2、如下图,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点,以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1︰2.
A
B
C
解:如图,利用位似中对应点的坐标的变化规律,分别取点
A (0,2),B (-1,0),C (2,0).依次连接A ,B ,
C .△A′B′C′就是要求的△ABC的位似图形.
你真棒!
第二十七章 相似
27.3 位似(1)
行 甚 于 言
——清华大学 校训名言
一、新课引入
1、我们学过的图形变换形式有哪些?
2、什么叫相似?相似与全等有什么区别与联系?
平移、旋转、对称
相似:形状相同。
全等:大小、形状相同,能够重合
区别:相似不一定全等,但全等一定相似。
联系:形状相同
1
2
二、学习目标
了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质;
掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
三、研读课文
知识点一
认真阅读课本第59至60页的内容,完成下面练习并体验知识点的形成过程.
1、生活中我们经常把自己好看的照片放大或缩小,由于没有改变图形的形状,我们得到的照片是真实的.
三、研读课文
知识点一
思考 图中多边形相似吗?如果有,那么这种相似有什么特征?
如果两个图形不仅是相似图形,而且是每组对应点连线相交于 ,对应边互相 ,那么这样的两个图形叫做_________.这个点叫做 .(位似中心可在形上、形外、形内.)
位似图形及其有关概念
一点
平行
位似图形
位似中心
三、研读课文
练 一 练
1、下列说法正确的是( )
A. 全等图形一定是位似图形.
B.相似图形一定是位似图形.
C.位似图形一定是全等图形.
D.位似图形是具有某种特殊位置的相似图形.
D
三、研读课文
2、如图,指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心。
是否位似图形 位似中心
图(1)
图(2)
图(3)
图(4)
图(5)
是
点A
是
点P
不是
是
点O
不是
练 一 练
三、研读课文
知识点二
分析:把原图形缩小到原来的 ,也就是使新图形上各顶点到位似中心的距离与原图形各对应顶点到位似中心的距离之比为1∶2 。
例2(教材P60例题) 把图1中的四边形ABCD缩小到
原来的 。
图1
位 似 作 图
D
C
B
A
C
D
B
A
●
●
●
●
●
A`
B`
C`
D`
O
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′、B′、C′、D′,使得
;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′,如图2.
作 法 一
问:此作图题还
有其它作法吗?
三、研读课文
如 图3
作 法 二
D
C
B
A
O
●
●
A`
B`
C`
D`
三、研读课文
●
●
●
三、研读课文
如 图4.
总结:利用位似进行作图的关键是确定 __________和_________.
D
C
B
A
作 法 三
O
A`
B`
C`
D`
●
●
●
●
●
位似中心
关键点
三、研读课文
把右图中的五边形ABCDE扩大到原来的2倍。
练 一 练
O
A`
B`
C`
D`
E`
E
D
C
B
A
●
●
●
●
●
●
四、归纳小结
1、如果两个图形不仅是相似图形,而且是每组对应点连线相交于 ,对应边互相 ,那么这样的两个图形叫做_________.这个点叫做 .
2、利用位似进行作图的关键是确定______ _和
_________.
3、学习反思:______________________ __
__________________________________________________________________ ______ .
一点
平行
位似图形
位似中心
位似中心
关键点
五、强化训练
1、画出所给图中的位似中心.
●
●
●
(红点表示位似中心)
五、强化训练
2、画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A`B`C`D`E`。
E
D
C
O
●
B
A
●
●
●
●
●
A`
B`
D`
C`
E`
五、强化训练
3、已知:如图,△ABC,画△A′B′C′,使△A′B′C′∽△ABC,且使相似比为1.5,
要求:(1)位似中心在△ABC的一条边AB上;
(2)以点C为位似中心.
B
A
C
B
A
B
A
B
A
B
A
五、强化训练
(1)位似中心在△ABC的一条边AB上
B
A
C
B
A
B
A
B
A
B
A
(2)以点C为位似中心
B
A
C
B
A
B
A
B
A
B
A
假设位似中心点O在AB上,
相似比1:5,
点O位置如图(1)所示
o
●
●
A`
B`
C`
●
●
●
A`
B`
(C`)
●
●
第27章相似
27.3 位似(2)
一、新课引入
解: 位似与相似既有联系又有区别,相似只要求两个图形形状完全相同;而位似是在相似的基础上要求对应点的连线相交于一点,且对应边互相平行。
如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形.
因此位似是相似的特殊情况,利用位似,可以把一个图形放大或缩小。
1、位似和相似有什么区别与联系?
一、新课引入
解: 首先确定位似中心,位似中心的位置可随意选择(除非题目指明);
确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
符合要求的图形不惟一,因为所作图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形,最好做两个.
2、作位似图形有哪些步骤?
1
2
3
二、学习目标
巩固位似图形及其有关概念;
会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律;
了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.
三、研读课文
知识点一
认真阅读课本第61至63页的内容,完成下面练习并体验知识点的形成过程.
(1)如图,在平面直角坐标中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把
线段AB缩小.
三、研读课文
知识点一
在第一象限内,将A(6,3),B(6,0)的横坐标、纵坐标缩小后为A ( , )、B ( , ), 连接A B .在第三象限内,将A(6,3),B(6,0)的横坐标、纵坐标缩小后为A"( , )、B"( , ),连接A"B".观察对应点之间坐标的变化,你有什么发现?
2
1
2
0
-2
-1
-2
0
对应点的坐标的比等
于 或 -
三、研读课文
知识点一
(2)如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大.
三、研读课文
知识点一
在第一象限内,将A(2,3),B(2,1),C(6,2)的横坐标,纵坐标分别放大后得到坐标为A ( , )、B ( , )、
C ( , ),连接A B 、B C 、A C .
在第三象限内,将A(2,3),B(2,1),C(6,2),的横坐标,纵坐标分别放大后得到坐标为A"( , )、B"( , )C"( , ),连接A"B"、B" C"、A" C" .
4
6
4
2
12
4
A
B
C
-4
-6
-4
-2
-12
-4
A"
B"
C"
三、研读课文
知识点一
在平面直角坐标系中,如果位似变换是以 为位似中心,相似比为k,那么位似图形对应点的坐标的比等于 或 .
原点
k
-k
不同方法得到的图形坐标是不同的.
三、研读课文
知识点一
△ABC三个顶点坐标分别为A(2,-2),
B(4,-5),C(5,-1),以原点O为位似中心,将这个三角形放大为原来的2倍后得到△DEF.△DEF各个顶点坐标分别为多少?
解:△DEF各个顶点坐标分别为 D(4,-4),E(8,-10),F(10,-2)或D(-4,4),E(-8,10),F(-10,2).
随堂练习
三、研读课文
知识点二
例(教材P62的例题) 如图,在平面直角坐标系中,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出一个以原点O为位似中心,相似比为1:2的位似图形.
三、研读课文
知识点二
问题的关键是要确定位似图形各个顶点的坐标,根据前面的规律,点A的对应点A 的坐标为
(-6× ,6× ),
即(-3,3).类似地,可以确定其他顶点的坐标.
解:如图,利用位似中对应点的坐标的变化规律,分别取点A (-3,3),B (-4,1),C (-2,0),
D (-1,2).依次连接A ,B ,C ,D .四边形A B C D
就是要求的四边形ABCD的位似图形.
A
B
C
D
分析:
三、研读课文
知识点二
问:你能画出几种不同情况的图形呢?
A"
B"
C"
D"
A
B
C
D
解:如图,能画出两种不
同情况的图形.
三、研读课文
知识点二
如图, 三个
顶点坐标分别为
, , ,在网格图中作以点O为位似中心,相似比为2的位似
.位似变换后的对应点坐标为:
A ( ) ,B ( ) ,
C ( ).
4,6
4,2
6,2
A
B
C
四、归纳小结
1、在平面直角坐标系中,如果位似变换是以
为位似中心,相似比为k,那么位似
图形对应点的坐标的比等于 或 .
2、学习反思:______________________
__________________________________
____________________________ .
原点
k
-k
你有什么感悟 与同伴一起分享吧!
五、强化训练
1、△ABO的定点坐标分别为A(-1,4),B(3,2),O(0,0),试将△ABO放大为△EFO,使△EFO与△ABO的相似比为2.5∶1,求点E和点F的坐标.
解:利用位似中对应点的坐标的变化规律,知E(-2.5,10),F(7.5,5).
或E(2.5,-10),F(-7.5,-5).
五、强化训练
2、如下图,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点,以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1︰2.
A
B
C
解:如图,利用位似中对应点的坐标的变化规律,分别取点
A (0,2),B (-1,0),C (2,0).依次连接A ,B ,
C .△A′B′C′就是要求的△ABC的位似图形.
你真棒!
