【备考2022】泰安市近十年中考数学 考点18 函数的概念、图象与性质(含答案)
文档属性
| 名称 | 【备考2022】泰安市近十年中考数学 考点18 函数的概念、图象与性质(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 545.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 16:57:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
十八、 函数的概念、图象与性质
[基础知识]
一次函数、反比例函数、二次函数的一般形式 ;
一次函数中系数k、b与图象位置的关系、函数的增减性 ;
反比例函数中系数k与图象位置的关系、函数的增减性;
二次函数中系数a、b、c与图象位置的关系、函数的增减性。
①二次函数的a决定抛物线的开口方向和开口大小②抛物线对称轴的位置决定a、b的符号③二次函数的c决定抛物线与Y轴交点的位置④ 当x取特殊值1、-1、2-、-2等时对应代数式的值⑤二次函数的增减性⑥自变量x取不同值,所对应的y值的大小比较
二次函数的对称轴、顶点坐标。
函数与方程、不等式的关系。
分段函数(自变量取值范围)的确定。
[中考真题]
(2021)8.(4分)将抛物线y=﹣x2﹣2x+3的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A.(﹣2,2) B.(﹣1,1) C.(0,6) D.(1,﹣3)
(2021)15.(3分)如图是抛物线y=ax2+bx+c的部分图象,图象过点(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②a﹣b+c=0;③y的最大值为3;④方程ax2+bx+c+1=0有实数根.其中正确的为 (将所有正确结论的序号都填入).
(2020)9.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
(2020)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:则下列结论:
①a>0;
②当x=﹣2时,函数最小值为﹣6;
③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;
④方程ax2+bx+c=﹣5有两个不相等的实数根.
其中,正确结论的序号是 .(把所有正确结论的序号都填上)
(2019)16.(4分)若二次函数y=x2+bx﹣5的对称轴为直线x=2,则关于x的方程x2+bx﹣5=2x﹣13的解为 .
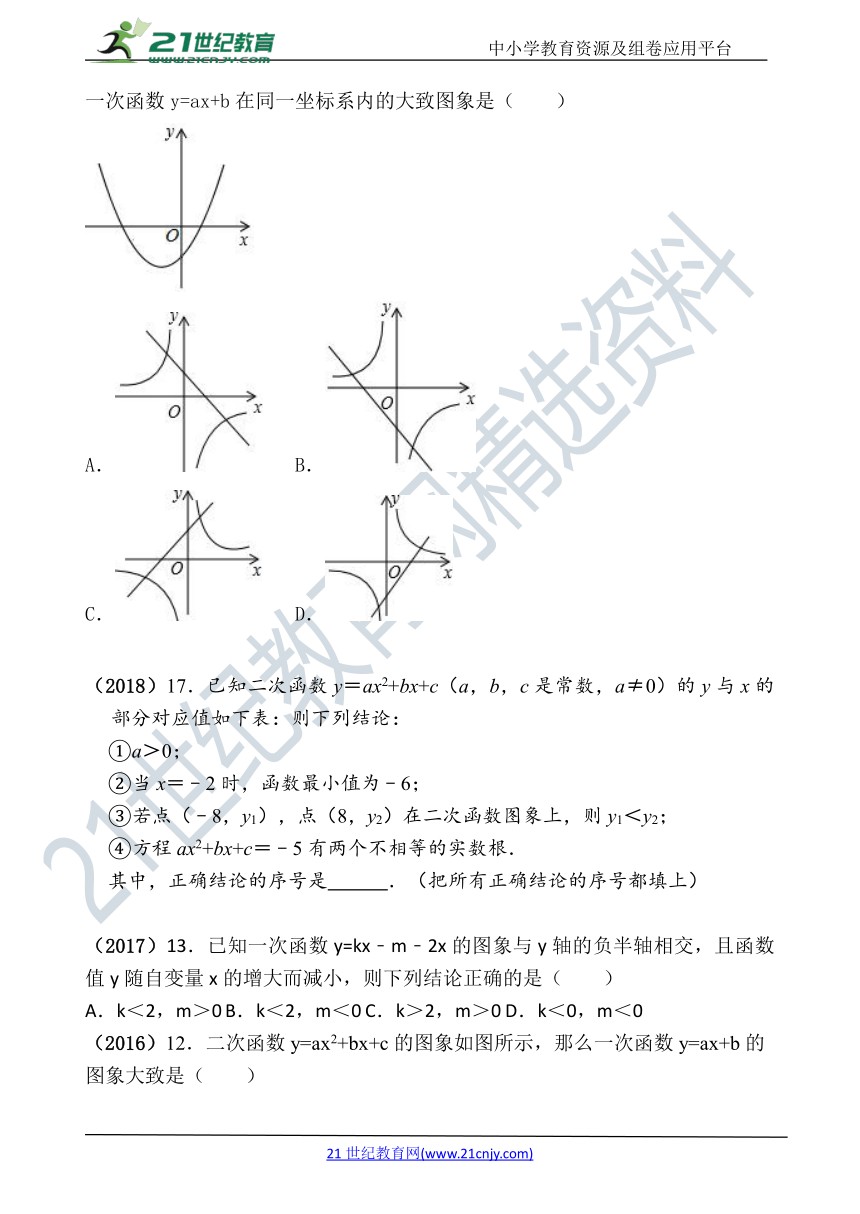
(2018)7.(3分) 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=ax+b在同一坐标系内的大致图象是( )
B.
C. D.
(2018)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:则下列结论:
①a>0;
②当x=﹣2时,函数最小值为﹣6;
③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;
④方程ax2+bx+c=﹣5有两个不相等的实数根.
其中,正确结论的序号是 .(把所有正确结论的序号都填上)
(2017)13.已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 D.k<0,m<0
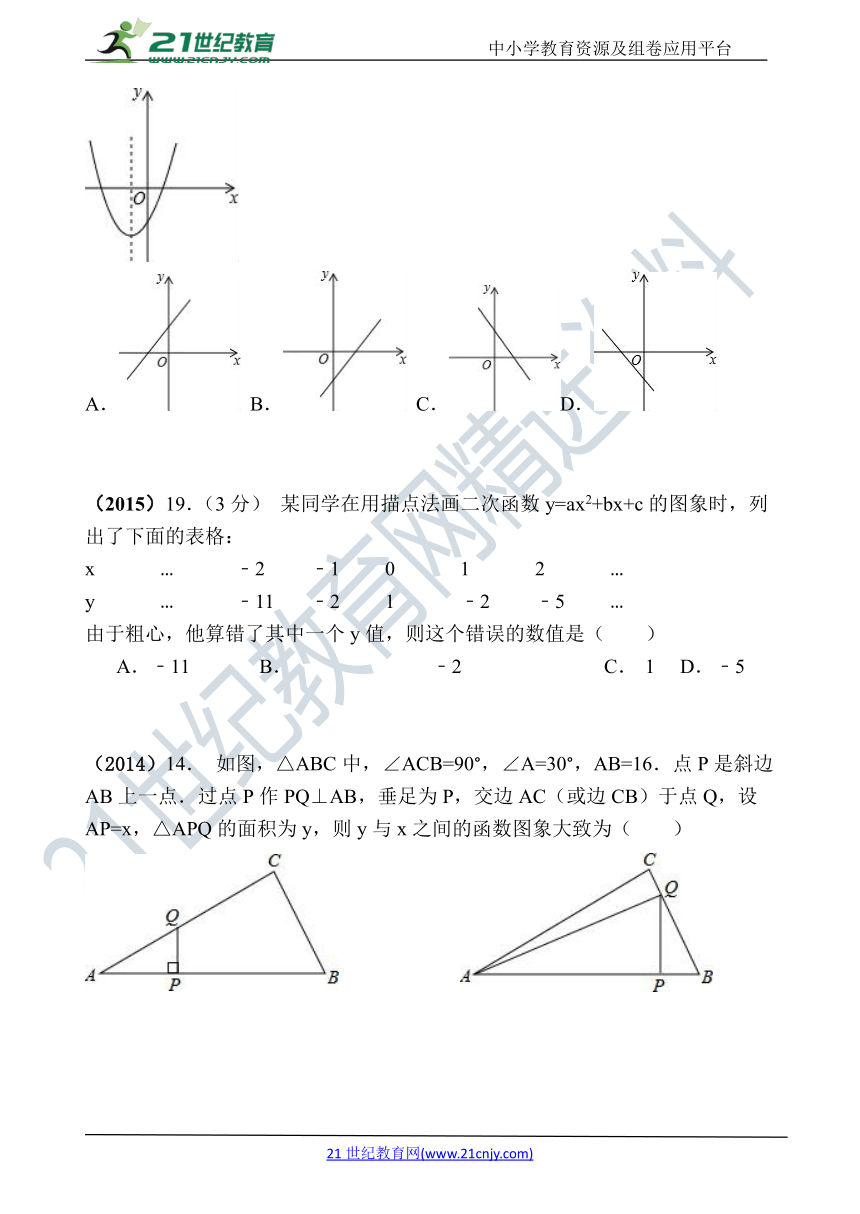
(2016)12.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
B. C.D.
(2015)19.(3分) 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 2 …
y … ﹣11 ﹣2 1 ﹣2 ﹣5 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣11 B. ﹣2 C. 1 D. ﹣5
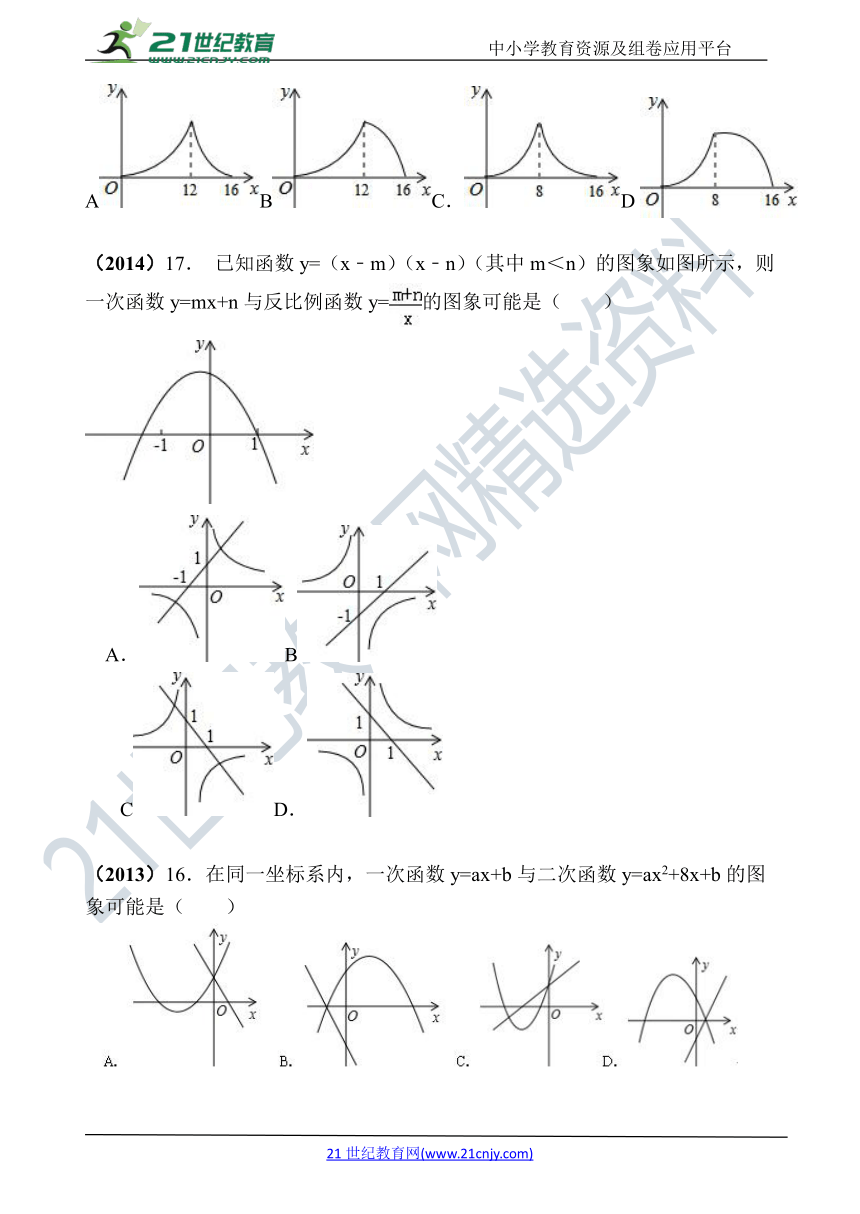
(2014)14. 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
ABC.D
(2014)17. 已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B CD.
(2013)16.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
(2013)17.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
(2012)10.(2012泰安)二次函数的图象如图,若一元二次方程有实数根,则 的最大值为( )
A. B.3 C. D.9
(2012)12.(2012泰安)将抛物线向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
B.
C. D.
(2012)16.二次函数的图象如图,则一次函数的图象经过( )
第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
(2012)19. 设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
[答案解析]
(2021)8.(4分)将抛物线y=﹣x2﹣2x+3的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A.(﹣2,2) B.(﹣1,1) C.(0,6) D.(1,﹣3)
【分析】利用函数的概念,自变量和应变量的关系解决问题。
【解答】:y=﹣x2﹣2x+3
=﹣(x2+2x)+3
=﹣[(x+1)2﹣1]+3
=﹣(x+1)2+4,
∵将抛物线y=﹣x2﹣2x+3的图象向右平移1个单位,再向下平移2个单位,
∴得到的抛物线解析式为:y=﹣x2+2,
当x=﹣2时,y=﹣(﹣2)2+2=﹣4+2=﹣2,故(﹣2,2)不在此抛物线上,故A选项不合题意;
当x=﹣1时,y=﹣(﹣1)2+2=﹣1+2=1,故(﹣1,1)在此抛物线上,故B选项符合题意;
当x=0时,y=﹣02+2=0+2=2,故(0,6)不在此抛物线上,故A选项不合题意;
当x=1时,y=﹣12+2=﹣1+2=1,故(1,﹣3)不在此抛物线上,故A选项不合题意;
故选:B.
(2021)15.(3分)如图是抛物线y=ax2+bx+c的部分图象,图象过点(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②a﹣b+c=0;③y的最大值为3;④方程ax2+bx+c+1=0有实数根.其中正确的为 (将所有正确结论的序号都填入).
【分析】根据函数图象与系数的关系解答问题。
【解答】:∵抛物线开口向下,
∴a<0,
∵对称轴x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴的交点在y轴正半轴,
∴c>0,
∴abc<0,故①错误;
∵抛物线与x轴的交点(3,0),对称轴为直线x=1,
∴抛物线x轴的另一个交点在(﹣1,0),
∴当x=﹣1时,y=a﹣b+c=0,即②正确;
由图象无法判断y的最大值,故③错误;
方程ax2+bx+c+1=0,可看作二次函数y=ax2+bx+c与y=﹣1的交点个数,
由图象可知,必然有2个交点,即方程ax2+bx+c+1=0有2个不想等的实数根.
故④正确.
故答案为:②④.
(2020)9.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
【分析】根据二次函数图象的开口以及对称轴与y轴的关系即可得出a、b的正负,由此即可得出一次函数图象经过的象限,再与函数图象进行对比即可得出结论.
【解答】:A、二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,
故A错误;
B、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,且与二次函数交于y轴负半轴的同一点,
故B错误;
C、二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,
故C正确;
∵D、二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,
故D错误;
故选:C.
x ﹣5 ﹣4 ﹣2 0 2
y 6 0 ﹣6 ﹣4 6
(2020)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:则下列结论:
①a>0;
②当x=﹣2时,函数最小值为﹣6;
③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;
④方程ax2+bx+c=﹣5有两个不相等的实数根.
其中,正确结论的序号是 .(把所有正确结论的序号都填上)
【分析】任意取表格中的三组对应值,求出二次函数的关系式,再根据二次函数的图象与系数之间的关系进行判断即可.
【解答】:将(﹣4,0)(0,﹣4)(2,6)代入y=ax2+bx+c得,
,解得,,
∴抛物线的关系式为y=x2+3x﹣4,
a=1>0,因此①正确;
对称轴为x=﹣,即当x=﹣时,函数的值最小,因此②不正确;
把(﹣8,y1)(8,y2)代入关系式得,y1=64﹣24﹣4=36,y2=64+24﹣4=84,因此③正确;
方程ax2+bx+c=﹣5,也就是x2+3x﹣4=﹣5,即方x2+3x+1=0,由b2﹣4ac=9﹣4=5>0可得x2+3x+1=0有两个不相等的实数根,因此④正确;
正确的结论有:①③④,
故答案为:①③④.
(2019)16.(4分)若二次函数y=x2+bx﹣5的对称轴为直线x=2,则关于x的方程x2+bx﹣5=2x﹣13的解为 .
【分析】根据对称轴方程求得b,再解一元二次方程得解.
【解答】:∵二次函数y=x2+bx﹣5的对称轴为直线x=2,
∴,
得b=﹣4,
则x2+bx﹣5=2x﹣13可化为:x2﹣4x﹣5=2x﹣13,
解得,x1=2,x2=4.
故意答案为:x1=2,x2=4.
【总结】本题主要考查的是抛物线与x轴的交点,利用抛物线的对称性求得b的值是解题的关键.
(2018)7.(3分) 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=ax+b在同一坐标系内的大致图象是( )
B.
C. D.
【分析】 首先利用二次函数图象得出a,b的值,进而结合反比例函数以及一次函数的性质得出答案.
【解答】:由二次函数开口向上可得:a>0,对称轴在y轴左侧,故a,b同号,则b>0,
故反比例函数y=图象分布在第一、三象限,一次函数y=ax+b经过第一、二、三象限.
故选:C.
【总结】此题主要考查了二次函数、一次函数、反比例函数的图象,正确得出a,b的值是解题关键.
(2017)13.已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 D.k<0,m<0
【分析】由一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交且函数值y随自变量x的增大而减小,可得出k﹣2<0、﹣m<0,解之即可得出结论.
【解答】:∵一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,
∴k﹣2<0,﹣m<0,
∴k<2,m>0.
故选A.
(2016)12.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
B. C.D.
【分析】由y=ax2+bx+c的图象判断出a>0,b<0,于是得到一次函数y=ax+b的图象经过一,二,四象限,即可得到结论.
【解答】:∵y=ax2+bx+c的图象的开口向上,
∴a>0,
∵对称轴在y轴的左侧,
∴b>0,
∴一次函数y=ax+b的图象经过一,二,三象限.
故选A.
【总结】本题考查了二次函数和一次函数的图象,解题的关键是明确二次函数的性质,由函数图象可以判断a、b的取值范围.
(2015)19.(3分) 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 2 …
y … ﹣11 ﹣2 1 ﹣2 ﹣5 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣11 B. ﹣2 C. 1 D. ﹣5
【分析】根据关于对称轴对称的自变量对应的函数值相等,可得答案.
【解答】:由函数图象关于对称轴对称,得
(﹣1,﹣2),(0,1),(1,2)在函数图象上,
把(﹣1,﹣2),(0,1),(1,﹣2)代入函数解析式,得
,
解得,
函数解析式为y=﹣3x2+1
x=2时y=﹣11,
故选:D.
【总结】本题考查了二次函数图象,利用函数图象关于对称轴对称是解题关键.
:
(2014)14. 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
ABC.D
【分析】分点Q在AC上和BC上两种情况进行讨论即可.
【解答】当点Q在AC上时,∵∠A=30°,AP=x,∴PQ=xtan30°= ∴y=×AP×PQ=×x×=x2;
当点Q在BC上时,如图所示:
∵AP=x,AB=16,∠A=30°,∴BP=16﹣x,∠B=60°,
∴PQ=BP tan60°=(16﹣x).
∴==.
∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.
故选:B.
【总结】本题考查动点问题的函数图象,有一定难度,解题关键是注意点Q在BC上这种情况.
(2014)17. 已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B CD.
【分析】根据二次函数图象判断出m<﹣1,n=1,然后求出m+n<0,再根据一次函数与反比例函数图象的性质判断即可.
【解答】:由图可知,m<﹣1,n=1,所以,m+n<0,
所以,一次函数y=mx+n经过第二四象限,且与y轴相交于点(0,1),
反比例函数y=的图象位于第二四象限,
纵观各选项,只有C选项图形符合.故选C.
【总结】本题考查了二次函数图象,一次函数图象,反比例函数图象,观察二次函数图象判断出m、n的取值是解题的关键.
(2013)16.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
【分析】令x=0,求出两个函数图象在y轴上相交于同一点,再根据抛物线开口方向向上确定出a>0,然后确定出一次函数图象经过第一三象限,从而得解.
【解答】:x=0时,两个函数的函数值y=b,
所以,两个函数图象与y轴相交于同一点,故B、D选项错误;
由A、C选项可知,抛物线开口方向向上,
所以,a>0,
所以,一次函数y=ax+b经过第一三象限,
所以,A选项错误,C选项正确.
故选C.
【总结】本题考查了二次函数图象,一次函数的图象,应该熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.
(2013)17.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
【分析】直线y=﹣x+3向上平移m个单位后可得:y=﹣x+3+m,求出直线y=﹣x+3+m与直线y=2x+4的交点,再由此点在第一象限可得出m的取值范围.
【解答】:直线y=﹣x+3向上平移m个单位后可得:y=﹣x+3+m,
联立两直线解析式得:,
解得:,
即交点坐标为(,),
∵交点在第一象限,
∴,
解得:m>1.
故选C.
【总结】本题考查了一次函数图象与几何变换、两直线的交点坐标,注意第一象限的点的横、纵坐标均大于0.
(2012)10.(2012泰安)二次函数的图象如图,若一元二次方程有实数根,则 的最大值为( )
A. B.3 C. D.9
【分析】抛物线与x轴的交点。
【解答】:∵抛物线的开口向上,顶点纵坐标为﹣3,
∴a>0.,即,
∵一元二次方程有实数根,
∴△=,即,即,解得,
∴m的最大值为3.
故选B.
(2012)12.(2012泰安)将抛物线向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A. B. C. D.
【分析】二次函数图象与几何变换。
【解答】:由“上加下减”的原则可知,将抛物线向上平移3个单位所得抛物线的解析式为:;
由“左加右减”的原则可知,将抛物线向左平移2个单位所得抛物线的解析式为:.
故选A.
(2012)16.二次函数的图象如图,则一次函数的图象经过( )
A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限
【分析】二次函数的图象;一次函数的性质。
【解答】:∵抛物线的顶点在第四象限,
∴﹣m>0,n<0,
∴m<0,
∴一次函数的图象经过二、三、四象限,
故选C.
(2012)19. 设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
【分析】二次函数图象上点的坐标特征。
【解答】:∵函数的解析式是,如右图,
∴对称轴是,
∴点A关于对称轴的点A′是(0,y1),
那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小,
于是.
故选A.
[解题攻略]
明确函数的性质,由函数图象可以判断系数的取值范围是解本类题目的关键.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
十八、 函数的概念、图象与性质
[基础知识]
一次函数、反比例函数、二次函数的一般形式 ;
一次函数中系数k、b与图象位置的关系、函数的增减性 ;
反比例函数中系数k与图象位置的关系、函数的增减性;
二次函数中系数a、b、c与图象位置的关系、函数的增减性。
①二次函数的a决定抛物线的开口方向和开口大小②抛物线对称轴的位置决定a、b的符号③二次函数的c决定抛物线与Y轴交点的位置④ 当x取特殊值1、-1、2-、-2等时对应代数式的值⑤二次函数的增减性⑥自变量x取不同值,所对应的y值的大小比较
二次函数的对称轴、顶点坐标。
函数与方程、不等式的关系。
分段函数(自变量取值范围)的确定。
[中考真题]
(2021)8.(4分)将抛物线y=﹣x2﹣2x+3的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A.(﹣2,2) B.(﹣1,1) C.(0,6) D.(1,﹣3)
(2021)15.(3分)如图是抛物线y=ax2+bx+c的部分图象,图象过点(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②a﹣b+c=0;③y的最大值为3;④方程ax2+bx+c+1=0有实数根.其中正确的为 (将所有正确结论的序号都填入).
(2020)9.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
(2020)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:则下列结论:
①a>0;
②当x=﹣2时,函数最小值为﹣6;
③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;
④方程ax2+bx+c=﹣5有两个不相等的实数根.
其中,正确结论的序号是 .(把所有正确结论的序号都填上)
(2019)16.(4分)若二次函数y=x2+bx﹣5的对称轴为直线x=2,则关于x的方程x2+bx﹣5=2x﹣13的解为 .
(2018)7.(3分) 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=ax+b在同一坐标系内的大致图象是( )
B.
C. D.
(2018)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:则下列结论:
①a>0;
②当x=﹣2时,函数最小值为﹣6;
③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;
④方程ax2+bx+c=﹣5有两个不相等的实数根.
其中,正确结论的序号是 .(把所有正确结论的序号都填上)
(2017)13.已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 D.k<0,m<0
(2016)12.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
B. C.D.
(2015)19.(3分) 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 2 …
y … ﹣11 ﹣2 1 ﹣2 ﹣5 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣11 B. ﹣2 C. 1 D. ﹣5
(2014)14. 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
ABC.D
(2014)17. 已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B CD.
(2013)16.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
(2013)17.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
(2012)10.(2012泰安)二次函数的图象如图,若一元二次方程有实数根,则 的最大值为( )
A. B.3 C. D.9
(2012)12.(2012泰安)将抛物线向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
B.
C. D.
(2012)16.二次函数的图象如图,则一次函数的图象经过( )
第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
(2012)19. 设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
[答案解析]
(2021)8.(4分)将抛物线y=﹣x2﹣2x+3的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A.(﹣2,2) B.(﹣1,1) C.(0,6) D.(1,﹣3)
【分析】利用函数的概念,自变量和应变量的关系解决问题。
【解答】:y=﹣x2﹣2x+3
=﹣(x2+2x)+3
=﹣[(x+1)2﹣1]+3
=﹣(x+1)2+4,
∵将抛物线y=﹣x2﹣2x+3的图象向右平移1个单位,再向下平移2个单位,
∴得到的抛物线解析式为:y=﹣x2+2,
当x=﹣2时,y=﹣(﹣2)2+2=﹣4+2=﹣2,故(﹣2,2)不在此抛物线上,故A选项不合题意;
当x=﹣1时,y=﹣(﹣1)2+2=﹣1+2=1,故(﹣1,1)在此抛物线上,故B选项符合题意;
当x=0时,y=﹣02+2=0+2=2,故(0,6)不在此抛物线上,故A选项不合题意;
当x=1时,y=﹣12+2=﹣1+2=1,故(1,﹣3)不在此抛物线上,故A选项不合题意;
故选:B.
(2021)15.(3分)如图是抛物线y=ax2+bx+c的部分图象,图象过点(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②a﹣b+c=0;③y的最大值为3;④方程ax2+bx+c+1=0有实数根.其中正确的为 (将所有正确结论的序号都填入).
【分析】根据函数图象与系数的关系解答问题。
【解答】:∵抛物线开口向下,
∴a<0,
∵对称轴x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴的交点在y轴正半轴,
∴c>0,
∴abc<0,故①错误;
∵抛物线与x轴的交点(3,0),对称轴为直线x=1,
∴抛物线x轴的另一个交点在(﹣1,0),
∴当x=﹣1时,y=a﹣b+c=0,即②正确;
由图象无法判断y的最大值,故③错误;
方程ax2+bx+c+1=0,可看作二次函数y=ax2+bx+c与y=﹣1的交点个数,
由图象可知,必然有2个交点,即方程ax2+bx+c+1=0有2个不想等的实数根.
故④正确.
故答案为:②④.
(2020)9.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
【分析】根据二次函数图象的开口以及对称轴与y轴的关系即可得出a、b的正负,由此即可得出一次函数图象经过的象限,再与函数图象进行对比即可得出结论.
【解答】:A、二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,
故A错误;
B、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,且与二次函数交于y轴负半轴的同一点,
故B错误;
C、二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,
故C正确;
∵D、二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,
故D错误;
故选:C.
x ﹣5 ﹣4 ﹣2 0 2
y 6 0 ﹣6 ﹣4 6
(2020)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:则下列结论:
①a>0;
②当x=﹣2时,函数最小值为﹣6;
③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;
④方程ax2+bx+c=﹣5有两个不相等的实数根.
其中,正确结论的序号是 .(把所有正确结论的序号都填上)
【分析】任意取表格中的三组对应值,求出二次函数的关系式,再根据二次函数的图象与系数之间的关系进行判断即可.
【解答】:将(﹣4,0)(0,﹣4)(2,6)代入y=ax2+bx+c得,
,解得,,
∴抛物线的关系式为y=x2+3x﹣4,
a=1>0,因此①正确;
对称轴为x=﹣,即当x=﹣时,函数的值最小,因此②不正确;
把(﹣8,y1)(8,y2)代入关系式得,y1=64﹣24﹣4=36,y2=64+24﹣4=84,因此③正确;
方程ax2+bx+c=﹣5,也就是x2+3x﹣4=﹣5,即方x2+3x+1=0,由b2﹣4ac=9﹣4=5>0可得x2+3x+1=0有两个不相等的实数根,因此④正确;
正确的结论有:①③④,
故答案为:①③④.
(2019)16.(4分)若二次函数y=x2+bx﹣5的对称轴为直线x=2,则关于x的方程x2+bx﹣5=2x﹣13的解为 .
【分析】根据对称轴方程求得b,再解一元二次方程得解.
【解答】:∵二次函数y=x2+bx﹣5的对称轴为直线x=2,
∴,
得b=﹣4,
则x2+bx﹣5=2x﹣13可化为:x2﹣4x﹣5=2x﹣13,
解得,x1=2,x2=4.
故意答案为:x1=2,x2=4.
【总结】本题主要考查的是抛物线与x轴的交点,利用抛物线的对称性求得b的值是解题的关键.
(2018)7.(3分) 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=ax+b在同一坐标系内的大致图象是( )
B.
C. D.
【分析】 首先利用二次函数图象得出a,b的值,进而结合反比例函数以及一次函数的性质得出答案.
【解答】:由二次函数开口向上可得:a>0,对称轴在y轴左侧,故a,b同号,则b>0,
故反比例函数y=图象分布在第一、三象限,一次函数y=ax+b经过第一、二、三象限.
故选:C.
【总结】此题主要考查了二次函数、一次函数、反比例函数的图象,正确得出a,b的值是解题关键.
(2017)13.已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 D.k<0,m<0
【分析】由一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交且函数值y随自变量x的增大而减小,可得出k﹣2<0、﹣m<0,解之即可得出结论.
【解答】:∵一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,
∴k﹣2<0,﹣m<0,
∴k<2,m>0.
故选A.
(2016)12.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
B. C.D.
【分析】由y=ax2+bx+c的图象判断出a>0,b<0,于是得到一次函数y=ax+b的图象经过一,二,四象限,即可得到结论.
【解答】:∵y=ax2+bx+c的图象的开口向上,
∴a>0,
∵对称轴在y轴的左侧,
∴b>0,
∴一次函数y=ax+b的图象经过一,二,三象限.
故选A.
【总结】本题考查了二次函数和一次函数的图象,解题的关键是明确二次函数的性质,由函数图象可以判断a、b的取值范围.
(2015)19.(3分) 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 2 …
y … ﹣11 ﹣2 1 ﹣2 ﹣5 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣11 B. ﹣2 C. 1 D. ﹣5
【分析】根据关于对称轴对称的自变量对应的函数值相等,可得答案.
【解答】:由函数图象关于对称轴对称,得
(﹣1,﹣2),(0,1),(1,2)在函数图象上,
把(﹣1,﹣2),(0,1),(1,﹣2)代入函数解析式,得
,
解得,
函数解析式为y=﹣3x2+1
x=2时y=﹣11,
故选:D.
【总结】本题考查了二次函数图象,利用函数图象关于对称轴对称是解题关键.
:
(2014)14. 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
ABC.D
【分析】分点Q在AC上和BC上两种情况进行讨论即可.
【解答】当点Q在AC上时,∵∠A=30°,AP=x,∴PQ=xtan30°= ∴y=×AP×PQ=×x×=x2;
当点Q在BC上时,如图所示:
∵AP=x,AB=16,∠A=30°,∴BP=16﹣x,∠B=60°,
∴PQ=BP tan60°=(16﹣x).
∴==.
∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.
故选:B.
【总结】本题考查动点问题的函数图象,有一定难度,解题关键是注意点Q在BC上这种情况.
(2014)17. 已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B CD.
【分析】根据二次函数图象判断出m<﹣1,n=1,然后求出m+n<0,再根据一次函数与反比例函数图象的性质判断即可.
【解答】:由图可知,m<﹣1,n=1,所以,m+n<0,
所以,一次函数y=mx+n经过第二四象限,且与y轴相交于点(0,1),
反比例函数y=的图象位于第二四象限,
纵观各选项,只有C选项图形符合.故选C.
【总结】本题考查了二次函数图象,一次函数图象,反比例函数图象,观察二次函数图象判断出m、n的取值是解题的关键.
(2013)16.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
【分析】令x=0,求出两个函数图象在y轴上相交于同一点,再根据抛物线开口方向向上确定出a>0,然后确定出一次函数图象经过第一三象限,从而得解.
【解答】:x=0时,两个函数的函数值y=b,
所以,两个函数图象与y轴相交于同一点,故B、D选项错误;
由A、C选项可知,抛物线开口方向向上,
所以,a>0,
所以,一次函数y=ax+b经过第一三象限,
所以,A选项错误,C选项正确.
故选C.
【总结】本题考查了二次函数图象,一次函数的图象,应该熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.
(2013)17.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
【分析】直线y=﹣x+3向上平移m个单位后可得:y=﹣x+3+m,求出直线y=﹣x+3+m与直线y=2x+4的交点,再由此点在第一象限可得出m的取值范围.
【解答】:直线y=﹣x+3向上平移m个单位后可得:y=﹣x+3+m,
联立两直线解析式得:,
解得:,
即交点坐标为(,),
∵交点在第一象限,
∴,
解得:m>1.
故选C.
【总结】本题考查了一次函数图象与几何变换、两直线的交点坐标,注意第一象限的点的横、纵坐标均大于0.
(2012)10.(2012泰安)二次函数的图象如图,若一元二次方程有实数根,则 的最大值为( )
A. B.3 C. D.9
【分析】抛物线与x轴的交点。
【解答】:∵抛物线的开口向上,顶点纵坐标为﹣3,
∴a>0.,即,
∵一元二次方程有实数根,
∴△=,即,即,解得,
∴m的最大值为3.
故选B.
(2012)12.(2012泰安)将抛物线向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A. B. C. D.
【分析】二次函数图象与几何变换。
【解答】:由“上加下减”的原则可知,将抛物线向上平移3个单位所得抛物线的解析式为:;
由“左加右减”的原则可知,将抛物线向左平移2个单位所得抛物线的解析式为:.
故选A.
(2012)16.二次函数的图象如图,则一次函数的图象经过( )
A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限
【分析】二次函数的图象;一次函数的性质。
【解答】:∵抛物线的顶点在第四象限,
∴﹣m>0,n<0,
∴m<0,
∴一次函数的图象经过二、三、四象限,
故选C.
(2012)19. 设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
【分析】二次函数图象上点的坐标特征。
【解答】:∵函数的解析式是,如右图,
∴对称轴是,
∴点A关于对称轴的点A′是(0,y1),
那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小,
于是.
故选A.
[解题攻略]
明确函数的性质,由函数图象可以判断系数的取值范围是解本类题目的关键.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
