2021-2022学年人教版七年级数学下册5.4平移同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.4平移同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 193.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 12:13:41 | ||
图片预览

文档简介
5.4平移
一、单选题
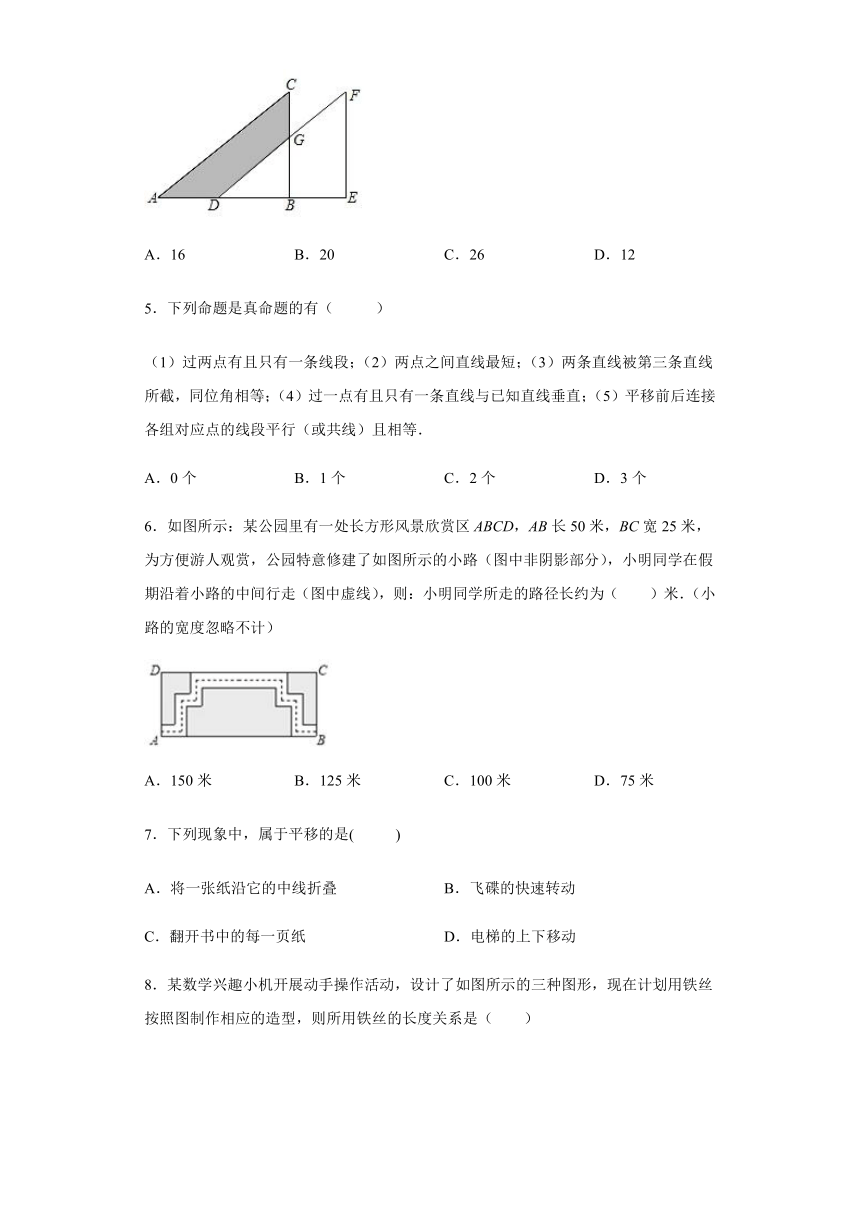
1.下列图形中,把三角形ABC平移后能得到三角形DEF的是( )
2.如图,在7×7的方格纸中,每个小方格都是边长为1的小正方形,网格线的交点称格点,点A,点B是方格纸中的两个格点,找出格点C,使△ABC的面积为3,则满足条件的格点C的个数是( )
A.4个 B.5个 C.6个 D.8个
3.如图所示,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米40元,且知主楼梯道的宽为,其侧面如图所示,则买地毯至少需要( )元.
A.1881.6 B.768 C.1008 D.672
4.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=4,EF=8,CG=3,则图中阴影部分的面积为( )
A.16 B.20 C.26 D.12
5.下列命题是真命题的有( )
(1)过两点有且只有一条线段;(2)两点之间直线最短;(3)两条直线被第三条直线所截,同位角相等;(4)过一点有且只有一条直线与已知直线垂直;(5)平移前后连接各组对应点的线段平行(或共线)且相等.
A.0个 B.1个 C.2个 D.3个
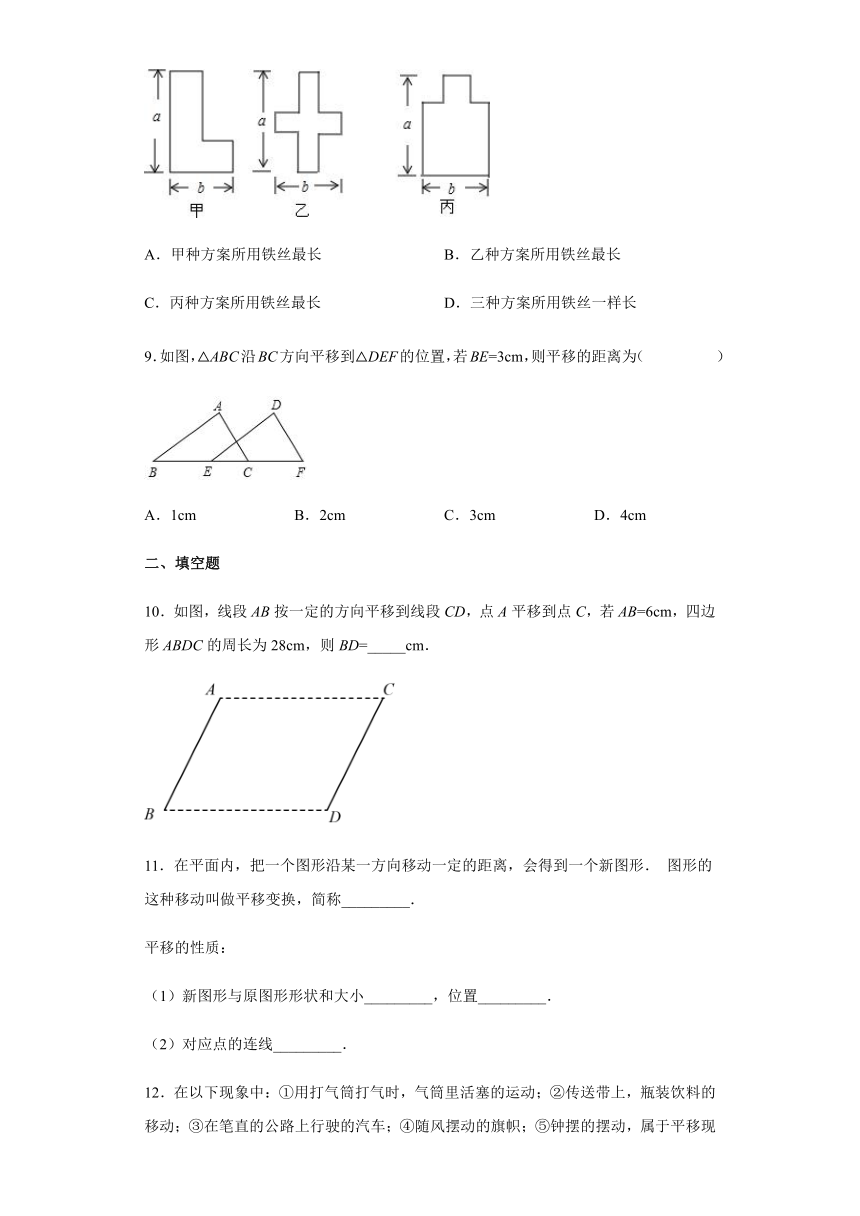
6.如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
7.下列现象中,属于平移的是( )
A.将一张纸沿它的中线折叠 B.飞碟的快速转动
C.翻开书中的每一页纸 D.电梯的上下移动
8.某数学兴趣小机开展动手操作活动,设计了如图所示的三种图形,现在计划用铁丝按照图制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
9.如图,△ABC沿BC方向平移到△DEF的位置,若BE=3cm,则平移的距离为( )
A.1cm B.2cm C.3cm D.4cm
二、填空题
10.如图,线段AB按一定的方向平移到线段CD,点A平移到点C,若AB=6cm,四边形ABDC的周长为28cm,则BD=_____cm.
11.在平面内,把一个图形沿某一方向移动一定的距离,会得到一个新图形. 图形的这种移动叫做平移变换,简称_________.
平移的性质:
(1)新图形与原图形形状和大小_________,位置_________.
(2)对应点的连线_________.
12.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有__(只填序号)
13.如图,一块长95m、宽55m的长方形土地,上面修了两条小路,宽都是5m,将阴影部分种上草坪,则草坪的面积是________m2.
三、解答题
14.如图,在三角形中,,,沿方向平移至,若,.
(1)求的长;
(2)求四边形的周长.
15.某宾馆重新装修后,准备在大厅的主楼梯上铺设某种红地毯,已知这种地毯售价为30元/m2,主楼梯宽2m,其侧面如图所示.
(1)求这个地毯的长是多少?
(2)求这个地毯的面积是多少平方米?
(3)求购买地毯至少需要多少元钱?
16.如图,将水平向右平移得到,,两点的距离为1,,.根据题意完成下列各题:
(1)和的数量关系为__________;和的位置关系为___________;
(2)求的度数;
(3)__________.
17.经过平移,△ABC的顶点A移到了点D,作出平移后的三角形.
试卷第1页,共3页
答案
1.A
2.C
3.C
4.C
5.C
6.C
7.D
8.D
9.C
10.8
11. 平移 完全相同 不同 平行且相等
12.①②③
13.4500
14.解:(1)∵ABC沿AB方向向右平移得到DEF,
∴AD=BE=CF,BC=EF=3cm,
∵AE=8cm,DB=2cm,
∴AD=BE=CF==3cm,
即;
(2)由平移的特征及(1)得
,.
∵,,
∴四边形的周长.
15.解:(1)地毯的长是:2.6+5.8=8.4(m);
(2)8.4×2=16.8(平方米);
(3)8.4×2×30=504(元).
16.解:(1)AC和DF的关系式为AC=DF,AC∥DF.
故答案为:AC=DF,AC∥DF;
(2)∵三角形ABC水平向右平移得到三角形DEF,
∴AB∥DE,
∵∠A=70°,
∴∠1=110°;
(3)BF=BE+CE+CF=1+2+1=4.
故答案为:4.
17.
答案第1页,共2页
一、单选题
1.下列图形中,把三角形ABC平移后能得到三角形DEF的是( )
2.如图,在7×7的方格纸中,每个小方格都是边长为1的小正方形,网格线的交点称格点,点A,点B是方格纸中的两个格点,找出格点C,使△ABC的面积为3,则满足条件的格点C的个数是( )
A.4个 B.5个 C.6个 D.8个
3.如图所示,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米40元,且知主楼梯道的宽为,其侧面如图所示,则买地毯至少需要( )元.
A.1881.6 B.768 C.1008 D.672
4.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=4,EF=8,CG=3,则图中阴影部分的面积为( )
A.16 B.20 C.26 D.12
5.下列命题是真命题的有( )
(1)过两点有且只有一条线段;(2)两点之间直线最短;(3)两条直线被第三条直线所截,同位角相等;(4)过一点有且只有一条直线与已知直线垂直;(5)平移前后连接各组对应点的线段平行(或共线)且相等.
A.0个 B.1个 C.2个 D.3个
6.如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
7.下列现象中,属于平移的是( )
A.将一张纸沿它的中线折叠 B.飞碟的快速转动
C.翻开书中的每一页纸 D.电梯的上下移动
8.某数学兴趣小机开展动手操作活动,设计了如图所示的三种图形,现在计划用铁丝按照图制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
9.如图,△ABC沿BC方向平移到△DEF的位置,若BE=3cm,则平移的距离为( )
A.1cm B.2cm C.3cm D.4cm
二、填空题
10.如图,线段AB按一定的方向平移到线段CD,点A平移到点C,若AB=6cm,四边形ABDC的周长为28cm,则BD=_____cm.
11.在平面内,把一个图形沿某一方向移动一定的距离,会得到一个新图形. 图形的这种移动叫做平移变换,简称_________.
平移的性质:
(1)新图形与原图形形状和大小_________,位置_________.
(2)对应点的连线_________.
12.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有__(只填序号)
13.如图,一块长95m、宽55m的长方形土地,上面修了两条小路,宽都是5m,将阴影部分种上草坪,则草坪的面积是________m2.
三、解答题
14.如图,在三角形中,,,沿方向平移至,若,.
(1)求的长;
(2)求四边形的周长.
15.某宾馆重新装修后,准备在大厅的主楼梯上铺设某种红地毯,已知这种地毯售价为30元/m2,主楼梯宽2m,其侧面如图所示.
(1)求这个地毯的长是多少?
(2)求这个地毯的面积是多少平方米?
(3)求购买地毯至少需要多少元钱?
16.如图,将水平向右平移得到,,两点的距离为1,,.根据题意完成下列各题:
(1)和的数量关系为__________;和的位置关系为___________;
(2)求的度数;
(3)__________.
17.经过平移,△ABC的顶点A移到了点D,作出平移后的三角形.
试卷第1页,共3页
答案
1.A
2.C
3.C
4.C
5.C
6.C
7.D
8.D
9.C
10.8
11. 平移 完全相同 不同 平行且相等
12.①②③
13.4500
14.解:(1)∵ABC沿AB方向向右平移得到DEF,
∴AD=BE=CF,BC=EF=3cm,
∵AE=8cm,DB=2cm,
∴AD=BE=CF==3cm,
即;
(2)由平移的特征及(1)得
,.
∵,,
∴四边形的周长.
15.解:(1)地毯的长是:2.6+5.8=8.4(m);
(2)8.4×2=16.8(平方米);
(3)8.4×2×30=504(元).
16.解:(1)AC和DF的关系式为AC=DF,AC∥DF.
故答案为:AC=DF,AC∥DF;
(2)∵三角形ABC水平向右平移得到三角形DEF,
∴AB∥DE,
∵∠A=70°,
∴∠1=110°;
(3)BF=BE+CE+CF=1+2+1=4.
故答案为:4.
17.
答案第1页,共2页
