2021-2022学年人教版数学九年级下册27.2.2相似三角形的性质提升练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册27.2.2相似三角形的性质提升练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 12:23:48 | ||
图片预览

文档简介
相似三角形的性质
一、单选题
1.如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B的度数为( )
A.45° B.50° C.55° D.60°
2.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )
A.2 B.3 C.6 D.54
3.如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,若S四边形BCFE=8,S△AEF=1,AF=3,则CF的长是( )
A.6 B.8 C.9 D.12
4.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,折痕为EF,点E、F分别在边BC、AB上,若△CDE与△ABC相似,则CE的长为( )
A. B. C.或 D.或
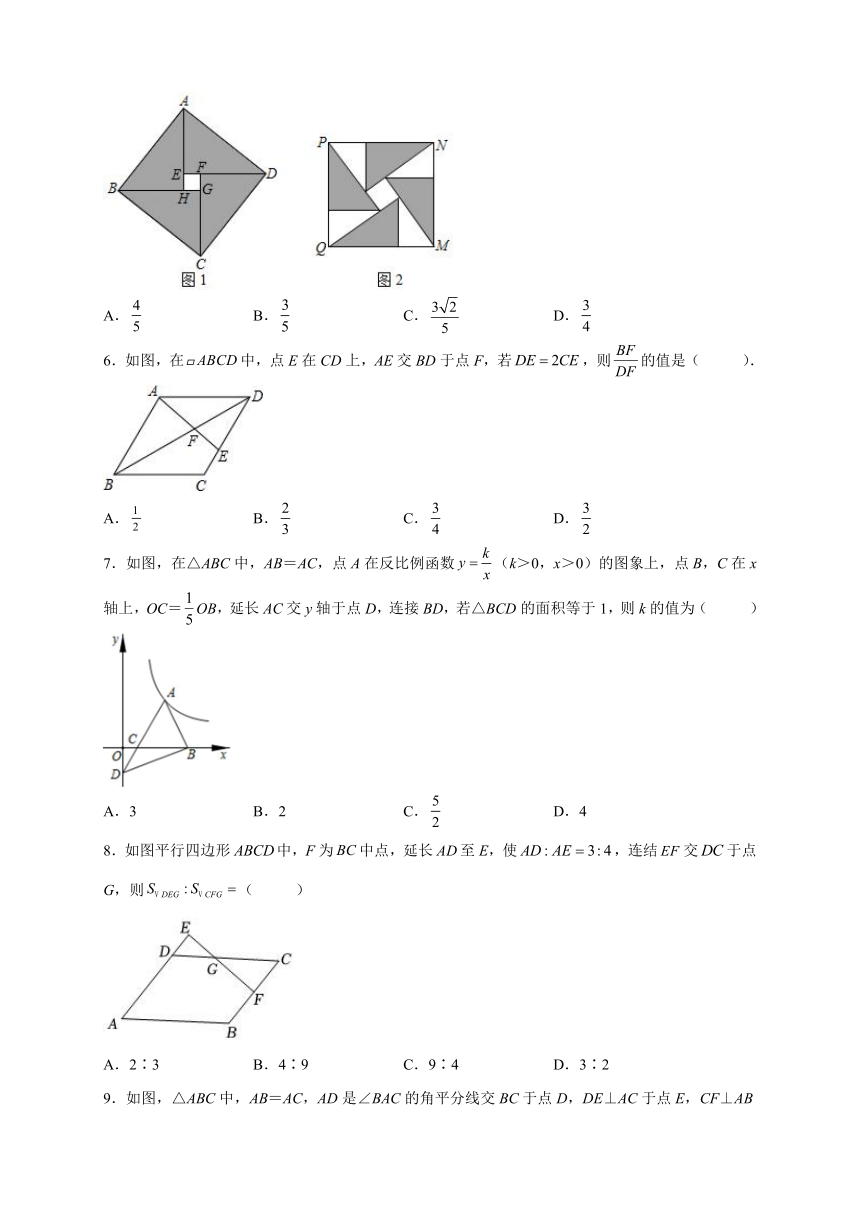
5.如图1是2002年北京国际数学家大会徽标图案,它是由4个全等的直角三角形和一个小正方形组成.把这4个全等直角三角形进行如图2的摆放,得到一个大正方形PQMN,若EF=,AD=,则为( )
A. B. C. D.
6.如图,在中,点E在CD上,AE交BD于点F,若,则的值是( ).
A. B. C. D.
7.如图,在△ABC中,AB=AC,点A在反比例函数(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为( )
A.3 B.2 C. D.4
8.如图平行四边形中,F为中点,延长至E,使,连结交于点G,则( )
A.2∶3 B.4∶9 C.9∶4 D.3∶2
9.如图,△ABC中,AB=AC,AD是∠BAC的角平分线交BC于点D,DE⊥AC于点E,CF⊥AB于点F,DE=3,则CF的长为( )
A.4 B.6 C.9 D.12
10.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则( )
A.1:4 B.1:5 C.1:6 D.1:7
11.如图所示,点D、E、F分别位于△ABC的三边上,且DE//BC,EF//AB.如果△ADE的面积为2,△CEF的面积为8,那么四边形BFED的面积是( )
A.4 B.6 C.8 D.10
12.如图,在矩形中,,,、为矩形外面的点,,,则EF=( )
A. B.15 C.20 D.
二、填空题
13.在△ABC中,∠ACD=∠B,作DE∥BC交AC于点E,若AD:DB=4:5,AC=9,AD的长为 ___.
14.如图,,点在上,与交于点,,,则的长为________.
15.如图,在矩形ABCD中,AB=8,AD=12,点E、F分别在边AB、CD上,点M为线段EF上一动点,过点M作EF的垂线分别交边AD、BC于点G、点H.若线段EF恰好平分矩形ABCD的面积,且DF=1,则GH的长为 _____.
16.如图,在Rt△ABC中,,,,点从点出发,沿方向以每秒个单位长度的速度向终点运动;同时,动点从点出发沿方向以每秒3个单位长度的速度向终点运动,设点运动的时间为秒,当是直角三角形时,的值为_______.
17.如图,正方形ABCD的边长为1,O为对角线BD的中点,点M在边AB上,且BM=2AM,点N在边BC上,且BN=AM,连接AN,MD交于点P,连接OP,则OP的长为___.
三、解答题
18.如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为4,求平行四边形ABCD的面积.
19.已知:如图,四边形ABCD是菱形,点M、N分别在边BC、CD上,连接AM、AN交对角线BD于E、F两点,且∠MAN=∠ABD.
(1)求证:AD2=BF DE.
(2)若=,求证EF∥MN.
20.如图所示,在三角形ABC中,D是AC上的一点.
(1)以AD为一边,在三角形ABC内求作∠ADE,使∠ADE=∠B,DE交AB于点E(要求用尺规作图,保留作图痕迹,不写作法)
(2)若AB=4,AD=1,BC=3,求DE的长.
21.如图,在△ABC中,AD是BC边上的中线,E,G分别是AC,DC的中点,F为DE延长线上的点,∠FCA=∠CEG.
(1)求证:AD=CF;
(2)连接AF,当AB=AC时,四边形ADCF是什么特殊四边形?请说明理由.
22.已知△ABC中,AC=BC,点D、E分别在AC、AB上,BD、CE交于点O.
(1)如图①,∠ACB =60°,AD=BE,求证:∠COD=60°;
(2)如图②,∠ACB=90°,AD=AC,AE=AB,求证:∠COD =90°;
(3)如图③,∠ACB=90°,AD=AC,BE=AB,猜想∠COD的大小并加以证明.
试卷第1页,共3页
参考答案:
1.A
解:解:∵△ABC∽△ACP,
∴∠ACB=∠APC=65°,
∵∠A=70°,
∴∠B=180°-∠A-∠ACB=180°-70°-65°=45°.
故选:A.
2.C
解:解:∵△ABC∽△DEF,相似比为3:1
∴△ABC的周长:△DEF的周长=3:1
∵△ABC的周长为18
∴△DEF的周长为6
故选C.
3.A
解:解:∵S四边形BCFE=8,S△AEF=1,
,
∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴,
∵AF=3,
∴AC=9,
∴CF=AC﹣AF=9﹣3=6,
故选:A.
4.D
解:解:∵∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,
∴AB=5,BE=DE,BE=4﹣CE,
当△CDE∽△CBA时,
则 ,
∴ ,
解得CE= ;
当△CDE∽△CAB时,
则 ,
∴ ,
解得CE=
由上可得,CE的长为或.
故选:D.
5.A
解:解:如图1中,设AE=DF=x,
在Rt△ADE中,AD2=AE2+DE2,
∴ ,
∴x=4或,
∴AE=4,,
如图2中,
,
,,
,
,
∴,
∴NQ=3,
∴,
∴,
故选:A.
6.D
解:解:∵DE=2CE,
∴DE=CD,
∴,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴,
∵AB∥DE,
∴△DFE∽△BFA,
∴,
∴,
故选:D.
7.A
解:解:作AE⊥BC于E,连接OA,
∵AB=AC,
∴CE=BE,
∵OC=OB,
∴OC= BC=×2CE= CE,
∵AE∥OD,
∴△COD∽△CEA,
∴ ,
∵△BCD的面积等于1,OC=OB,
∴S△COD=S△BCD=,
∴S△CEA=4×=1,
∵OC=CE,
∴S△AOC=S△CEA=,
∴S△AOE=+1= ,
∵S△AOE=k(k>0),
∴k=3,
故选A.
8.B
解:解:∵,
∴设,
∴,
∵四边形ABCD是平行四边形,
∴,,
∵点F是BC的中点,
∴,
∵,
∴,
∴,
故选B.
9.B
解:解:,
,
由题意可知:,
,
,
设,
,
,
.
故选:B.
10.C
解:解:∵O为平行四边形ABCD对角线的交点,
∴DO=BO,,
又∵E为OD的中点,
∴,
∴DE:EB=1:3,
又∵,
∴,
∴,
∴,
∵,
∴,
∴
故选:C.
11.C
解:解:∵DE//BC,EF//AB,
∴∠AED=∠C,∠ADE=∠B,∠EFC=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC.
∴,
而S△ADE=2,S△CEF=8,
∴AE:EC=1:2,
设AE=k,则EC=2k,AC=3k.
则AE:AC=k:3k=1:3,
设S四边形BFED=S;
∵DE//BC,
∴△ADE∽△ABC,
∴,
即,
解得:S=8,
即四边形BFED的面积为8.
故选:C.
12.A
解:解:延长FA交EB的延长线于点M,如图所示:
四边形ABCD是矩形,
,,,
,,
,
是直角三角形,,
同理:是直角三角形,
,
,
,
同理:,
在和中,
,
,
,,
,
,
,
,
,即,
解得:,,
,,
.
故选:A.
13.6
解:解:∵AD:DB=4:5,
∴AD:AB=4:9,
∵DE//BC,
∴AD:AB=AE:AC=4:9,
∵AC=9,
∴AE=4,
∵DE//BC,
∴∠ADE=∠B,
∵∠ACD=∠B,
∴∠ACD=∠ADE,
又∵∠A=∠A,
∴△ADE∽△ACD,
∴AD:AC=AE:AD,
∴AD2=AC×AE=9×4=36,
∵AD>0,
∴AD=6,
故答案为:6.
14.##
解:解:∵,,,
∴,
∴,
∴,
∵,
∴,
∴,
即,
∴,
故答案为:.
15.
解:解:过点G作于点K,过点F作于点N,交GH于点O,交GK于点P,如下图,
平分矩形ABCD的面积,
,
,,
四边形ADFN是矩形,
,,
.
,,
,
,
.
又,
,
,
.
在中,.
16.或
解:解:由题意得:
,
,,
.
当时,
,
.
,
.
.
.
解得:.
当时,
,
.
,
.
.
.
解得:.
综上所述,当是直角三角形时,的值为或.
故答案为:或.
17.
解:解:设AN和BD交于点Q,
∵正方形ABCD的边长为1,
∴,
∵BM=2AM,
∴BM+AM=AB=1,
∴AM=BN=,BM=,
∵AD∥BN,
∴△NQB∽△AQD,
∴,
∴DQ=3BQ,
∴,BQ=,
∵O是BD的中点,
∴OD=,
∴OQ=DQ-OD=,
在△ADM和△BAN中,
,
∴△ADM≌△BAN(SAS),
∴∠ADM=∠BAN,
∵∠PAD+∠BAN=90°,
∴∠PAD+∠ADM=90°,
∴∠APD=90°,
∵∠DAM=90°,AM=,AD=1,
∴DM= ,
∵S△ADM=×AD AM=×DM AP,
∴,
∴,
∴PD=DM-PM=,
∵△ADM≌△BAN,
∴AN=DM= ,
∵,
∴,,
∴,
如图,过点O作OG⊥DM于点G,
∵OG∥PQ,
∴△OGD∽△QPD,
∴,
∴,,
∴,
∴.
故答案为:.
18.(1)见解析
(2)48
(1)
解:四边形是平行四边形,
,.
,
.
(2)
解:四边形是平行四边形,
,.
,
.
解:由(1)得:.
,
.
.
.
.
四边形是平行四边形,
,即,.
,.
.
又,
.
.
.
19.(1)见解析
(2)见解析
(1)
证明:∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠AED=∠ABD+∠BAE,∠BAF=∠MAN+∠BAE,∠MAN=∠ABD,
∴∠AED=∠BAF,
∴△AED∽△FAB,
∴,即AD AB=BF DE,
∴AB2=BF DE,
∵AB=AD,
∴AD2=BF DE;
(2)
∵四边形ABCD是菱形,
∴AD=BC,ADBC,
∴△BME∽△DAE,
∴,
∵,
∴,
∴,
∴,
∵∠C=∠C,
∴△CMN∽△CBD,
∴∠CMN=∠CBD,
∴MNBD,
即EFMN.
20.(1)见解析
(2)
(1)
如图,∠ADE为所作;
(2)
∵∠DAE=∠BAC,∠ADE=∠B,
∴△ADE∽△ABC,
∴,即=,
∴DE=.
21.(1)证明见解析
(2)四边形ADCF是矩形,理由见解析
(1)
证明:∵E,G分别是AC,DC的中点,
∴EG是△CAD的中位线,
∴EG=AD,,
∵∠FCA=∠CEG,
∴,
∴△DEG∽△DFC,
∴==,
∴EG=CF,
∴AD=CF;
(2)
解:当AB=AC时,四边形ADCF是矩形,
理由如下:
∵,,AD=CF,
∴,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,
∴平行四边形ADCF是矩形.
22.(1)见解析
(2)见解析
(3)∠COD=45°,证明见解析
(1)
证明:∵AC=BC,∠ACB =60°,
∴△ABC为等边三角形,
∴∠A=∠ABC=60°,
∵AD=BE,
∴△ABD≌△BCE,
∴∠ABD=∠BCE,
∴∠COD=∠CBD+∠BCE=∠CBD+∠ABD=60°;
(2)
证明:如图,过A作AF//BC交CE的延长线于F,
∴△AEF∽△BEC,
∴,
∵AE=AB,
∴ ,
∴,
∵AC=BC,AD=AC,
∴ ,
∵∠ACB=90°,AF//BC,
∴∠CAF+∠ACB=90°,
∴∠CAF=∠ACB=90°,
∴△AFC≌△CDB,
∴∠ACE=∠CBD,
∴∠COD=∠CBD+∠BCE=∠ACE+∠BCE=90°;
(3)
解:∠COD=45° ,理由如下:
设BE =a,则AB=4a,
∵AC=BC,∠ACB=90°,
∴ ,∠ABC=∠A=45°,
∴AC=BC=,
∵AD=AC,
∴ ,
∴ , ,
∴,
∵∠ABC=∠A=45°,
∴△ABD∽△BCE,
∴∠ABD=∠BCE,
∴∠COD=∠CBD+∠BCE=∠CBD+∠ABD=45°.
答案第1页,共2页
一、单选题
1.如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B的度数为( )
A.45° B.50° C.55° D.60°
2.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )
A.2 B.3 C.6 D.54
3.如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,若S四边形BCFE=8,S△AEF=1,AF=3,则CF的长是( )
A.6 B.8 C.9 D.12
4.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,折痕为EF,点E、F分别在边BC、AB上,若△CDE与△ABC相似,则CE的长为( )
A. B. C.或 D.或
5.如图1是2002年北京国际数学家大会徽标图案,它是由4个全等的直角三角形和一个小正方形组成.把这4个全等直角三角形进行如图2的摆放,得到一个大正方形PQMN,若EF=,AD=,则为( )
A. B. C. D.
6.如图,在中,点E在CD上,AE交BD于点F,若,则的值是( ).
A. B. C. D.
7.如图,在△ABC中,AB=AC,点A在反比例函数(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为( )
A.3 B.2 C. D.4
8.如图平行四边形中,F为中点,延长至E,使,连结交于点G,则( )
A.2∶3 B.4∶9 C.9∶4 D.3∶2
9.如图,△ABC中,AB=AC,AD是∠BAC的角平分线交BC于点D,DE⊥AC于点E,CF⊥AB于点F,DE=3,则CF的长为( )
A.4 B.6 C.9 D.12
10.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则( )
A.1:4 B.1:5 C.1:6 D.1:7
11.如图所示,点D、E、F分别位于△ABC的三边上,且DE//BC,EF//AB.如果△ADE的面积为2,△CEF的面积为8,那么四边形BFED的面积是( )
A.4 B.6 C.8 D.10
12.如图,在矩形中,,,、为矩形外面的点,,,则EF=( )
A. B.15 C.20 D.
二、填空题
13.在△ABC中,∠ACD=∠B,作DE∥BC交AC于点E,若AD:DB=4:5,AC=9,AD的长为 ___.
14.如图,,点在上,与交于点,,,则的长为________.
15.如图,在矩形ABCD中,AB=8,AD=12,点E、F分别在边AB、CD上,点M为线段EF上一动点,过点M作EF的垂线分别交边AD、BC于点G、点H.若线段EF恰好平分矩形ABCD的面积,且DF=1,则GH的长为 _____.
16.如图,在Rt△ABC中,,,,点从点出发,沿方向以每秒个单位长度的速度向终点运动;同时,动点从点出发沿方向以每秒3个单位长度的速度向终点运动,设点运动的时间为秒,当是直角三角形时,的值为_______.
17.如图,正方形ABCD的边长为1,O为对角线BD的中点,点M在边AB上,且BM=2AM,点N在边BC上,且BN=AM,连接AN,MD交于点P,连接OP,则OP的长为___.
三、解答题
18.如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为4,求平行四边形ABCD的面积.
19.已知:如图,四边形ABCD是菱形,点M、N分别在边BC、CD上,连接AM、AN交对角线BD于E、F两点,且∠MAN=∠ABD.
(1)求证:AD2=BF DE.
(2)若=,求证EF∥MN.
20.如图所示,在三角形ABC中,D是AC上的一点.
(1)以AD为一边,在三角形ABC内求作∠ADE,使∠ADE=∠B,DE交AB于点E(要求用尺规作图,保留作图痕迹,不写作法)
(2)若AB=4,AD=1,BC=3,求DE的长.
21.如图,在△ABC中,AD是BC边上的中线,E,G分别是AC,DC的中点,F为DE延长线上的点,∠FCA=∠CEG.
(1)求证:AD=CF;
(2)连接AF,当AB=AC时,四边形ADCF是什么特殊四边形?请说明理由.
22.已知△ABC中,AC=BC,点D、E分别在AC、AB上,BD、CE交于点O.
(1)如图①,∠ACB =60°,AD=BE,求证:∠COD=60°;
(2)如图②,∠ACB=90°,AD=AC,AE=AB,求证:∠COD =90°;
(3)如图③,∠ACB=90°,AD=AC,BE=AB,猜想∠COD的大小并加以证明.
试卷第1页,共3页
参考答案:
1.A
解:解:∵△ABC∽△ACP,
∴∠ACB=∠APC=65°,
∵∠A=70°,
∴∠B=180°-∠A-∠ACB=180°-70°-65°=45°.
故选:A.
2.C
解:解:∵△ABC∽△DEF,相似比为3:1
∴△ABC的周长:△DEF的周长=3:1
∵△ABC的周长为18
∴△DEF的周长为6
故选C.
3.A
解:解:∵S四边形BCFE=8,S△AEF=1,
,
∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴,
∵AF=3,
∴AC=9,
∴CF=AC﹣AF=9﹣3=6,
故选:A.
4.D
解:解:∵∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,
∴AB=5,BE=DE,BE=4﹣CE,
当△CDE∽△CBA时,
则 ,
∴ ,
解得CE= ;
当△CDE∽△CAB时,
则 ,
∴ ,
解得CE=
由上可得,CE的长为或.
故选:D.
5.A
解:解:如图1中,设AE=DF=x,
在Rt△ADE中,AD2=AE2+DE2,
∴ ,
∴x=4或,
∴AE=4,,
如图2中,
,
,,
,
,
∴,
∴NQ=3,
∴,
∴,
故选:A.
6.D
解:解:∵DE=2CE,
∴DE=CD,
∴,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴,
∵AB∥DE,
∴△DFE∽△BFA,
∴,
∴,
故选:D.
7.A
解:解:作AE⊥BC于E,连接OA,
∵AB=AC,
∴CE=BE,
∵OC=OB,
∴OC= BC=×2CE= CE,
∵AE∥OD,
∴△COD∽△CEA,
∴ ,
∵△BCD的面积等于1,OC=OB,
∴S△COD=S△BCD=,
∴S△CEA=4×=1,
∵OC=CE,
∴S△AOC=S△CEA=,
∴S△AOE=+1= ,
∵S△AOE=k(k>0),
∴k=3,
故选A.
8.B
解:解:∵,
∴设,
∴,
∵四边形ABCD是平行四边形,
∴,,
∵点F是BC的中点,
∴,
∵,
∴,
∴,
故选B.
9.B
解:解:,
,
由题意可知:,
,
,
设,
,
,
.
故选:B.
10.C
解:解:∵O为平行四边形ABCD对角线的交点,
∴DO=BO,,
又∵E为OD的中点,
∴,
∴DE:EB=1:3,
又∵,
∴,
∴,
∴,
∵,
∴,
∴
故选:C.
11.C
解:解:∵DE//BC,EF//AB,
∴∠AED=∠C,∠ADE=∠B,∠EFC=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC.
∴,
而S△ADE=2,S△CEF=8,
∴AE:EC=1:2,
设AE=k,则EC=2k,AC=3k.
则AE:AC=k:3k=1:3,
设S四边形BFED=S;
∵DE//BC,
∴△ADE∽△ABC,
∴,
即,
解得:S=8,
即四边形BFED的面积为8.
故选:C.
12.A
解:解:延长FA交EB的延长线于点M,如图所示:
四边形ABCD是矩形,
,,,
,,
,
是直角三角形,,
同理:是直角三角形,
,
,
,
同理:,
在和中,
,
,
,,
,
,
,
,
,即,
解得:,,
,,
.
故选:A.
13.6
解:解:∵AD:DB=4:5,
∴AD:AB=4:9,
∵DE//BC,
∴AD:AB=AE:AC=4:9,
∵AC=9,
∴AE=4,
∵DE//BC,
∴∠ADE=∠B,
∵∠ACD=∠B,
∴∠ACD=∠ADE,
又∵∠A=∠A,
∴△ADE∽△ACD,
∴AD:AC=AE:AD,
∴AD2=AC×AE=9×4=36,
∵AD>0,
∴AD=6,
故答案为:6.
14.##
解:解:∵,,,
∴,
∴,
∴,
∵,
∴,
∴,
即,
∴,
故答案为:.
15.
解:解:过点G作于点K,过点F作于点N,交GH于点O,交GK于点P,如下图,
平分矩形ABCD的面积,
,
,,
四边形ADFN是矩形,
,,
.
,,
,
,
.
又,
,
,
.
在中,.
16.或
解:解:由题意得:
,
,,
.
当时,
,
.
,
.
.
.
解得:.
当时,
,
.
,
.
.
.
解得:.
综上所述,当是直角三角形时,的值为或.
故答案为:或.
17.
解:解:设AN和BD交于点Q,
∵正方形ABCD的边长为1,
∴,
∵BM=2AM,
∴BM+AM=AB=1,
∴AM=BN=,BM=,
∵AD∥BN,
∴△NQB∽△AQD,
∴,
∴DQ=3BQ,
∴,BQ=,
∵O是BD的中点,
∴OD=,
∴OQ=DQ-OD=,
在△ADM和△BAN中,
,
∴△ADM≌△BAN(SAS),
∴∠ADM=∠BAN,
∵∠PAD+∠BAN=90°,
∴∠PAD+∠ADM=90°,
∴∠APD=90°,
∵∠DAM=90°,AM=,AD=1,
∴DM= ,
∵S△ADM=×AD AM=×DM AP,
∴,
∴,
∴PD=DM-PM=,
∵△ADM≌△BAN,
∴AN=DM= ,
∵,
∴,,
∴,
如图,过点O作OG⊥DM于点G,
∵OG∥PQ,
∴△OGD∽△QPD,
∴,
∴,,
∴,
∴.
故答案为:.
18.(1)见解析
(2)48
(1)
解:四边形是平行四边形,
,.
,
.
(2)
解:四边形是平行四边形,
,.
,
.
解:由(1)得:.
,
.
.
.
.
四边形是平行四边形,
,即,.
,.
.
又,
.
.
.
19.(1)见解析
(2)见解析
(1)
证明:∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠AED=∠ABD+∠BAE,∠BAF=∠MAN+∠BAE,∠MAN=∠ABD,
∴∠AED=∠BAF,
∴△AED∽△FAB,
∴,即AD AB=BF DE,
∴AB2=BF DE,
∵AB=AD,
∴AD2=BF DE;
(2)
∵四边形ABCD是菱形,
∴AD=BC,ADBC,
∴△BME∽△DAE,
∴,
∵,
∴,
∴,
∴,
∵∠C=∠C,
∴△CMN∽△CBD,
∴∠CMN=∠CBD,
∴MNBD,
即EFMN.
20.(1)见解析
(2)
(1)
如图,∠ADE为所作;
(2)
∵∠DAE=∠BAC,∠ADE=∠B,
∴△ADE∽△ABC,
∴,即=,
∴DE=.
21.(1)证明见解析
(2)四边形ADCF是矩形,理由见解析
(1)
证明:∵E,G分别是AC,DC的中点,
∴EG是△CAD的中位线,
∴EG=AD,,
∵∠FCA=∠CEG,
∴,
∴△DEG∽△DFC,
∴==,
∴EG=CF,
∴AD=CF;
(2)
解:当AB=AC时,四边形ADCF是矩形,
理由如下:
∵,,AD=CF,
∴,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,
∴平行四边形ADCF是矩形.
22.(1)见解析
(2)见解析
(3)∠COD=45°,证明见解析
(1)
证明:∵AC=BC,∠ACB =60°,
∴△ABC为等边三角形,
∴∠A=∠ABC=60°,
∵AD=BE,
∴△ABD≌△BCE,
∴∠ABD=∠BCE,
∴∠COD=∠CBD+∠BCE=∠CBD+∠ABD=60°;
(2)
证明:如图,过A作AF//BC交CE的延长线于F,
∴△AEF∽△BEC,
∴,
∵AE=AB,
∴ ,
∴,
∵AC=BC,AD=AC,
∴ ,
∵∠ACB=90°,AF//BC,
∴∠CAF+∠ACB=90°,
∴∠CAF=∠ACB=90°,
∴△AFC≌△CDB,
∴∠ACE=∠CBD,
∴∠COD=∠CBD+∠BCE=∠ACE+∠BCE=90°;
(3)
解:∠COD=45° ,理由如下:
设BE =a,则AB=4a,
∵AC=BC,∠ACB=90°,
∴ ,∠ABC=∠A=45°,
∴AC=BC=,
∵AD=AC,
∴ ,
∴ , ,
∴,
∵∠ABC=∠A=45°,
∴△ABD∽△BCE,
∴∠ABD=∠BCE,
∴∠COD=∠CBD+∠BCE=∠CBD+∠ABD=45°.
答案第1页,共2页
