2021-2022学年人教版数学九年级下册27.2.3相似三角形应用举例课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册27.2.3相似三角形应用举例课后提升(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 00:00:00 | ||
图片预览




文档简介
相似三角形应用举例
一、单选题
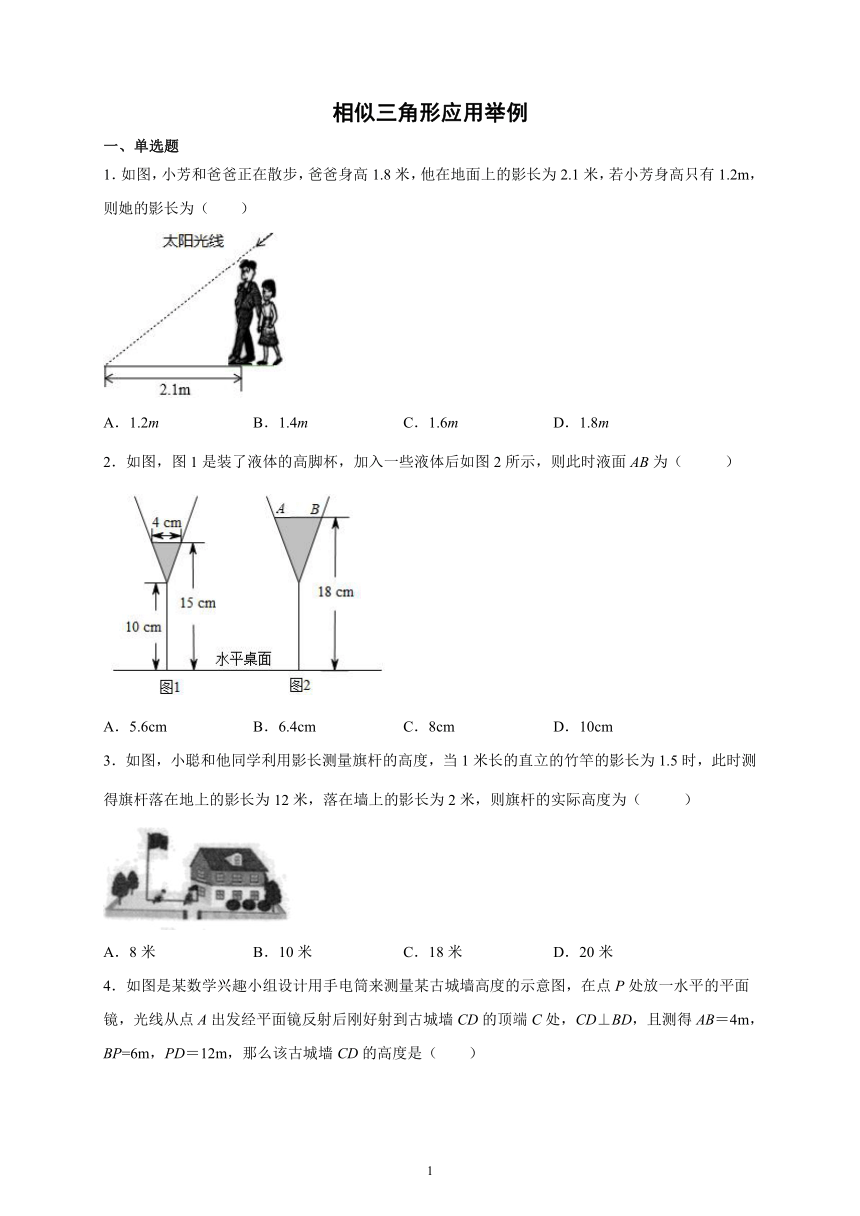
1.如图,小芳和爸爸正在散步,爸爸身高1.8米,他在地面上的影长为2.1米,若小芳身高只有1.2m,则她的影长为( )
A.1.2m B.1.4m C.1.6m D.1.8m
2.如图,图1是装了液体的高脚杯,加入一些液体后如图2所示,则此时液面AB为( )
A.5.6cm B.6.4cm C.8cm D.10cm
3.如图,小聪和他同学利用影长测量旗杆的高度,当1米长的直立的竹竿的影长为1.5时,此时测得旗杆落在地上的影长为12米,落在墙上的影长为2米,则旗杆的实际高度为( )
A.8米 B.10米 C.18米 D.20米
4.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
5.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为( )
A.14cm B.16cm C.25cm D.32cm
6.如图,广场上有一盏路灯挂在高的电线杆顶上,记电线杆的底部为.把路灯看成一个点光源,一名身高的女孩站在点处,,若女孩以为半径绕着电线杆走一个圆圈,则女孩的影子扫过的图形的面积为( )
A. B. C. D.
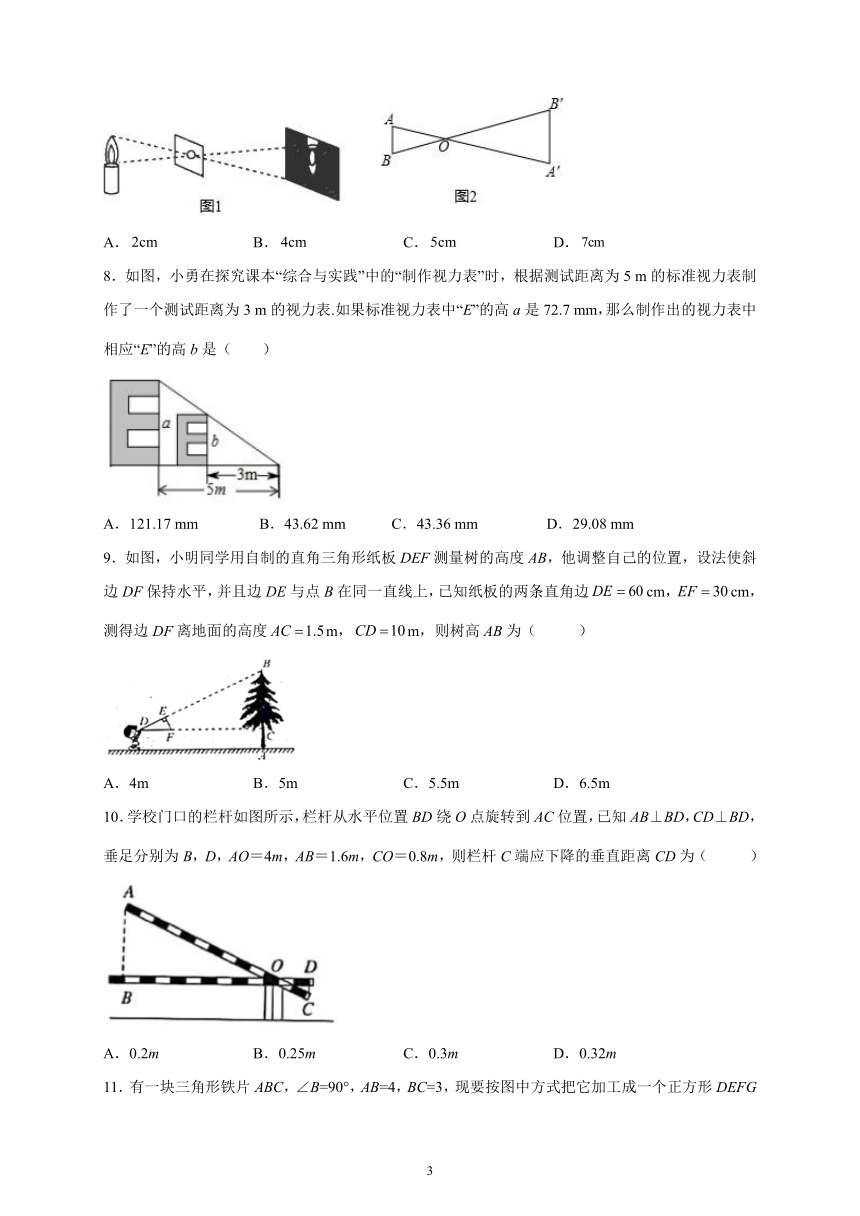
7.在物理课中同学们曾学过小孔成像:在较暗的屋子里,把一支点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间数一块钻有小孔章的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像(如图1),这种现象就是小孔成像,在图2中,如果蜡烛火焰图1根B到孔О的距离为,火焰根的像到孔O的距离为10cm,蜡烛火焰的高度为,那么倒立的像的高度为( )
A. B. C. D.
8.如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
A.121.17 mm B.43.62 mm C.43.36 mm D.29.08 mm
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边cm,cm,测得边DF离地面的高度m,m,则树高AB为( )
A.4m B.5m C.5.5m D.6.5m
10.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=0.8m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.25m C.0.3m D.0.32m
11.有一块三角形铁片ABC,∠B=90°,AB=4,BC=3,现要按图中方式把它加工成一个正方形DEFG(加工中的损耗忽略不计),则正方形DEFG的边长为( )
A. B. C. D.
12.如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚AD和BC交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=4cm,则AB的长是( )
A.16cm B.12cm C.8cm D.6cm
13.如图,小明在A时测得某树的影长为4米,B时又测得该树的影长为1米,若两次日照的光线互相垂直,则树的高度为( )米.
A.2 B.4 C.6 D.8
14.如图是测量河宽的示意图,测得,,,则河宽的长为( )
A. B. C. D.
二、填空题
15.(1)相似三角形的对应角_______,对应边_______.
(2)相似三角形对应线段的比等于_______.
(3)相似三角形周长的比等于_______.
(4)相似三角形面积的比等于_______.
16.如图,小红把梯子AB斜靠在墙壁上,梯脚B距墙2米,此时D点距墙1.8米,BD长0.6米,则梯子AB的长为_____米.
17.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 _____米.
18.《九章算术》是我国古代数学名著,书中有如下问题:“今有井径五尺,不知其深,立三尺木于井上,从木末望水岸,入径五寸.问井深几何?”意思是:如图,井径尺,立木高尺,寸尺,则井深为______尺.
三、解答题
19.如图两栋高楼东西方向并排,它们的高米,米,且米.
(1)如果你在P点的位置,你能看到高楼BD吗?(人的高度不计)
(2)如果在高楼AC的西边要想看到高楼BD,至少离高楼AC多少米?
20.王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
21.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上).
22.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
23.如图1是某物体的支架实物图,图2是其右侧部分抽象后的几何图形,其中是支杆上一可转动点,,是中间竖杆上的一动点,当点沿滑动时,点随之在地面上滑动,点是动点能到达的最顶端位置,当运动到点时,与重合于竖杆,经测量,设,竖杆的最下端到地面的距离.
(1)求的长.
(2)当点运动时,试求出与的函数关系式.
试卷第1页,共3页
参考答案:
1.B
解:设小芳的影长为h米
∵同一时刻物高与影长成正比
∴
解得h=1.4
故选B.
2.B
解:依题意,两高脚杯中的液体部分两三角形相似,则
解得.
故选B
3.B
解:如图,AB为旗杆,AC为旗杆在地上的影长12米,CD为旗杆落在墙上的影长2米,延长AC,BD交于点E
由题意知,AE是旗杆在地上的影长
∴
∵1米长的直立的竹竿的影长为1.5米
∴
∴
解得:
∴
∴
故选B.
4.A
解:如图,根据反射的性质可得∠APE=∠CPE
∵EP⊥BD
∴∠APB=∠CPD
∵AB⊥BD,CD⊥BD
∴∠ABP=∠CDP=90°
∴△ABP∽△CDP
∴
∴
故选:A
5.B
解:如图,过作于 过作于
由小孔成像原理可得:
而
所以(cm),经检验符合题意.
故选B
6.C
解:如下图所示:
设AP=x,由题意可知:△COA∽△BPA,
∴,代入数据,,,
∴,解得,
∴所以人影扫过的面积是,
故选:C.
7.C
解:如下图所示:
∵AB∥A’B’,
∴△ABO∽△A’B’O,
∴,
由题意知:,代入上式中,
解得:.
故选:C.
8.B
解:如下图所示:
由题意可知:,
故有:,即,解得,
故选:B.
9.D
解:依题意,
cm,cm,m,m,
m
m
故选D
10.D
解:∵AB⊥BD,CD⊥BD,
∴∠ABO=∠CDO=90°,
又∵∠AOB=∠COD,
∴△ABO∽△CDO,
则,
∵AO=4m,AB=1.6m,CO=0.8m,
∴,
解得:CD=0.32m,
故选:D.
11.D
解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵∠B=90°,AB=4,BC=3,
∴AC=,
∵S△ABC=AB BC=AC BP,
∴BP=.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴.
设DE=x,则有:,
解得x=,
故选:D.
12.B
解:∵OA=3OD,OB=3CO,
∴OA:OD=BO:CO=3:1,∠AOB=∠DOC,
∴△AOB∽△DOC,
∴,
∴AB=3CD,
∵CD=4cm,
∴AB=12cm,
故选:B
13.A
解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=1m,FD=4m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴△EDC∽△FDC,
∴,即DC2=ED FD=1×4=4,
解得CD=2m.
故选A.
14.D
解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故选:D.
15. 相等 成比例 相似比 相似比 相似比的平方
解:略
16.6
解:,
;
,
,
;
设梯子AB的长为x米,
,
,即梯子的长度为6米.
故答案为:6
17.
解:如图,
∵北岸相邻的两根电线杆被南岸的5棵树遮挡住,
∴,,
∵,
∴,
,
∵,P到AB的距离即,
∴,
解得:,
∴河宽为36米,
故答案为:36.
18.27
解:∵,
∴,
∴,
即,
解得,
故井深为27尺.
故答案为:27
19.(1)不能看到高楼BD
(2)至少离高楼20米
(1)
解:不能看到高楼BD.
如图,连接PA并延长,交DB的延长线于点F
∵
∴在P点不能看到高楼BD.
(2)
解:至少离高楼为20米
设米
∵
∴
∴
∴
解得,经检验是分式方程的解
∴至少离高楼为20米.
20.(1)18m
(2)3.6m
解:(1)
如图1,
∵PMBD,
∴△APM∽△ABD,
,即,
∴AP=AB,
∵QB=AP,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)
如图2,他在路灯AC下的影子为BN,
∵BMAC,
∴△NBM∽△NAC,
∴,即,解得BN=3.6.
答:当他走到路灯BD时,他在路灯AC下的影长是3.6m.
21.步
解:由题意可知:,AH=15
∵H为GD的中点,K为DE的中点
DH=100,DK=100
∵AH∥DK
∴∠CDK=∠A
而∠CKD=∠AHD
∴
∴
即,
∴
答:出南门步恰好看到位于A处的树木.
22.(1)米
(2)设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即
(1)
解:标注点如下图:
根据题意在和,
,
,
,
分别为的中点,
,
,
(米);
(2)
解:设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即,过程如下:
根据题意作如下图形,
根据题意在和,
,
,
,
,
,
(米);
小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即即可.
23.(1)80cm;(2)
解:(1)∵当运动到点时,与重合于竖杆,
∴由题意可得;
(2)
如图,过点作于点,
,,
,
,
,
,
整理可得:.
答案第1页,共2页
一、单选题
1.如图,小芳和爸爸正在散步,爸爸身高1.8米,他在地面上的影长为2.1米,若小芳身高只有1.2m,则她的影长为( )
A.1.2m B.1.4m C.1.6m D.1.8m
2.如图,图1是装了液体的高脚杯,加入一些液体后如图2所示,则此时液面AB为( )
A.5.6cm B.6.4cm C.8cm D.10cm
3.如图,小聪和他同学利用影长测量旗杆的高度,当1米长的直立的竹竿的影长为1.5时,此时测得旗杆落在地上的影长为12米,落在墙上的影长为2米,则旗杆的实际高度为( )
A.8米 B.10米 C.18米 D.20米
4.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
5.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为( )
A.14cm B.16cm C.25cm D.32cm
6.如图,广场上有一盏路灯挂在高的电线杆顶上,记电线杆的底部为.把路灯看成一个点光源,一名身高的女孩站在点处,,若女孩以为半径绕着电线杆走一个圆圈,则女孩的影子扫过的图形的面积为( )
A. B. C. D.
7.在物理课中同学们曾学过小孔成像:在较暗的屋子里,把一支点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间数一块钻有小孔章的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像(如图1),这种现象就是小孔成像,在图2中,如果蜡烛火焰图1根B到孔О的距离为,火焰根的像到孔O的距离为10cm,蜡烛火焰的高度为,那么倒立的像的高度为( )
A. B. C. D.
8.如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
A.121.17 mm B.43.62 mm C.43.36 mm D.29.08 mm
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边cm,cm,测得边DF离地面的高度m,m,则树高AB为( )
A.4m B.5m C.5.5m D.6.5m
10.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=0.8m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.25m C.0.3m D.0.32m
11.有一块三角形铁片ABC,∠B=90°,AB=4,BC=3,现要按图中方式把它加工成一个正方形DEFG(加工中的损耗忽略不计),则正方形DEFG的边长为( )
A. B. C. D.
12.如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚AD和BC交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=4cm,则AB的长是( )
A.16cm B.12cm C.8cm D.6cm
13.如图,小明在A时测得某树的影长为4米,B时又测得该树的影长为1米,若两次日照的光线互相垂直,则树的高度为( )米.
A.2 B.4 C.6 D.8
14.如图是测量河宽的示意图,测得,,,则河宽的长为( )
A. B. C. D.
二、填空题
15.(1)相似三角形的对应角_______,对应边_______.
(2)相似三角形对应线段的比等于_______.
(3)相似三角形周长的比等于_______.
(4)相似三角形面积的比等于_______.
16.如图,小红把梯子AB斜靠在墙壁上,梯脚B距墙2米,此时D点距墙1.8米,BD长0.6米,则梯子AB的长为_____米.
17.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 _____米.
18.《九章算术》是我国古代数学名著,书中有如下问题:“今有井径五尺,不知其深,立三尺木于井上,从木末望水岸,入径五寸.问井深几何?”意思是:如图,井径尺,立木高尺,寸尺,则井深为______尺.
三、解答题
19.如图两栋高楼东西方向并排,它们的高米,米,且米.
(1)如果你在P点的位置,你能看到高楼BD吗?(人的高度不计)
(2)如果在高楼AC的西边要想看到高楼BD,至少离高楼AC多少米?
20.王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
21.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上).
22.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
23.如图1是某物体的支架实物图,图2是其右侧部分抽象后的几何图形,其中是支杆上一可转动点,,是中间竖杆上的一动点,当点沿滑动时,点随之在地面上滑动,点是动点能到达的最顶端位置,当运动到点时,与重合于竖杆,经测量,设,竖杆的最下端到地面的距离.
(1)求的长.
(2)当点运动时,试求出与的函数关系式.
试卷第1页,共3页
参考答案:
1.B
解:设小芳的影长为h米
∵同一时刻物高与影长成正比
∴
解得h=1.4
故选B.
2.B
解:依题意,两高脚杯中的液体部分两三角形相似,则
解得.
故选B
3.B
解:如图,AB为旗杆,AC为旗杆在地上的影长12米,CD为旗杆落在墙上的影长2米,延长AC,BD交于点E
由题意知,AE是旗杆在地上的影长
∴
∵1米长的直立的竹竿的影长为1.5米
∴
∴
解得:
∴
∴
故选B.
4.A
解:如图,根据反射的性质可得∠APE=∠CPE
∵EP⊥BD
∴∠APB=∠CPD
∵AB⊥BD,CD⊥BD
∴∠ABP=∠CDP=90°
∴△ABP∽△CDP
∴
∴
故选:A
5.B
解:如图,过作于 过作于
由小孔成像原理可得:
而
所以(cm),经检验符合题意.
故选B
6.C
解:如下图所示:
设AP=x,由题意可知:△COA∽△BPA,
∴,代入数据,,,
∴,解得,
∴所以人影扫过的面积是,
故选:C.
7.C
解:如下图所示:
∵AB∥A’B’,
∴△ABO∽△A’B’O,
∴,
由题意知:,代入上式中,
解得:.
故选:C.
8.B
解:如下图所示:
由题意可知:,
故有:,即,解得,
故选:B.
9.D
解:依题意,
cm,cm,m,m,
m
m
故选D
10.D
解:∵AB⊥BD,CD⊥BD,
∴∠ABO=∠CDO=90°,
又∵∠AOB=∠COD,
∴△ABO∽△CDO,
则,
∵AO=4m,AB=1.6m,CO=0.8m,
∴,
解得:CD=0.32m,
故选:D.
11.D
解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵∠B=90°,AB=4,BC=3,
∴AC=,
∵S△ABC=AB BC=AC BP,
∴BP=.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴.
设DE=x,则有:,
解得x=,
故选:D.
12.B
解:∵OA=3OD,OB=3CO,
∴OA:OD=BO:CO=3:1,∠AOB=∠DOC,
∴△AOB∽△DOC,
∴,
∴AB=3CD,
∵CD=4cm,
∴AB=12cm,
故选:B
13.A
解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=1m,FD=4m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴△EDC∽△FDC,
∴,即DC2=ED FD=1×4=4,
解得CD=2m.
故选A.
14.D
解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故选:D.
15. 相等 成比例 相似比 相似比 相似比的平方
解:略
16.6
解:,
;
,
,
;
设梯子AB的长为x米,
,
,即梯子的长度为6米.
故答案为:6
17.
解:如图,
∵北岸相邻的两根电线杆被南岸的5棵树遮挡住,
∴,,
∵,
∴,
,
∵,P到AB的距离即,
∴,
解得:,
∴河宽为36米,
故答案为:36.
18.27
解:∵,
∴,
∴,
即,
解得,
故井深为27尺.
故答案为:27
19.(1)不能看到高楼BD
(2)至少离高楼20米
(1)
解:不能看到高楼BD.
如图,连接PA并延长,交DB的延长线于点F
∵
∴在P点不能看到高楼BD.
(2)
解:至少离高楼为20米
设米
∵
∴
∴
∴
解得,经检验是分式方程的解
∴至少离高楼为20米.
20.(1)18m
(2)3.6m
解:(1)
如图1,
∵PMBD,
∴△APM∽△ABD,
,即,
∴AP=AB,
∵QB=AP,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)
如图2,他在路灯AC下的影子为BN,
∵BMAC,
∴△NBM∽△NAC,
∴,即,解得BN=3.6.
答:当他走到路灯BD时,他在路灯AC下的影长是3.6m.
21.步
解:由题意可知:,AH=15
∵H为GD的中点,K为DE的中点
DH=100,DK=100
∵AH∥DK
∴∠CDK=∠A
而∠CKD=∠AHD
∴
∴
即,
∴
答:出南门步恰好看到位于A处的树木.
22.(1)米
(2)设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即
(1)
解:标注点如下图:
根据题意在和,
,
,
,
分别为的中点,
,
,
(米);
(2)
解:设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即,过程如下:
根据题意作如下图形,
根据题意在和,
,
,
,
,
,
(米);
小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即即可.
23.(1)80cm;(2)
解:(1)∵当运动到点时,与重合于竖杆,
∴由题意可得;
(2)
如图,过点作于点,
,,
,
,
,
,
整理可得:.
答案第1页,共2页
