5.3.1函数的单调性(第一课时)课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(共23张PPT)
文档属性
| 名称 | 5.3.1函数的单调性(第一课时)课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 19:56:35 | ||
图片预览





文档简介
(共23张PPT)
5.3 导数的运算
5.3.1 函数的单调性
(第一课时)
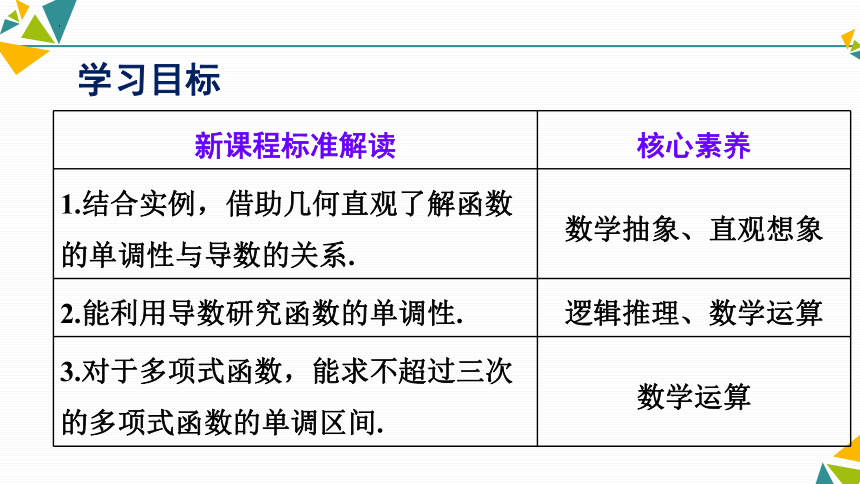
学习目标
新课程标准解读 核心素养
1.结合实例,借助几何直观了解函数的单调性与导数的关系. 数学抽象、直观想象
2.能利用导数研究函数的单调性. 逻辑推理、数学运算
3.对于多项式函数,能求不超过三次的多项式函数的单调区间. 数学运算
我们所学过的数学知识中刻画函数变化趋势(上升或下降的陡峭程度)的有哪些?
单调性
导数
探究新知
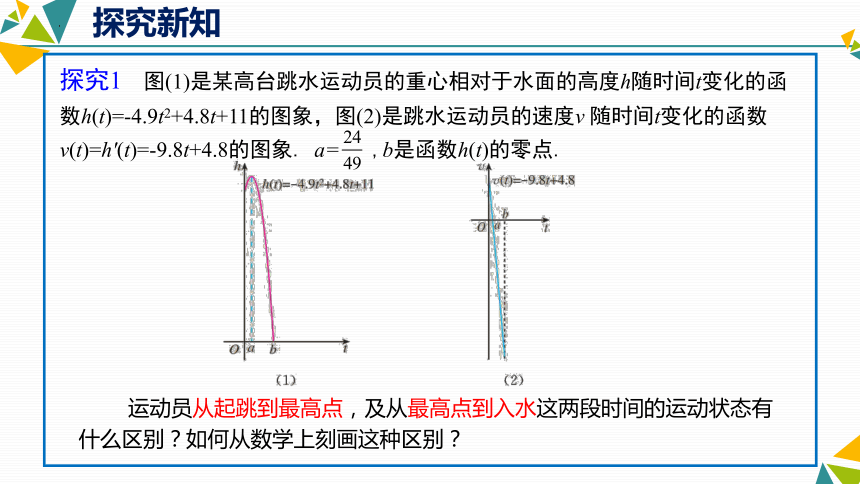
运动员从起跳到最高点,及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
探究1 图(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数h(t)=-4.9t2+4.8t+11的图象,图(2)是跳水运动员的速度v 随时间t变化的函数v(t)=h′(t)=-9.8t+4.8的图象. a= ,b是函数h(t)的零点.
探究新知
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)单调递增.相应地,v(t)=h′(t)>0.
(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度h随时间t的增加而减小,即h(t)单调递减.相应地,v(t)=h′(t)<0.
探究新知
问题1:能否由h′(t)的正负来判断函数h(t)的单调性呢?
在区间(a,b)上, h′(t)>0
在区间(a,b)上, h′(t)<0
在区间(a,b)上, h(t)单调递增
在区间(a,b)上, h(t)单调递减
猜想
对于高台跳水问题,可以发现:
当t∈(0,a)时,h′(t)>0,函数h(t)的图象是“上升”的,函数h(t)在(0,a)上单调递增;
当t∈(a,b)时,h′(t)<0,函数h(t)的图象是“下降”的,函数h(t)在(a,b)上单调递减.
探究新知
x
y
O
y=x
(1)
x
y
O
y=x2
(2)
x
y
O
y=x3
(3)
x
y
O
(4)
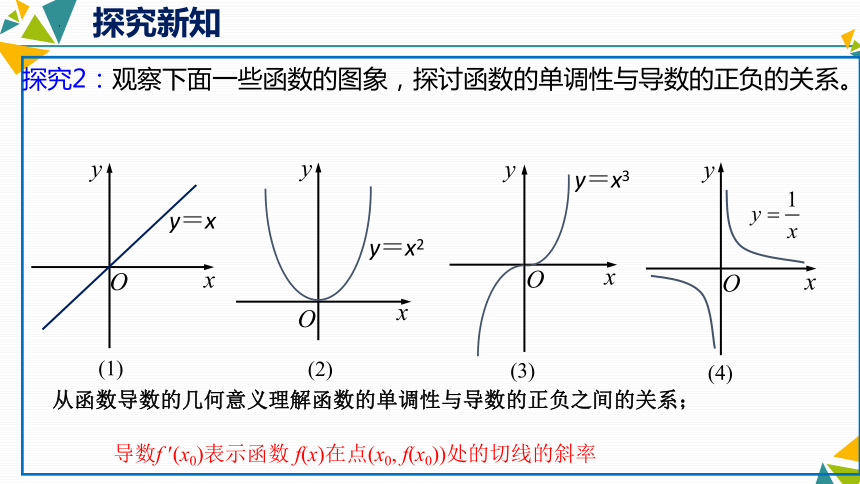
探究2:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系。
导数f (x0)表示函数 f(x)在点(x0, f(x0))处的切线的斜率
从函数导数的几何意义理解函数的单调性与导数的正负之间的关系;
探究新知
x
y
O
f (x)=x
(1)
x
y
O
f ′(x)=1
在(-∞, +∞)上, f (x)单调递增
在(-∞, +∞)上,f ′ (x)>0
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
x
y
O
f (x) =x2
(2)
x
y
O
f ′(x)=2x
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
探究新知
在(-∞, 0)上, f (x)单调递增
在(-∞, 0)上, f ′ (x)>0
x
y
O
f ′ (x) =3x2
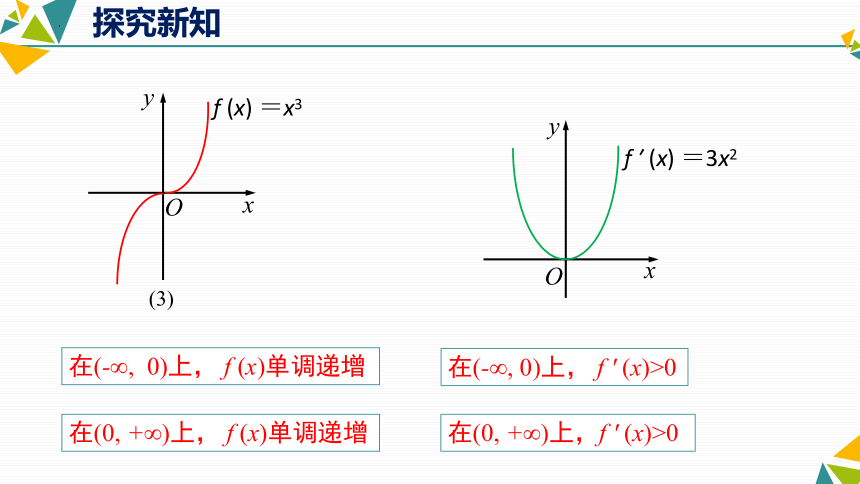
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
f (x) =x3
(3)
探究新知
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递减
在(0, +∞)上,f ′ (x)<0
x
y
O
(4)
x
y
O
f (x0)>0
f (x)在x0附近↗
切线“左下右上”
导数f ′(x0)
在区间上, f ′(x)>0
函数y=f (x)的图象在点(x0, f(x0))处切线的斜率
在x=x0处f ′(x0)>0
函数y=f (x)的图象上升,在x=x0附近单调递增
切线“左下右上”上升
在区间上,f (x) 单调递增
问题2:能否由h′(t)的正负来判断函数h(t)的单调性呢?
探究新知
问题2:能否由h′(t)的正负来判断函数h(t)的单调性呢?
探究新知
f (x1)<0
f (x)在x1附近↘
切线“左上右下”
导数f ′(x1)
在区间上, f ′(x)<0
函数y=f (x)的图象在点(x1, f(x1))处切线的斜率
在x=x1处f ′(x1)<0
函数y=f (x)的图象下降,在x=x1附近单调递减
切线“左上右下”下降
在区间上,f (x) 单调递减
定义形成
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,
在某个区间(a,b)上,如果f '(x)> 0,那么函数y=f(x) 在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f '(x)< 0,那么函数y=f(x) 在区间(a,b)上单调递减;
如果在某个区间内恒有 ,则 为常数.
定义剖析
例题精讲
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=.
解:(1)因为f(x)=x3+3x,
所以f '(x)=3x2+3=3(x2+1)>0.
所以,函数f(x)=x3+3x在R上单调递增,如图所示.
解: (2)因为f(x)=sinx-x,x∈(0,π),
所以f '(x)=cosx-1<0.
所以,函数f(x)=sinx-x在(0,π)上单调递减,如图所示.
例题精讲
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=.
解:(3)因为f(x)=, x∈(-∞,0)∪(0,+ ∞),所以f '(x)= >0.
所以,函数f(x)=在区间(-∞,0)和(0,+ ∞)上单调递增,如图所示
例题精讲
例2 已知导函数f '(x)的下列信息:
当10;当x<1,或x>4时, f '(x) <0;当x=1,或x=4时, f '(x)=0.
试画出函数f(x)图象的大致形状.
解:当10,可知f(x)在区间(1,4)上单调递增;
当x<1,或x>4时,f '(x)<0,可知f(x)在区间(-∞,1)和(4,+∞)上都单调递减;
当x=1,或x=4时,f '(x)=0,这两点比较特殊,我们称它们为“临界点”.
综上,函数f(x)图象的大致形状如图所示.
思考:请同学们回顾一下函数单调性的定义,并思考在某个区间上单调的函数y=f(x)的平均变化率的几何意义与f '(x)的正负的关系.
反馈练习
1.判断下列函数的单调性:
(1)f(x)=x2-2x+4;(2)f(x)=ex-x.
解: (1)因为f(x)=x2-2x+4是二次函数,其定义域为R.
所以其对称轴方程为x=1,又因为f(x)的图象开口向上,
所以,函数f(x)=x2-2x+4在(-∞,1)上单调递减,在(1,+∞)上单调递增.
解: (2)因为f(x)=ex-x ,其定义域为R.
所以f ′(x)=ex-1.
令f ′(x)= 0,得x=0
所以当x∈(-∞,0)时, f ′(x)<0
当x∈(0,+∞)时, f ′(x)>0 .
所以,函数f(x)=ex-x在(-∞,0)上单调递减,在(0,+∞)上单调递增.
反馈练习
2.函数y=f(x)的图象如图所示,
试画出函数y=f '(x)图象的大致形状.
解:由图可知,
当x∈(0,a)时,函数f (x)的图象没有升降,所以f ′(x)=0
当x∈(a,b)时,函数f (x)的图象是下降的,所以f ′(x)<0
当x∈(b,c)时,函数f (x)的图象没有升降,所以f ′(x)=0
反馈练习
反馈练习
小结反思
定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,
在某个区间(a,b)上,如果f '(x)> 0,那么函数y=f(x) 在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f '(x)< 0,那么函数y=f(x) 在区间(a,b)上单调递减;
如果在某个区间内恒有 ,则 为常数.
5.3 导数的运算
5.3.1 函数的单调性
(第一课时)
学习目标
新课程标准解读 核心素养
1.结合实例,借助几何直观了解函数的单调性与导数的关系. 数学抽象、直观想象
2.能利用导数研究函数的单调性. 逻辑推理、数学运算
3.对于多项式函数,能求不超过三次的多项式函数的单调区间. 数学运算
我们所学过的数学知识中刻画函数变化趋势(上升或下降的陡峭程度)的有哪些?
单调性
导数
探究新知
运动员从起跳到最高点,及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
探究1 图(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数h(t)=-4.9t2+4.8t+11的图象,图(2)是跳水运动员的速度v 随时间t变化的函数v(t)=h′(t)=-9.8t+4.8的图象. a= ,b是函数h(t)的零点.
探究新知
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)单调递增.相应地,v(t)=h′(t)>0.
(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度h随时间t的增加而减小,即h(t)单调递减.相应地,v(t)=h′(t)<0.
探究新知
问题1:能否由h′(t)的正负来判断函数h(t)的单调性呢?
在区间(a,b)上, h′(t)>0
在区间(a,b)上, h′(t)<0
在区间(a,b)上, h(t)单调递增
在区间(a,b)上, h(t)单调递减
猜想
对于高台跳水问题,可以发现:
当t∈(0,a)时,h′(t)>0,函数h(t)的图象是“上升”的,函数h(t)在(0,a)上单调递增;
当t∈(a,b)时,h′(t)<0,函数h(t)的图象是“下降”的,函数h(t)在(a,b)上单调递减.
探究新知
x
y
O
y=x
(1)
x
y
O
y=x2
(2)
x
y
O
y=x3
(3)
x
y
O
(4)
探究2:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系。
导数f (x0)表示函数 f(x)在点(x0, f(x0))处的切线的斜率
从函数导数的几何意义理解函数的单调性与导数的正负之间的关系;
探究新知
x
y
O
f (x)=x
(1)
x
y
O
f ′(x)=1
在(-∞, +∞)上, f (x)单调递增
在(-∞, +∞)上,f ′ (x)>0
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
x
y
O
f (x) =x2
(2)
x
y
O
f ′(x)=2x
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
探究新知
在(-∞, 0)上, f (x)单调递增
在(-∞, 0)上, f ′ (x)>0
x
y
O
f ′ (x) =3x2
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
f (x) =x3
(3)
探究新知
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递减
在(0, +∞)上,f ′ (x)<0
x
y
O
(4)
x
y
O
f (x0)>0
f (x)在x0附近↗
切线“左下右上”
导数f ′(x0)
在区间上, f ′(x)>0
函数y=f (x)的图象在点(x0, f(x0))处切线的斜率
在x=x0处f ′(x0)>0
函数y=f (x)的图象上升,在x=x0附近单调递增
切线“左下右上”上升
在区间上,f (x) 单调递增
问题2:能否由h′(t)的正负来判断函数h(t)的单调性呢?
探究新知
问题2:能否由h′(t)的正负来判断函数h(t)的单调性呢?
探究新知
f (x1)<0
f (x)在x1附近↘
切线“左上右下”
导数f ′(x1)
在区间上, f ′(x)<0
函数y=f (x)的图象在点(x1, f(x1))处切线的斜率
在x=x1处f ′(x1)<0
函数y=f (x)的图象下降,在x=x1附近单调递减
切线“左上右下”下降
在区间上,f (x) 单调递减
定义形成
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,
在某个区间(a,b)上,如果f '(x)> 0,那么函数y=f(x) 在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f '(x)< 0,那么函数y=f(x) 在区间(a,b)上单调递减;
如果在某个区间内恒有 ,则 为常数.
定义剖析
例题精讲
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=.
解:(1)因为f(x)=x3+3x,
所以f '(x)=3x2+3=3(x2+1)>0.
所以,函数f(x)=x3+3x在R上单调递增,如图所示.
解: (2)因为f(x)=sinx-x,x∈(0,π),
所以f '(x)=cosx-1<0.
所以,函数f(x)=sinx-x在(0,π)上单调递减,如图所示.
例题精讲
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=.
解:(3)因为f(x)=, x∈(-∞,0)∪(0,+ ∞),所以f '(x)= >0.
所以,函数f(x)=在区间(-∞,0)和(0,+ ∞)上单调递增,如图所示
例题精讲
例2 已知导函数f '(x)的下列信息:
当1
试画出函数f(x)图象的大致形状.
解:当1
当x<1,或x>4时,f '(x)<0,可知f(x)在区间(-∞,1)和(4,+∞)上都单调递减;
当x=1,或x=4时,f '(x)=0,这两点比较特殊,我们称它们为“临界点”.
综上,函数f(x)图象的大致形状如图所示.
思考:请同学们回顾一下函数单调性的定义,并思考在某个区间上单调的函数y=f(x)的平均变化率的几何意义与f '(x)的正负的关系.
反馈练习
1.判断下列函数的单调性:
(1)f(x)=x2-2x+4;(2)f(x)=ex-x.
解: (1)因为f(x)=x2-2x+4是二次函数,其定义域为R.
所以其对称轴方程为x=1,又因为f(x)的图象开口向上,
所以,函数f(x)=x2-2x+4在(-∞,1)上单调递减,在(1,+∞)上单调递增.
解: (2)因为f(x)=ex-x ,其定义域为R.
所以f ′(x)=ex-1.
令f ′(x)= 0,得x=0
所以当x∈(-∞,0)时, f ′(x)<0
当x∈(0,+∞)时, f ′(x)>0 .
所以,函数f(x)=ex-x在(-∞,0)上单调递减,在(0,+∞)上单调递增.
反馈练习
2.函数y=f(x)的图象如图所示,
试画出函数y=f '(x)图象的大致形状.
解:由图可知,
当x∈(0,a)时,函数f (x)的图象没有升降,所以f ′(x)=0
当x∈(a,b)时,函数f (x)的图象是下降的,所以f ′(x)<0
当x∈(b,c)时,函数f (x)的图象没有升降,所以f ′(x)=0
反馈练习
反馈练习
小结反思
定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,
在某个区间(a,b)上,如果f '(x)> 0,那么函数y=f(x) 在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f '(x)< 0,那么函数y=f(x) 在区间(a,b)上单调递减;
如果在某个区间内恒有 ,则 为常数.
