5.3.2函数的极值与最大(小)值课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(共18张PPT)
文档属性
| 名称 | 5.3.2函数的极值与最大(小)值课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 19:57:22 | ||
图片预览


文档简介
(共18张PPT)
5.3.2 函数的极值与最大(小)值
回顾:函数单调性与导数的关系:
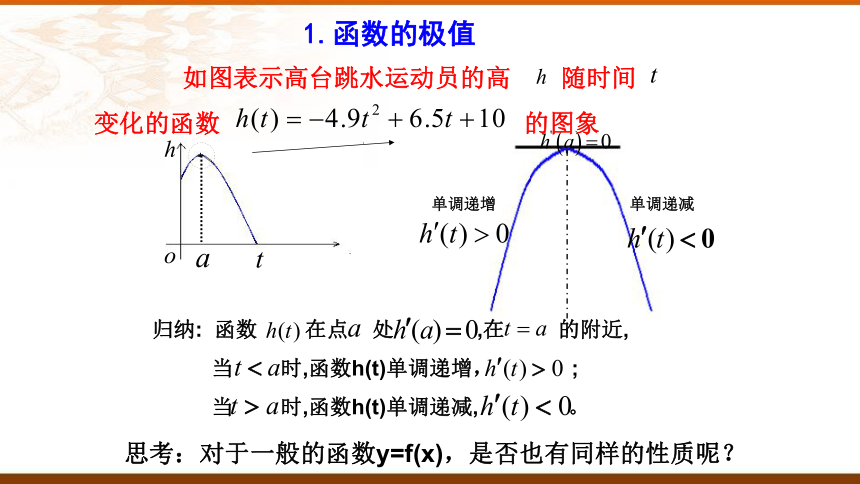
如图表示高台跳水运动员的高 随时间
变化的函数 的图象
单调递增
单调递减
归纳: 函数 在点 处 ,在 的附近,
当 时,函数h(t)单调递增, ;
当 时,函数h(t)单调递减, 。
思考:对于一般的函数y=f(x),是否也有同样的性质呢?
1.函数的极值
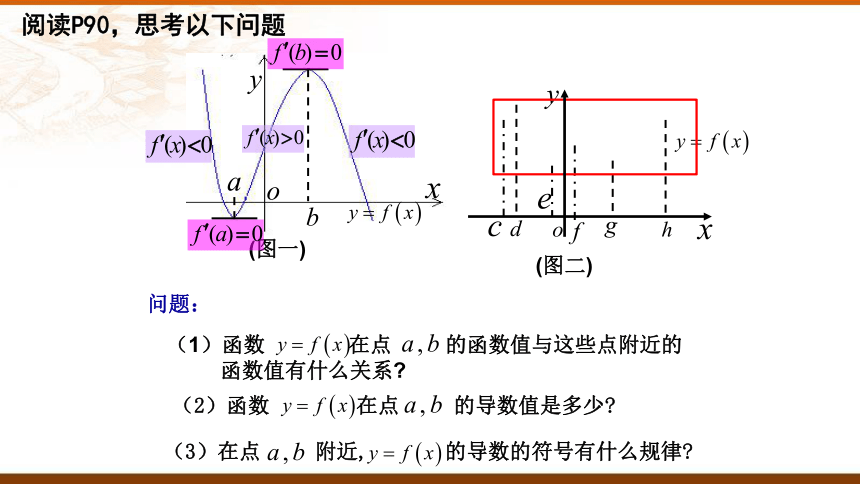
(3)在点 附近, 的导数的符号有什么规律
(1)函数 在点 的函数值与这些点附近的
函数值有什么关系
(2)函数 在点 的导数值是多少
(图一)
问题:
(图二)
阅读P90,思考以下问题
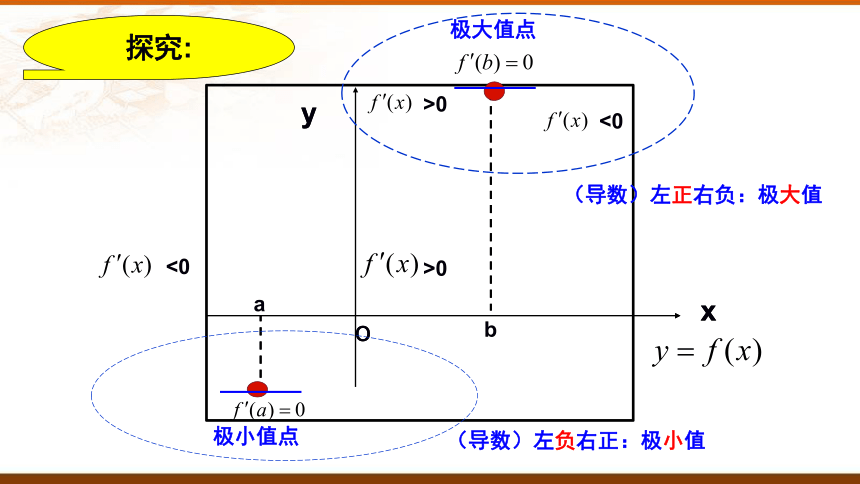
探究:
x
y
o
x
y
o
a
>0
<0
<0
>0
b
极小值点
极大值点
(导数)左正右负:极大值
(导数)左负右正:极小值
x
y
o
a
b
y=f(x)
f(a)
f(b)
x
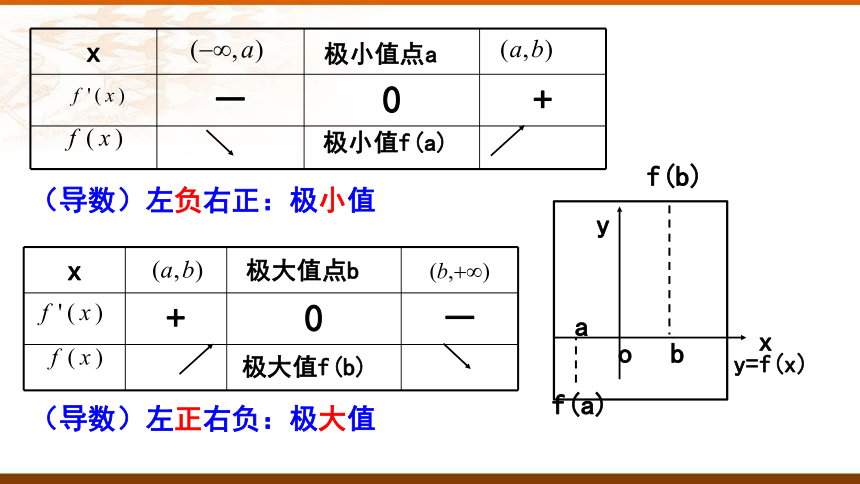
- 0 +
极小值f(a)
x
+ 0 -
极大值f(b)
极小值点a
极大值点b
(导数)左负右正:极小值
(导数)左正右负:极大值
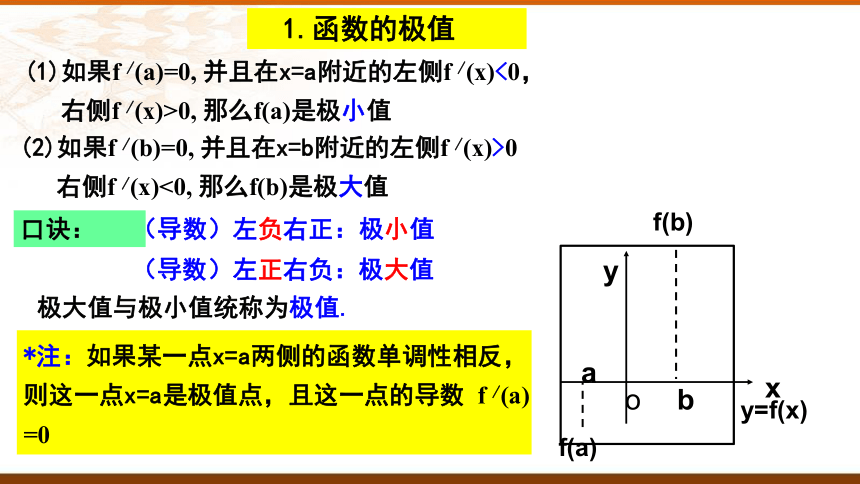
(2)如果f /(b)=0, 并且在x=b附近的左侧f /(x)>0
右侧f /(x)<0, 那么f(b)是极大值
1.函数的极值
(1)如果f /(a)=0, 并且在x=a附近的左侧f /(x)<0,
右侧f /(x)>0, 那么f(a)是极小值
(导数)左正右负:极大值
x
y
o
a
b
y=f(x)
f(a)
f(b)
(导数)左负右正:极小值
口诀:
极大值与极小值统称为极值.
*注:如果某一点x=a两侧的函数单调性相反,则这一点x=a是极值点,且这一点的导数 f /(a) =0
1.极大值一定大于极小值吗?
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值.
极小值
极大值
探究新知
思考
导数为0的点一定是函数的极值点吗?
o
x
y
+
+
例如:
不是
x0是函数f(x)的极值点
f′(x0)=0
x0是函数 f(x) 的极值点
x0左右两侧导数异号
f′(x0)=0
结论:f′(x0)=0 是可导函数在x0处取得极值的必要而不充分条件.
探究新知
2.若f′(x0)=0,则x0是否为极值点
x2, x4是函数f (x)的极值点,其中x2是极大值点,x4是极小值点.
追问:函数y=f′(x)的极大值点和极小值点分别是什么?
x1,x5是函数y=f′(x)的极大值点, x3,x6是函数y=f′(x)的极小值点.
1.函数y=f′(x)的图象如图所示,试找出函数f(x)的极值点,并指出哪些是极大值点,哪些是极小值点?
请看课本P92:练习1
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
f '(x) 0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
-2
O
x
y
2
令f′(x)=(x+2)(x-2)=0,解得x1=-2,x2=2
(导数)左正右负:极大值
(导数)左负右正:极小值
2.求下列函数的极值:
(2)f(x)=x3-27x; (3)f(x)=6+12x-x3.
解: (2)函数f (x)的定义域为R,且 f′(x)=3x2-27.
令f′(x)=0,得x=±3
所以, f (x)在x=-3时取得极大值, 且极大值为f (-3)=54;
f (x)在x=3时取得极小值, 且极小值为f (3)=-54.
(3) 同理可得,f (x)在x=-2时取得极小值, 且极小值为f (-2)= -10;
f (x)在x=2时取得极大值, 且极大值为f (2)=22.
当x变化时,f′(x)与 f(x)的变化情况如下表:
x (–∞, –3) –3 (–3, 3) 3 ( 3, +∞)
f '(x) 0 0
f (x) 54 -54
–
+
+
单调递增
单调递减
单调递增
请看课本P92:练习2
(导数)左正右负:极大值
(导数)左负右正:极小值
x (0, e) e (e, +∞)
f ′(x) + 0 -
f (x)
当x变化时,f′(x)与f(x)的变化情况如下表:
单调递增
单调递减
因此,x=e是函数的极大值点,极大值为f(e)= ,没有极小值.
解:函数 的定义域为 (0,+∞),且 .
补充练习
令f′(x)=0,解得x=e.
练习2:函数f(x)=alnx+bx2+x在x=1和x=2处有极值,求a、b的值
解:
因为函数在x=1和x=2处有极值,
所以在x=1和x=2处导数为0
*注:如果某一点x=a两侧的函数单调性相反,则这一点x=a是极值点 ,且这一点的导数 f /(a) =0
2.函数的最大(小)值
函数在闭区间[a,b]上的最值:
1.如果函数在区间[a,b]上的图象是一条连续不断的曲线,那么函数必有最大值和最小值
2.最大值一定比最小值大.
3.函数的最值通常在极值点或区间端点处取得
4.只要把函数的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值。
一般地,利用导数求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(2)将y=f(x)的各极值与端点处函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1)求f(x)在区间(a,b)内的极值(极大值或极小值)
5.3.2 函数的极值与最大(小)值
回顾:函数单调性与导数的关系:
如图表示高台跳水运动员的高 随时间
变化的函数 的图象
单调递增
单调递减
归纳: 函数 在点 处 ,在 的附近,
当 时,函数h(t)单调递增, ;
当 时,函数h(t)单调递减, 。
思考:对于一般的函数y=f(x),是否也有同样的性质呢?
1.函数的极值
(3)在点 附近, 的导数的符号有什么规律
(1)函数 在点 的函数值与这些点附近的
函数值有什么关系
(2)函数 在点 的导数值是多少
(图一)
问题:
(图二)
阅读P90,思考以下问题
探究:
x
y
o
x
y
o
a
>0
<0
<0
>0
b
极小值点
极大值点
(导数)左正右负:极大值
(导数)左负右正:极小值
x
y
o
a
b
y=f(x)
f(a)
f(b)
x
- 0 +
极小值f(a)
x
+ 0 -
极大值f(b)
极小值点a
极大值点b
(导数)左负右正:极小值
(导数)左正右负:极大值
(2)如果f /(b)=0, 并且在x=b附近的左侧f /(x)>0
右侧f /(x)<0, 那么f(b)是极大值
1.函数的极值
(1)如果f /(a)=0, 并且在x=a附近的左侧f /(x)<0,
右侧f /(x)>0, 那么f(a)是极小值
(导数)左正右负:极大值
x
y
o
a
b
y=f(x)
f(a)
f(b)
(导数)左负右正:极小值
口诀:
极大值与极小值统称为极值.
*注:如果某一点x=a两侧的函数单调性相反,则这一点x=a是极值点,且这一点的导数 f /(a) =0
1.极大值一定大于极小值吗?
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值.
极小值
极大值
探究新知
思考
导数为0的点一定是函数的极值点吗?
o
x
y
+
+
例如:
不是
x0是函数f(x)的极值点
f′(x0)=0
x0是函数 f(x) 的极值点
x0左右两侧导数异号
f′(x0)=0
结论:f′(x0)=0 是可导函数在x0处取得极值的必要而不充分条件.
探究新知
2.若f′(x0)=0,则x0是否为极值点
x2, x4是函数f (x)的极值点,其中x2是极大值点,x4是极小值点.
追问:函数y=f′(x)的极大值点和极小值点分别是什么?
x1,x5是函数y=f′(x)的极大值点, x3,x6是函数y=f′(x)的极小值点.
1.函数y=f′(x)的图象如图所示,试找出函数f(x)的极值点,并指出哪些是极大值点,哪些是极小值点?
请看课本P92:练习1
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
f '(x) 0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
-2
O
x
y
2
令f′(x)=(x+2)(x-2)=0,解得x1=-2,x2=2
(导数)左正右负:极大值
(导数)左负右正:极小值
2.求下列函数的极值:
(2)f(x)=x3-27x; (3)f(x)=6+12x-x3.
解: (2)函数f (x)的定义域为R,且 f′(x)=3x2-27.
令f′(x)=0,得x=±3
所以, f (x)在x=-3时取得极大值, 且极大值为f (-3)=54;
f (x)在x=3时取得极小值, 且极小值为f (3)=-54.
(3) 同理可得,f (x)在x=-2时取得极小值, 且极小值为f (-2)= -10;
f (x)在x=2时取得极大值, 且极大值为f (2)=22.
当x变化时,f′(x)与 f(x)的变化情况如下表:
x (–∞, –3) –3 (–3, 3) 3 ( 3, +∞)
f '(x) 0 0
f (x) 54 -54
–
+
+
单调递增
单调递减
单调递增
请看课本P92:练习2
(导数)左正右负:极大值
(导数)左负右正:极小值
x (0, e) e (e, +∞)
f ′(x) + 0 -
f (x)
当x变化时,f′(x)与f(x)的变化情况如下表:
单调递增
单调递减
因此,x=e是函数的极大值点,极大值为f(e)= ,没有极小值.
解:函数 的定义域为 (0,+∞),且 .
补充练习
令f′(x)=0,解得x=e.
练习2:函数f(x)=alnx+bx2+x在x=1和x=2处有极值,求a、b的值
解:
因为函数在x=1和x=2处有极值,
所以在x=1和x=2处导数为0
*注:如果某一点x=a两侧的函数单调性相反,则这一点x=a是极值点 ,且这一点的导数 f /(a) =0
2.函数的最大(小)值
函数在闭区间[a,b]上的最值:
1.如果函数在区间[a,b]上的图象是一条连续不断的曲线,那么函数必有最大值和最小值
2.最大值一定比最小值大.
3.函数的最值通常在极值点或区间端点处取得
4.只要把函数的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值。
一般地,利用导数求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(2)将y=f(x)的各极值与端点处函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1)求f(x)在区间(a,b)内的极值(极大值或极小值)
